Duplicate

Lecture 3 | Projective Geometry II

수강 일자
2023/02/22

Intersection of Lines: Examples

l=(−1,0,1)T→x=1l′=(0,−1,1)T→y=1{\rm l} = (-1,0,1)^T \rarr x=1\\ {\rm l'} = (0, -1, 1)^T \rarr y=1
•
두 선의 intersection 은 cross product 로 계산할 수 있음.
l×l′=(1,1,1)T{\rm l} \times {\rm l'} = (1, 1,1)^T

Intersection of Two Parallel Lines

l=(−1,0,1)T→−x+1=0l′=(0,−1,1)T→−x+2=0l′′=(−1,0,c)T→−x+c=0{\rm l} = (-1,0,1)^T \rarr -x +1=0\\ {\rm l'} = (0, -1, 1)^T \rarr -x+2=0 \\ {\rm l''} = (-1,0,c)^T \rarr -x +c=0\\
•
두 선 l,l′{\rm l}, {\rm l'} 의 intersection 은 cross product 로 계산할 수 있음.
l×l′=(0,1,0)T{\rm l} \times {\rm l'} = (0,1,0)^T
◦
Ideal Point (Infinity) 에서 교차하는 것을 알 수 있음.
•
임의의 cc 값을 가지는 l′′{\rm l''} 은 모두 (0,1,0)(0,1,0) 을 지남.
◦
(−1,0,c)T(0,1,0)=0(-1,0,c)^T(0,1,0) = 0 이기 때문에, 임의의 cc 값을 가지는 l′′{\rm l ''} 은 (0,1,0)T(0,1,0)^T 을 지나고 이 점에서 교차함을 알 수 있음.

Ideal Points and Line at Infinity

•
Ideal Point 는 일반적으로 다음과 같이 표현됨.
(x1,x2,0)T(x_1,x_2,0)^T
•
모든 Ideal Point 는 Line at Infinity 위에 있음.
l∞=(0,0,1)T{\rm l}_{\infty}=(0,0,1)^T
◦
Proof: (0,0,1)T(x1,x2,0)=0(0,0,1)^T(x_1,x_2,0)=0

Intersection of a Line and l∞{\rm l}_{\infty}

l=(a,b,c)Tl∞=(0,0,1)T{\rm l} = (a,b,c)^T \\ {\rm l}_{\infty} = (0,0,1)^T
•
두 선의 교차점은 cross product 로 구할 수 있음.
l×l∞=(b,−a,0)T{\rm l }\times {\rm l}_{\infty} = (b, -a ,0)^T
◦
cc 와는 무관함. → 방향만 상관 있음. (사실, 방향의 비율만 상관 있는게, 어차피 비율이 같은 점은 Homogeneous Coordinate 에서 같은 점이기 때문임…)

The Beauty of Projective Space P2{\mathbb{P}}^2

•
두 distinct line 은 하나의 점에서 만남.
•
두 선이 평행인지 아닌지에 따라서 연산 및 판단 등에 구별을 두지 않음.
•
Finite Point 와 Ideal Point 를 동일한 형태로 표현할 수 있음.

Duality

l=x×x′=[x]×x′x=l×l′=[l]×l′l⋅x=lTx=0{\rm l} = {\rm x} \times {\rm x'}= [{\rm x}]_{\times}{\rm x'} \\ {\rm x} = {\rm l} \times {\rm l'}= [{\rm l}]_{\times}{\rm l'} \\ {\rm l} \cdot {\rm x} = {\rm l}^T {\rm x} = 0
•
선과 점에 대한 구별이 무의미한 연산 식들임.
◦
Duality Principle: 선과 점의 역할을 바꾸어도 식이 모두 성립함. (Indistinguishable)

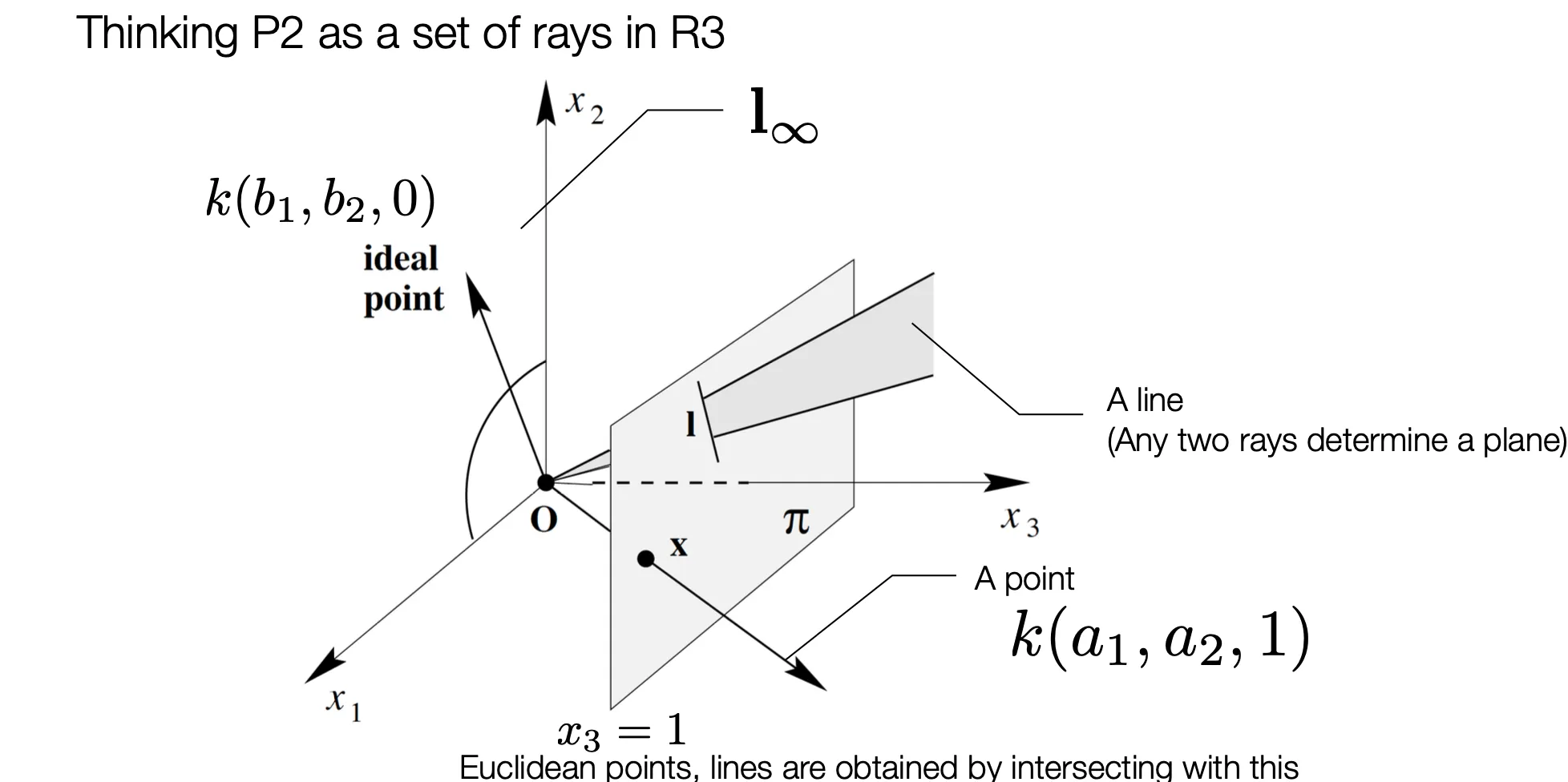
Relation between Projective Space and Camera Projection Model

•
Projection Space P2{\mathbb P}^2 상의 point 는 Euclidean Space R3{\mathbb R}^3 상의 ray 에 대응됨.
•
세 번째 항이 1 인 점은 Euclidean Space R3{\mathbb R}^3 상에서 x3=1x_3=1 인 plane 이자, Projection Space P2{\mathbb P}^2 에서는 전체 도메인임. (Image Plane)
•
Euclidean Space R3{\mathbb R}^3 에서 ray 상의 점들을 Image Plane 상으로 projection 을 하는 행위는 ray 상의 점들을 같은 점으로 변환시키는 행위가 되고, 곧 Euclidean Space R3{\mathbb R}^3 를 Projection Space P2{\mathbb P}^2 로 표현하는 과정임.

Conic

ax2+bxy+cy2+dx+ey+f=0ax^2+bxy+cy^2+dx+ey+f=0
•
Homogeneous Coordinate 로 표현하기 위해 y→x2x3,x→x1x3y \to \frac{x_2}{x_3}, x \to \frac{x_1}{x_3} 으로 변환할 수 있음.
ax12+bx1x2+cx22+dx1x3+ex2x3+fx32=0ax_1^2 + bx_1x_2+cx_2^2 + dx_1x_3+ex_2x_3+fx_3^2 = 0
•
위 식은 Matrix Multiplication form 으로 변환할 수 있음.
(x1,x2,x3)[ab/2d/2b/2ce/2d/2e/2f](x1x2x3)(x_1,x_2,x_3) \begin{bmatrix} a & b/2 & d/2 \\ b/2 & c & e/2 \\ d/2 & e/2 & f \end{bmatrix} \begin{pmatrix} x_1 \\ x_2\\ x_3 \end{pmatrix}
◦
Homogeneous Coordinate 에서 line equation 을 계수로 표현한 것과 같이, Conic 은 위 matrix form 의 가운데 matrix CC 로 나타냄.
◦
CC 는 symmetric matrix.
◦
Homogeneous Coordinate 자체가 Up-to-Scale 이기 때문에 CC 도 Up-to-Scale 임.
◦
CC 는 a,b,c,d,e,fa,b,c,d,e,f 여섯 개의 변수가 존재하지만, Up-to-Scale 이므로 5DoF 임.
◦
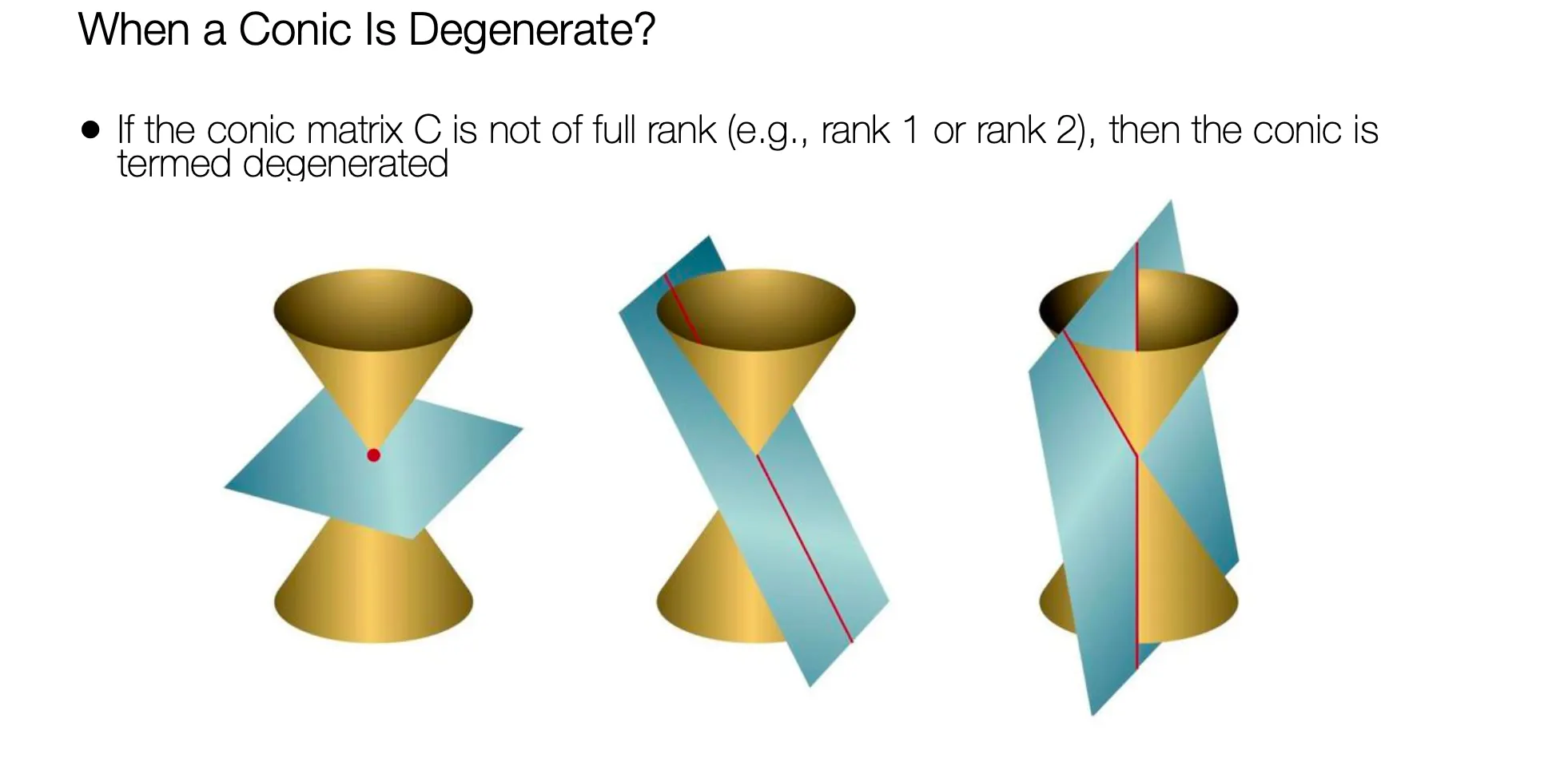
CC 는 full rank 가 아닐 수도 있음. (degenerated case)
•
다섯 개의 점이 Conic Equation 의 다섯 변수를 결정함.
axi2+bxiyi+cyi2+dxi+eyi+f=0→[xi2xiyiyi2xiyi1][abcdef]=0→[x12x1y1y12x1y11x22x2y2y22x2y21x32x3y3y32x3y31x42x4y4y42x4y41x52x5y5y52x5y51][abcdef]=0ax_i^2+bx_iy_i+cy_i^2 +dx_i+ey_i+f = 0 \\ \to \begin{bmatrix} x_i^2 & x_iy_i & y_i^2 & x_i & y_i & 1 \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \end{bmatrix} = 0 \\ \to \begin{bmatrix} x_1^2 & x_1y_1 & y_1^2 & x_1 & y_1 & 1 \\ x_2^2 & x_2y_2 & y_2^2 & x_2 & y_2 & 1 \\ x_3^2 & x_3y_3 & y_3^2 & x_3 & y_3 & 1 \\ x_4^2 & x_4y_4 & y_4^2 & x_4 & y_4 & 1 \\ x_5^2 & x_5y_5 & y_5^2 & x_5 & y_5 & 1 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \end{bmatrix} = 0
◦
SVD 를 이용해 Ax=0Ax=0 을 만족하는 non-zero solution xx 를 찾을 수 있음.

Circle

•
Conic Equation 에서 a=ca=c 이고 b=0b=0 인 특수한 경우임.
axi2+ayi2+dxi+eyi+f=0→[x12+y12x1y11x22+y22x2y21x32+y32x3y31][adef]=0ax_i^2 + ay_i^2 + dx_i +ey_i +f = 0 \\ \to \begin{bmatrix} x_1^2 + y_1^2 & x_1 & y_1 & 1 \\ x_2^2 + y_2^2 & x_2 & y_2 & 1 \\ x_3^2 + y_3^2 & x_3 & y_3 & 1 \end{bmatrix} \begin{bmatrix} a \\ d \\ e \\ f \end{bmatrix} = 0
◦
Up-to-Scale 에 의해 3DoF 가 됨.

Tangent Lines to Conics

•
Conic CC 위의 점 x{\rm x} 에서의 Tangent Line 은 다음과 같이 표현할 수 있음.
l=Cx{\rm l } = C{\rm x}
◦
x{\rm x} 가 unique 하다는 가정 하에서 다음과 같이 증명할 수 있음.
lTx=(Cx)Tx=xTCTx=xTCx=0{\rm l}^T {\rm x} = (C{\rm x})^T{\rm x} = {\rm x}^TC^T{\rm x} = {\rm x}^T C {\rm x} = 0
◦
만약 l{\rm l} 과 CC 의 또 다른 교차점 yy 가 존재한다면, CC 는 그냥 line 임. (degnerated case)
lTy=0yTCy=0xTCy=(Cx)Ty=lTy=0yTCx=yTl=0{\rm l}^T {\rm y} = 0 \quad {\rm y}^TC{\rm y} = 0 \\ {\rm x}^T C{\rm y} = (C{\rm x})^T{\rm y}={\rm l}^T {\rm y} = 0 \\ {\rm y}^T C{\rm x} = y^T{\rm l} = 0 \\
▪
xTCx=xTCy=yTCx=yTCy=0{\rm x}^TC{\rm x} = {\rm x}^TC{\rm y} = {\rm y}^TC{\rm x} = {\rm y}^TC{\rm y} = 0 이므로 다음이 성립함.
(x+αy)TC(x+αy)=0({\rm x} + \alpha{\rm y})^TC({\rm x} + \alpha{\rm y}) = 0
▪
즉, x{\rm x} 와 y{\rm y} 사이를 잇는 직선 위 모든 점이 Conic Equation 을 만족함. → Line 이 Conic 이자, degenerated case 임.

Degenerate Conics

•
Two Intersecting Lines
x2−y2=0→(x+y)(x−y)=0x^2-y^2 = 0 \to (x+y)(x-y) = 0
◦
Homogeneous Coordinate 로는 두 선 l,m{\rm l}, {\rm m} 에 대해 다음과 같음.
C=lmT+mlTC={\rm l}{\rm m}^T + {\rm m}{\rm l}^T
▪
증명은 다음과 같음.
xTCx=xT(lmT+mlT)x=(xTl)(mTx)+(xTm)(lTx){\rm x}^TC{\rm x} = {\rm x}^T({\rm l}{\rm m}^T + {\rm m}{\rm l}^T ){\rm x} = ({\rm x}^T{\rm l})({\rm m}^T {\rm x}) + ({\rm x}^T m )({\rm l}^T {\rm x})
•
l{\rm l} 위의 점 x{\rm x} 에 대해서 lTx=0{\rm l}^T{\rm x}=0 이기 때문에 xTCx=0{\rm x}^TC{\rm x} =0
•
m{\rm m} 위의 점 x{\rm x} 에 대해서 mTx=0{\rm m}^T{\rm x}=0 이기 때문에 xTCx=0{\rm x}^TC{\rm x} =0{}
•
A Point
x2=0x^2 = 0

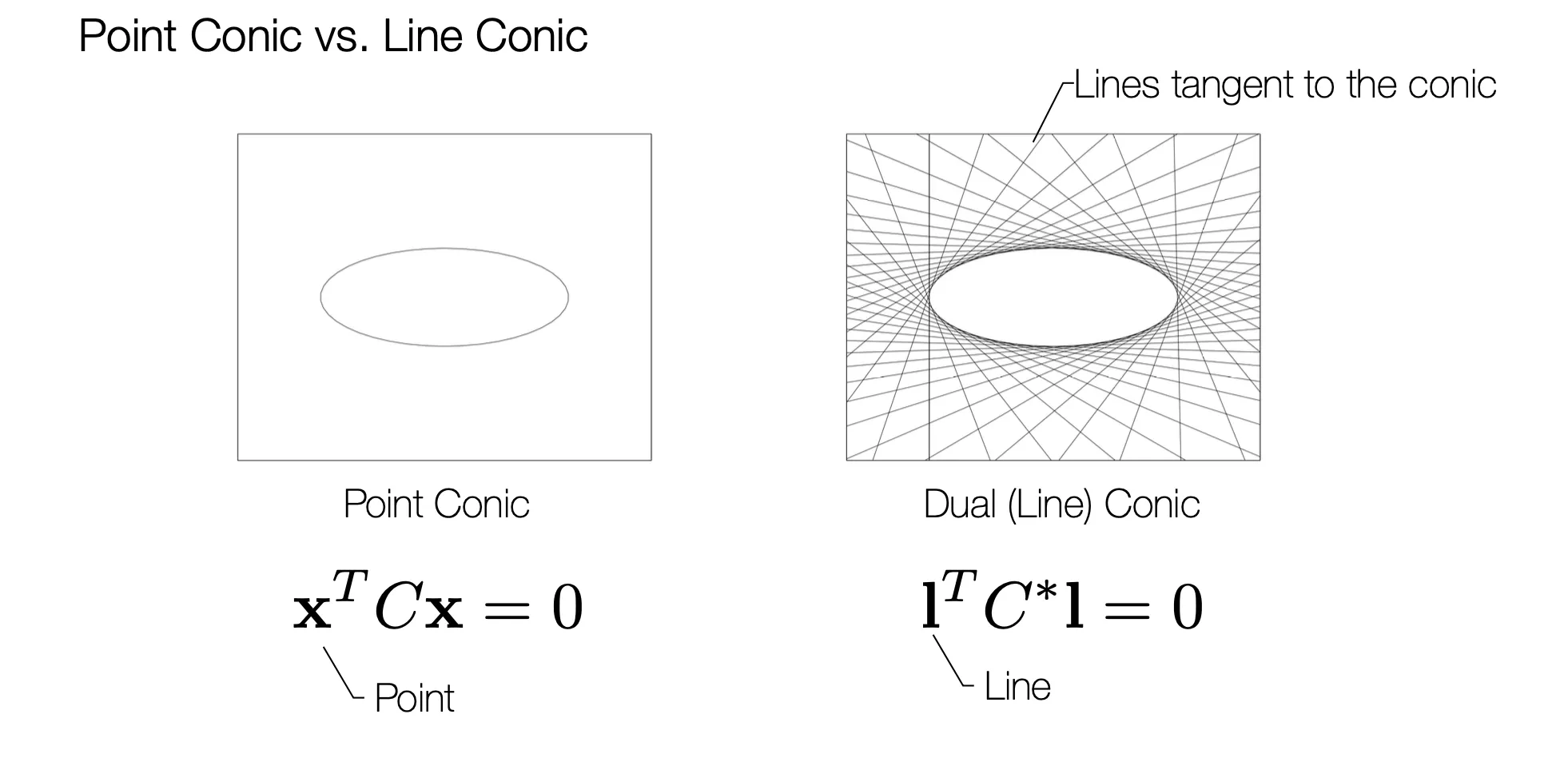
Dual Conic

•
Homogeneous Coordinate 는 기본적으로 Duality 가 존재함.
•
Conic Equation 을 만족하는 3차원 벡터가 Point 일 것이나 Line 일 것이냐에 따라서 Point Conic 과 Dual Conic 으로 나누어짐.
•
일반적으로 Line Conic 의 CC 와 Dual Conic 의 C∗C^* 은 inverse 관계임. (동일한 것을 표현하기 위해)
l=Cx→C−1l=xxTCx=(C−1l)TC(C−1l)=lTC−TCC−1l=lTC−Tl=lTC−1l=0{\rm l} = C{\rm x} \to C^{-1}{{\rm l}} = {\rm x}\\ \quad \\ \begin{align*} {\rm x}^TC{\rm x} &= (C^{-1}{\rm l})^TC(C^{-1}{\rm l}) \\ &= {\rm l}^TC^{-T}CC^{-1}{\rm l} \\ &={\rm l}^TC^{-T}{\rm l} \\ &={\rm l}^TC^{-1}{\rm l} = 0 \end{align*}