Duplicate

Lecture 2 | Linear Algebra Review

형태
Math
수강 일자
2022/09/07
기본적인 내용은 정리하지 않았습니다. (ex. Vector, Matrix, Matrix Multiplication, etc.)

Hadamard Product (Element-wise Product)

(A∘B)ij=(A⊙B)ij=(A)ij(B)ij(A \circ B)_{ij} = (A \odot B)_{ij} = (A)_{ij}(B)_{ij}

Trace

trA=∑i=1nAii{\rm tr}A = \sum_{i=1}^n A_{ii}
•
대각 성분의 합
•
trA=trAT{\rm tr}A = {\rm tr}A^T
•
tr(A+B)=trA+trB{\rm tr}(A+B) = {\rm tr}A + {\rm tr}B
•
tr(tA)=ttrA{\rm tr}(tA) = t {\rm tr}A
•
tr(AB)=tr(BA){\rm tr}(AB) = {\rm tr}(BA) where ABAB is square
•
tr(ABC)=tr(BCA)=tr(CAB){\rm tr}(ABC) ={\rm tr}(BCA) = {\rm tr}(CAB) where ABCABC is square

Norms

∥x∥p=(∑i=1n∣xi∣p)1/p\|x\|_p = (\sum_{i=1}^n |x_i|^p)^{1/p}
•
vector 의 각 항을 non-negative 로 변경해주는 함수
•
Intuitive 하게는 origin 으로부터 xx 까지의 거리를 측정하는 함수
•
f(x)=0→x=0f(x)=0 \rarr x=0
•
f(x+y)≤f(x)+f(y)f(x+y) \le f(x)+f(y) (the triangular inequality)
•
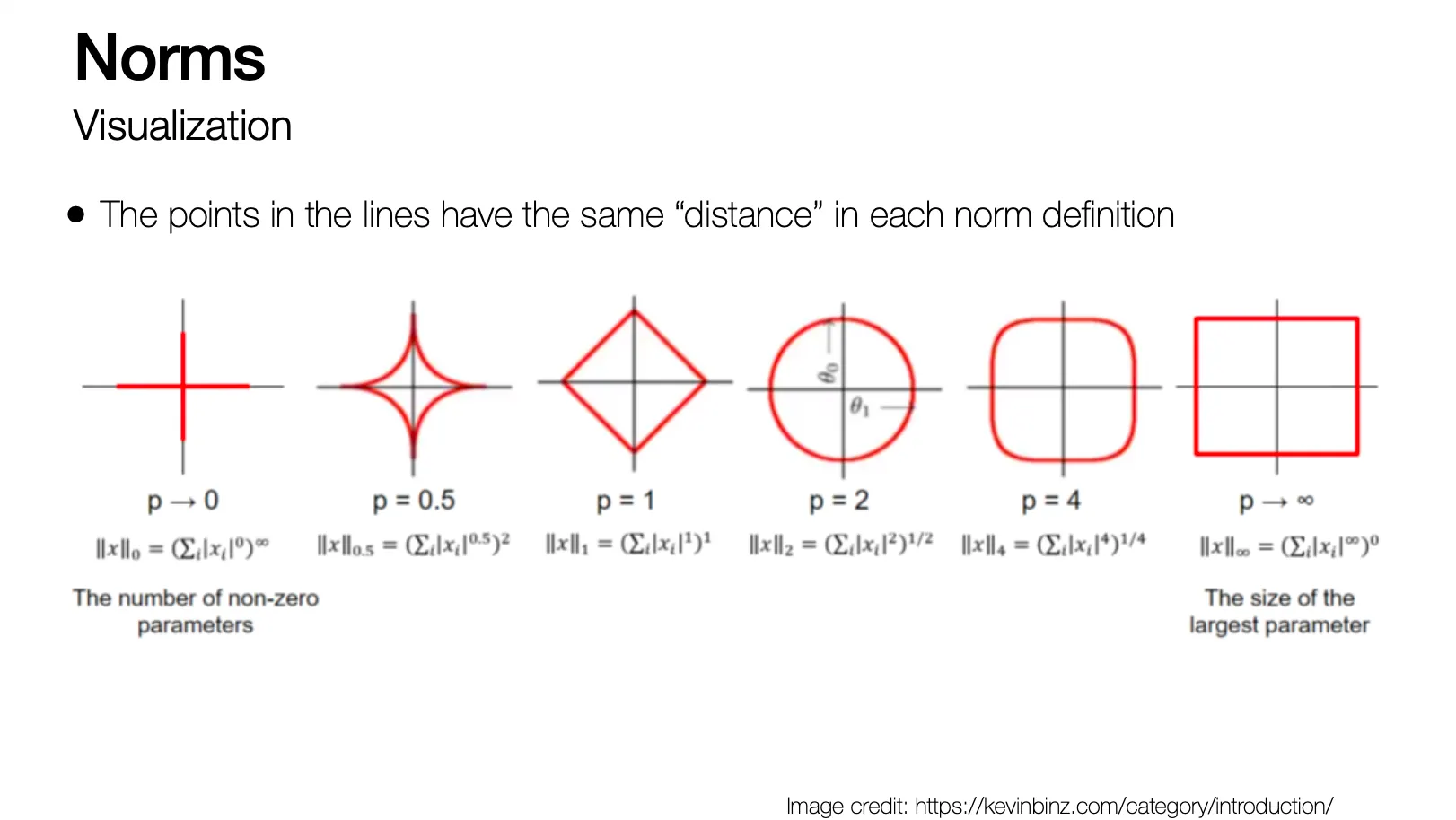
∀α∈R\forall \alpha \in \mathbb R , f(αx)=∣α∣f(x)f(\alpha x) = |\alpha | f(x)
•
Norm 의 종류
◦
Euclidean (L2 norm)
∥x∥2=∑i=1nxi2\|x\|_2 = \sqrt{\sum_{i=1}^n x_i^2}
◦
L1 norm
∥x∥1=∑i=1n∣xi∣\|x\|_1 = \sum_{i=1}^n |x_i|
◦
L-infinity norm
∥x∥∞=max⁡i∣xi∣\|x\|_\infty = \max_i |x_i|
◦
L0 norm: non-zero element 의 개수
◦
Frobenius norm (matrix norm)
∥A∥F=∑i=1m∑j=1nAij2=tr(AAT)\|A\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n A_{ij}^2} = \sqrt{{\rm tr}(AA^T)}
▪
보통 두 matrix 의 similarity 를 계산하는데 사용됨
•
Visualization of Norms

Linear Dependence and Independence

•
Vector 의 set {x1,x2,⋯ ,xn}\{x_1,x_2, \cdots, x_n \} 은 set 내의 어떤 한 벡터를 골라도 나머지 벡터들의 linear combination 으로 표현될 수 없을 때 이 linearly independent 라고 함

Rank of a Matrix

•
Column Rank 는 matrix A∈Rm×nA \in \mathbb R^{m\times n} 의 linearly independent 한 largest column subset 의 크기
•
Row Rank 는 matrix A∈Rm×nA \in \mathbb R^{m\times n} 의 linearly independent 한 largest row subset 의 크기
•
모든 matrix A∈Rm×nA \in \mathbb R^{m\times n} 에 대해서 Row Rank 와 Column Rank 는 동일하고 이를 Rank of AA, rank(A){\rm rank}(A) 라고 지칭함
•
∀A∈Rm×n\forall A\in \mathbb R^{m\times n} 에 대해 rank(A)≤min⁡(m,n){\rm rank}(A) \le \min(m,n)
•
∀A∈Rm×n,B∈Rn×p\forall A\in \mathbb R^{m\times n}, B \in \mathbb R^{n\times p} 에 대해 rank(AB)≤min⁡(rank(A),rank(B)){\rm rank}(AB) \le \min({\rm rank}(A),{\rm rank}(B))
•
∀A,B∈Rm×n\forall A, B\in \mathbb R^{m\times n} 에 대해 rank(A+B)≤rank(A)+rank(B){\rm rank}(A+B) \le {\rm rank}(A) +{\rm rank}(B)

Inverse of a Square Matrix

A−1A=I=AA−1A^{-1}A = I =AA^{-1}
•
Matrix multiplication 을 행했을 때 Identitiy 가 되는 matrix
•
A−1A^{-1} 가 존재하면 AA 를 invertible 혹은 non-singular 라고 함
•
A−1A^{-1} 가 존재하기 위해서는 AA 가 full rank 를 가져야 함
•
(A−1)−1=A(A^{-1})^{-1} = A
•
(AB)−1=B−1A−1(AB)^{-1} = B^{-1}A^{-1}
•
(A−1)T=(AT)−1(A^{-1})^T= (A^T)^{-1}

Span and Projection

•
Vector set {x1,x2,...,xn}\{ x_1, x_2, ..., x_n\} 의 span 은 해당 벡터들의 linear combination 으로 표현할 수 있는 모든 벡터의 set 임
span({x1,x2,...,xn})={v:v=∑i=1nαixi,    αi∈R}{\rm span}(\{ x_1, x_2, ..., x_n\}) = \{v:v = \sum_{i=1}^n \alpha_i x_i, \thickspace\thickspace\alpha_i \in\mathbb R \}
•
Vector yy 의 span of {x1,x2,...,xn}\{ x_1, x_2, ..., x_n\} 에 대한 projection 은 v∈span({x1,x2,...,xn})v \in{\rm{span}}(\{ x_1, x_2, ..., x_n\}) 이면서 yy 와의 euclidean norm 이 가장 작은 벡터 vv
Proj(y:{x1,x2,...,xn})=arg min⁡v∈span({x1,x2,...,xn})∥y−v∥2{\rm Proj}(y:\{ x_1, x_2, ..., x_n\}) = \argmin_{v \in {\rm{span}}(\{ x_1, x_2, ..., x_n\})} \|y-v\|_2

Orthogonal Matricies

•
두 벡터 x,yx, y 는 xTy=0x^Ty = 0 이면 orthogonal 하다고 부름
•
벡터 xx 는 ∥x∥2=1\|x\|_2 = 1 이면 normalized 되었다고 부름
•
Square matrix U∈Rn×nU \in \mathbb R^{n\times n} 은 모든 column 이 서로 다른 column 과 orthogonal 일 때 orthogonal 하다고 부름. 각 column 이 normalized 까지 되어있으면 orthonormal 이라고 부름.
•
UTU=I=UUTU^T U = I = UU^T
•
∥Ux∥2=∥x∥2\|Ux\|_2 = \|x\|_2 (Orthonormal matrix 와의 matrix multiplication 은 norm 을 유지)

Rotation Matrix

R=[cos⁡θ−sin⁡θ−sin⁡θcos⁡θ]R = \begin{bmatrix} \cos\theta & -\sin\theta \\ -\sin\theta & \cos\theta \\ \end{bmatrix}
•
RR 은 orthonormal matrix
•
det(R)=1{\rm det}(R) = 1