Duplicate

Lecture 12 | Calibration Triangulation

형태
Computer Vision
수강 일자
2022/10/12

Extrinsic Parameters

•
Real World coordinate 를 카메라마다의 위치에 맞게 camera coordinate 로 변경해주는 작업이 필요함 → Rotation + Translation
Xcam=RXworld+t=[R ∣ t][Xworld1]{\rm X_{cam}} = R{\rm X_{world}}+{\rm t} = [R\ |\ {\rm t}]\begin{bmatrix} \rm X_{world} \\ 1 \end{bmatrix}
◦
Ccam=(0,0,0)T=RCworld+t→Cworld=−RTt{\rm C_{cam}} = (0,0,0)^T = R{\rm C_{world} + t} \rarr {\rm C_{world} } = -R^T \rm t
•
Extrinsic: World coordinate → Camera coordinate
•
Intrinsic: 3D → 2D
•
Camera Calibration: obtaining K,R,t\rm K,R,t
•
x1=K1[R1 ∣ t1]Xworld{\rm x_1} = K_1[{\rm R_1\ |\ t_1}]\rm X_{world}, x2=K2[R2 ∣ t2]Xworld{\rm x_2} = K_2[{\rm R_2\ |\ t_2}]\rm X_{world} …

Cameras at Infinity: Affine Camera

•
카메라가 물체와 굉장히 먼 거리가 떨어져 있을 때 (z>>Δz)z >> \Delta z)
•
Depth 에 대한 정보가 의미가 없을 정도로 거리가 멀어 본래 거리가 가까울 수록 크고 멀수록 작았던 perspective effect 가 사라짐! → parallel line 이 parallel 함
•
Finite Camera (Perspective)
P=[m11m12m13t1m21m22m23t2m31m32m331]P=\begin{bmatrix} m_{11} & m_{12} & m_{13} & t_1 \\ m_{21} & m_{22} & m_{23} & t_2 \\ m_{31} & m_{32} & m_{33} & 1 \\ \end{bmatrix}
•
Affine Camera
PA=[m11m12m13t1m21m22m23t20001]P_A=\begin{bmatrix} m_{11} & m_{12} & m_{13} & t_1 \\ m_{21} & m_{22} & m_{23} & t_2 \\ 0 & 0 & 0& 1 \\ \end{bmatrix}
◦
Affine
◦
Weak Perspective
◦
(scaled) Orthographic
◦
Parallel line 이 여전히 parallel 함 (Affine Transform)
◦
zz 가 커지면 Weak Perspective (이미 엄청 큰 d0d_0 와 그에 비해 작은 Δ\Delta 가 있을 때, d0+Δd_0+\Delta 의 위치의 obejct 를 그냥 d0d_0 의 projection 으로 가정해버림) 와 Perspective 의 차이가 0 에 한없이 가까워짐!
•
Orthographic Projection
x=[100001000001]X=[XY1]\rm x = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}X = \begin{bmatrix} X \\ Y \\ 1 \\ \end{bmatrix}
◦
Scaled Orthographic Projection
x=[α0000α000001]X=[αXαY1]\rm x = \begin{bmatrix} \alpha & 0 & 0 & 0 \\ 0 & \alpha & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}X = \begin{bmatrix} \alpha X \\ \alpha Y \\ 1 \\ \end{bmatrix}
•
Weak Perspective Projection
x=[αx0000αy000001]X=[αxXαyY1]\rm x = \begin{bmatrix} \alpha_x & 0 & 0 & 0 \\ 0 & \alpha_y & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}X = \begin{bmatrix} \alpha_x X \\ \alpha_y Y \\ 1 \\ \end{bmatrix}
•
Affine Projection
x=[αxs000αy000001]X=[αxX+sYαyY1]\rm x = \begin{bmatrix} \alpha_x & s & 0 & 0 \\ 0 & \alpha_y & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}X = \begin{bmatrix} \alpha_x X + sY \\ \alpha_y Y \\ 1 \\ \end{bmatrix}

Camera Calibration

•
Goal 은 K,R,t\rm K, R, t (P\rm P) 를 찾는 것
•
크게 두 가지 방법 (1) Direct Linear Transform 과 (2) Zhang’s Method 이 있음

Direct Linear Tranform(DLT) for Camera Calibration

•
Homography 를 estimate 할 때 사용했던 방법과 사실상 동일함
xi=[P11P12P13P14P21P22P23P24P31P32P33P34]Xi\rm x_i = \begin{bmatrix} P_{11} & P_{12} & P_{13} & P_{14} \\ P_{21} & P_{22} & P_{23} & P_{24} \\ P_{31} & P_{32} & P_{33} & P_{34} \\ \end{bmatrix}X_i
[XiYiZi1−xiXi−xiYi−xiZi−xiXiYiZi1−yiXi−yiYi−yiZi−yi][P11P12P13P14P21P22P23P24P31P32P33P34]=02×1\begin{bmatrix} X_i & Y_i & Z_i & 1 & & & & & -x_iX_i & -x_iY_i & -x_iZ_i & -x_i \\ & & & & X_i & Y_i & Z_i & 1 & -y_iX_i & -y_iY_i & -y_iZ_i & -y_i \end{bmatrix} \begin{bmatrix} P_{11} \\ P_{12} \\ P_{13} \\ P_{14} \\ P_{21} \\ P_{22} \\ P_{23} \\ P_{24} \\ P_{31} \\ P_{32} \\ P_{33} \\ P_{34} \\ \end{bmatrix} = 0_{2\times1}
◦
DoF 가 11 이기 때문에 6 개의 coreesponding points 가 필요함
◦
즉, 알려진 3D structure 를 두고 이미지를 찍은 뒤, corresponding point 들을 찾고 DLT 를 해결함
•
하지만, PP 는 3D 를 2D 로 변환하는 matrix 이지 world coordinate 를 Camera coordinate 로 바꿔주는 matrix 는 아님 → PP 로부터 K,R,t\rm K, R, t 를 뽑아내는 과정이 필요함!

Decomposition of the Camera Matrix

•
Ccam=(0,0,0)T=RCworld+t→Cworld=−RTt{\rm C_{cam}} = (0,0,0)^T = R{\rm C_{world} + t} \rarr {\rm C_{world} } = -R^T \rm t
•
P=K[R ∣ t]=K[R ∣ −RCworld]=[KR ∣ −KRCworld]P=K[{\rm R}\ |\ {\rm t}] = K[{\rm R}\ |\ -{\rm R}{\rm C_{world}}] = [K{\rm R}\ |\ -K{\rm R}{\rm C_{world}}]
•
Cworld{\rm C_{world}} 구하기
◦
PCworld=K(RCworld+t)=0P{\rm C_{world}} = K({\rm RC_{world} +t}) = 0 이므로, Cworld{\rm C_{world}} 는 PP 의 null space 로 구할 수 있음! (SVD 사용)
•
KK, R\rm R 구하기
◦
PP 의 좌측 3×33\times3 은 KRK \rm R 이므로, PP 의 left 3×33\times3 를 RQ Decomposition 을 하여 각각의 KK, R\rm R 을 구해냄
◦
RQ Decomposition 의 결과로 나오는 Q 는 orthogonal, R 은 upper triangular matrix 로, R\rm R 이 orthogonal 이고 KK 가 upper triangle 이라는 점이 완벽히 일치함
•
t\rm t 구하기
◦
t=−RCworld{\rm t} = -R {\rm C_{world}} 로 구함

Zhang’s Method

•
실제 상황에서 3D pattern 을 준비하는 것은 어려움.
•
Checkerboard 같은 2D pattern 을 준비하는 것이 훨씬 많이 사용됨!

Epipolar Geometry

•
두 calibrated 된 camera pose 에서 하나의 object 를 촬영하는 상황에서 두 camera center 와 object 지점은 coplanar 라는 평면을 이룸

Triangulation

•
Multiview 에서 촬영한 이미지를 기반으로 3D 를 reconstruction 하려는 시도를 생각해볼 수 있음!
•
Reconstruction 을 하려면 물체가 움직이지 않아야 함, 만약 움직인다면 두 카메라가 synchronized 되어 있어서 동시에 이미지를 찍으면 reconstruction 가능함
•
Camera center 에서 이미지의 corresponding point 로 ray 를 쏘면 한 지점 XX 에서 만날 것을 기대할 수 있음.
◦
실제로는 잘 안되기 때문에 각각의 ray 위에 최대한 놓이는 것을 목표로 구해낼 수 있음!
◦
아래는 3D 지점 X\rm X 가 camera 1 에 의해서 x1\rm x_1 에 맺힌 상황을 나타낸 것임
▪
x1=(x1,y1,1)T{\rm x_1} = (x_1, y_1, 1)^T
x1=P1X=[p11Tp12Tp13T]X\rm x_1 = P_1X = \begin{bmatrix} {p_1^1}^T \\ {p_1^2}^T \\ {p_1^3}^T \\ \end{bmatrix}X
x1≡P1X→λx1=P1X→x1×P1X=0\rm x_1 \equiv P_1X \rarr \lambda x_1=P_1X \rarr x_1 \times P_1X = 0
◦
최종적으로 외적 연산을 풀면 다음과 같은 수식이 나옴
x1(p13TX)−p11TX=0y1(p13TX)−p12TX=0x1(p12TX)−y1p11TX=0x_1({p_1^3}^T{\rm X})-{p_1^1}^T{\rm X} = 0 \\ y_1({p_1^3}^T{\rm X})-{p_1^2}^T{\rm X} = 0 \\ x_1({p_1^2}^T{\rm X})-y_1{p_1^1}^T{\rm X} = 0
[x1(p13T)−p11Ty1(p13T)−p12T]X=0\begin{bmatrix} x_1({p_1^3}^T) - {p_1^1}^T \\ y_1({p_1^3}^T) - {p_1^2}^T \\ \end{bmatrix} \rm X =0
◦
위처럼 하나의 view 마다 2×42\times 4 와 4×14\times 1 의 곱셈 형태로 식을 만들 수 있음
◦
X\rm X 는 3 DoF 이므로 2 개의 view 가 있으면 X\rm X 를 찾아낼 수 있음!

Non-linear Optimization

•
Triangularization 에서 실제로 원하는 것은 구해낸 3D point 를 다시 reprojection 했을 때의 상의 error 가 최소화가 되는 3D point 임
X∗=arg min⁡X∑i∥πi(X)−xi∥22X^* = \argmin_X \sum_i \| \pi_i({\rm X}) - {\rm x}_i \|_2^2
∥πi(X)−xi∥22=(Pi1XPi3X−xi)2+(Pi2XPi3X−yi)2\| \pi_i({\rm X}) - {\rm x}_i \|_2^2 = (\frac{{\rm P}_i^1 {\rm X}}{{\rm P}_i^3 {\rm X}} - x_i)^2 + (\frac{{\rm P}_i^2 {\rm X}}{{\rm P}_i^3 {\rm X}} - y_i)^2
•
DLT 만으로도 가능하지만 (Algebraic Error 만 고려) DLT 로 initialize 하고 reprojection error 를 줄이는 방향으로 optimize 를 계속 해나가야 함! (ex. gradient descent)

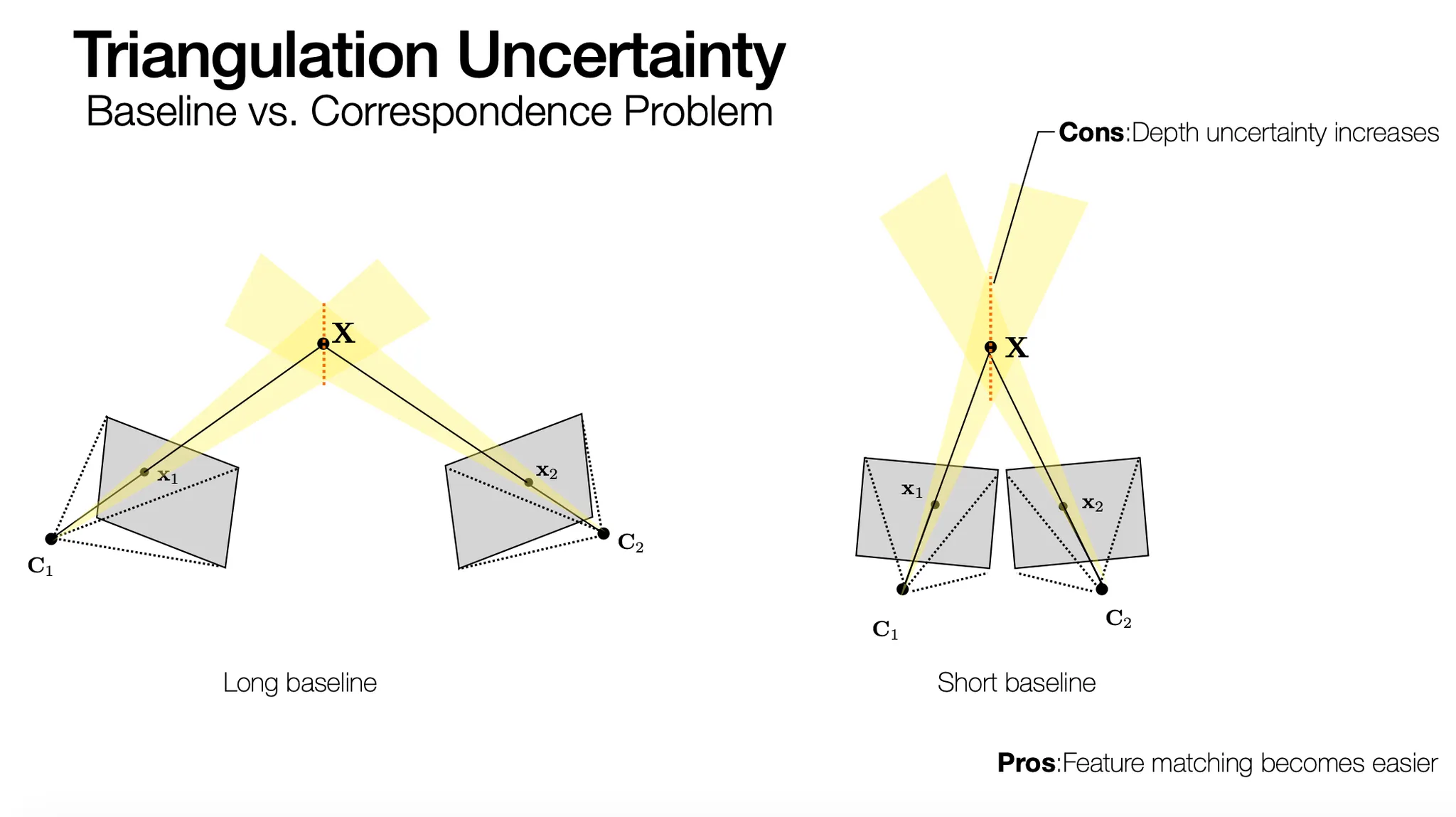
Triangluation Uncertainty

•
3D reconstruction 에서 long baseline 이 좋을까 short baseline 이 좋을까?
•
Long Baseline
◦
Pros: 같은 2D plane 상의 error 더라도 depth uncertainty 가 낮기 때문에 reconstruction 이 덜 noisy 함 → Short Baseline 의 Cons
◦
Cons: Feature Matching 을 찾는 것이 어려움 → Short Baseline 의 Pros

Perspective-n-Point (PnP)

•
3D 와 2D 의 corresponding 이 주어졌을 때 camera pose (R,t\rm R, t) 를 찾는 문제
•
KK 는 주어졌다고 가정함 (calibrated camera)
•
모델이 주어졌고, camera location 을 찾을 때 사용됨!

Structure-from Motion

•
이미지만 가지고 3D 를 재구성할 수 있음
•
각각의 시간 때에 K,R,tK, R, t 가 자동적으로 계산됨 → 3D point 가 triangulation 으로 계산됨
•
Photo Tourism
◦
엄청 많은 이미지를 인터넷에서 모으고, correspondence 를 SIFT 등으로 구하고 matching 을 시킨 후에 camera calibration 을 하고 3D reconstruction 을 함!