Duplicate

Lecture 5 | Edge Detection

수강 일자
2022/09/21

Edge Detection

•
Edge 는 Image Brightness (혹은 grayscale 값) 이 급격하게 변하 (거나 불연속성이 존재하)는 Line Segment 임.
•
Edge Detection 을 통해 이미지 상에서 눈에 뜨는 feature 를 추출할 수 있고, 픽셀 형태의 이미지를 가지고 있는 것보다 계산적으로 효율적인 경우가 많음.
•
사람의 시각 시스템의 visual cortex 에서 가장 앞에 있는 부분이 V1 cell 이라고 알려져 있는데 이 부분에서도 가장 먼저 하는 일이 Edge Detection 임.

Origin of Edges

•
Edge 가 생기는 이유는 다양함.
1.
Suface Normal 의 불연속성
2.
Depth 의 불연손성 (object 의 boundary 에서 관측자와 보이는 것과의 거리가 급격히 바뀌는 지점)
3.
Surface Color 이 불연속성 (ex. 약병의 글씨)
4.
Illumniation 의 불연속성 (조명 조건이 급격하게 변하는 영역)

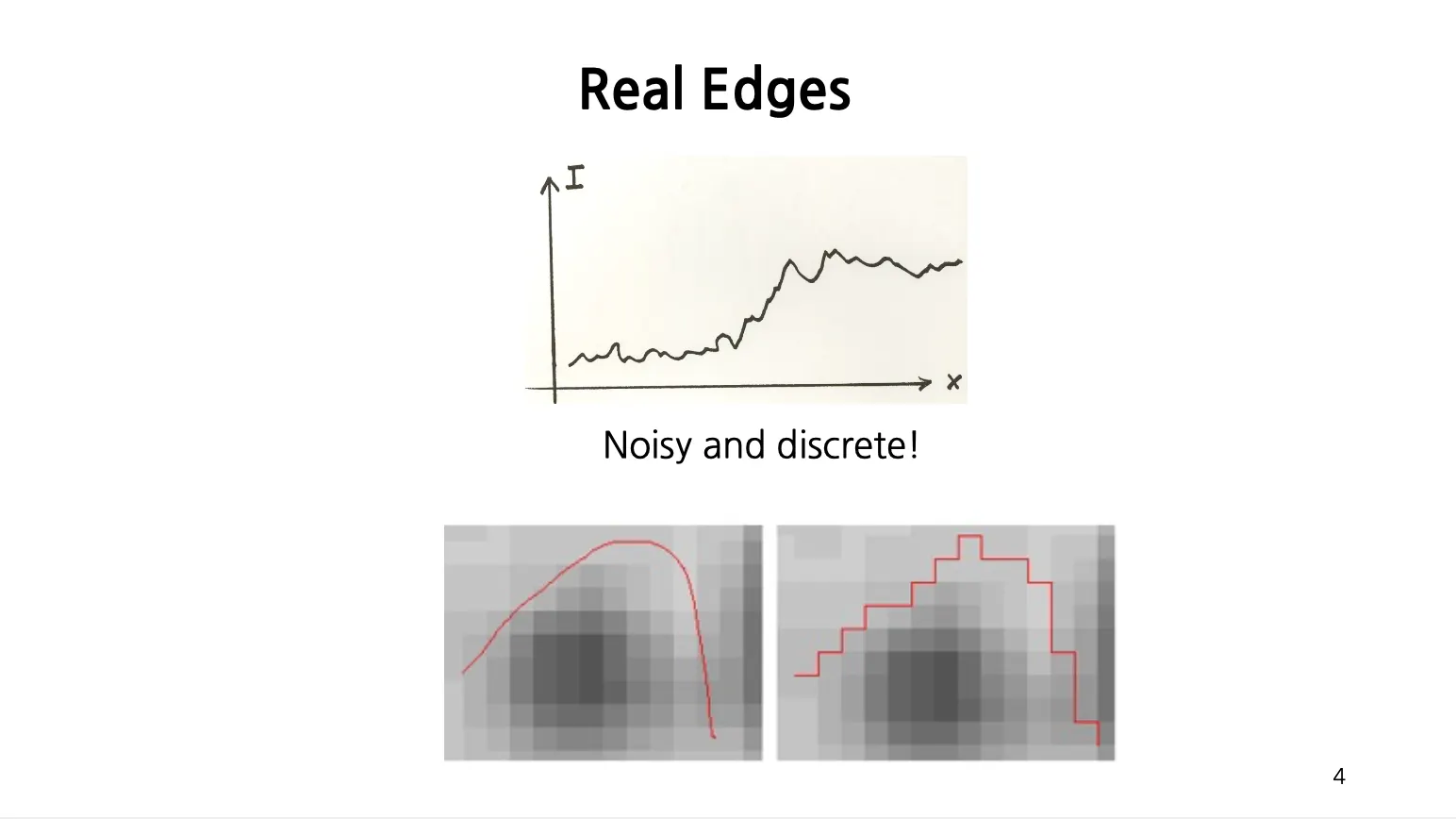
Real Edges

•
실제로 이미지 상에서 점으로 표현되어 있는 부분도 확대하여 보면 noisy 하고 discrete 하게 표현된 픽셀의 조합으로 나타남.
◦
때문에 정확한 Edge Detection 을 하는 것은 쉬운 문제는 아님.
•
Edge 를 정의하기 위해 다음과 같은 세 개의 Edge Operator 를 만들어 볼 수 있음.
◦
Edge Magnitude
▪
얼마나 Edge 가 강한 값인가-
▪
같은 흰색으로 표현된 Edge 라도 완전 흰색은 픽셀값이 급격하게 변하는 부분이고, 회색빛이 있는 부분은 픽셀값이 서서히 변하는 부분임.
◦
Edge Orientation
▪
어느 방향으로 Edge 가 존재하는가-
◦
High Detection Rate & Good Localization
▪
어느 부분에 Edge 가 있는가- 얼마나 실제와 같은 위치에 Edge 가 존재하는가 (좋은 Localization 을 보이는가-)

Gradient

•
Gradient Equation
∇f=[∂f∂x,∂f∂y]\nabla f =[\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}]
•
Gradient Direction
arctan⁡(∂f∂y/∂f∂x)\arctan(\frac{\partial f}{\partial y} / \frac{\partial f}{\partial x})
•
Gradient Magnitude
∥∇f∥=(∂f∂x)2+(∂f∂y)2\|\nabla f \|=\sqrt {(\frac{\partial f}{\partial x})^2 + (\frac{\partial f}{\partial y})^2}

Discrete Edge Operators

•
Discrete 한 이미지를 어떻게 미분하여 Edge 를 구할 것인가?
∂I∂x≈12ϵ((Ii+1,j+1−Ii,j+1)+(Ii+1,j−Ii,j))∂I∂y≈12ϵ((Ii+1,j+1−Ii+1,j)+(Ii,j+1−Ii,j))\frac{\partial I}{\partial x} \approx \frac{1}{2\epsilon} ((I_{i+1,j+1}-I_{i,j+1})+(I_{i+1,j}-I_{i,j})) \\ \frac{\partial I}{\partial y} \approx \frac{1}{2\epsilon} ((I_{i+1,j+1}-I_{i+1,j})+(I_{i,j+1}-I_{i,j}))
◦
Convolution Masks
∂I∂x≈12ϵ(−11−11)∂I∂y≈12ϵ(11−1−1)\frac{\partial I}{\partial x} \approx \frac{1}{2\epsilon} \begin{pmatrix} -1 & 1 \\ -1 & 1 \end{pmatrix} \\ \frac{\partial I}{\partial y} \approx \frac{1}{2\epsilon} \begin{pmatrix} 1 & 1 \\ -1 & -1 \end{pmatrix}
•
Second Order Partial Derivatives
∂2I∂x2≈1ϵ2(Ii−1,j−2Ii,j+Ii+1,j)∂2I∂y2≈1ϵ2(Ii,j−1−2Ii,j+Ii,j+1)\frac{\partial^2 I}{\partial x^2} \approx \frac{1}{\epsilon^2} (I_{i-1,j}-2I_{i,j}+I_{i+1,j}) \\ \frac{\partial^2 I}{\partial y^2} \approx \frac{1}{\epsilon^2} (I_{i,j-1}-2I_{i,j}+I_{i,j+1})
•
Laplacian
∇2I=∂2I∂x2+∂2I∂y2\nabla^2 I = \frac{\partial^2 I}{\partial x^2} + \frac{\partial^2 I}{\partial y^2}
◦
Convolution Masks
∇2I≈1ϵ2(0101−41010)\nabla^2 I \approx \frac{1}{\epsilon^2} \begin{pmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{pmatrix}\\
◦
Convolution Masks (More Accurate)
∇2I≈1ϵ2(1111−81111)\nabla^2 I \approx \frac{1}{\epsilon^2} \begin{pmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end{pmatrix}
▪
사선의 방향도 고려

The Sobel Operators

•
Gradient 를 구하는 또다른 방법인데, 사실 정답이 존재하기 보다는 사선의 변화를 얼마나 고려할 것인가- 등의 요소들로 구별하여 다른 것들을 사용해볼 수 있음.
•
Sobel Operators for partial x
(−101−202−101)=(121)×(−101) \begin{pmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \times \begin{pmatrix} -1 & 0 & 1 \end{pmatrix}
◦
y 방향으로는 gaussian, x 방향으로는 differentiate
•
Sobel Operators for partial y
(121000−1−2−1)=(10−1)×(121) \begin{pmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} \times \begin{pmatrix} 1 & 2 & 1 \end{pmatrix}
◦
y 방향으로는 differentiate, x 방향으로는 gaussian

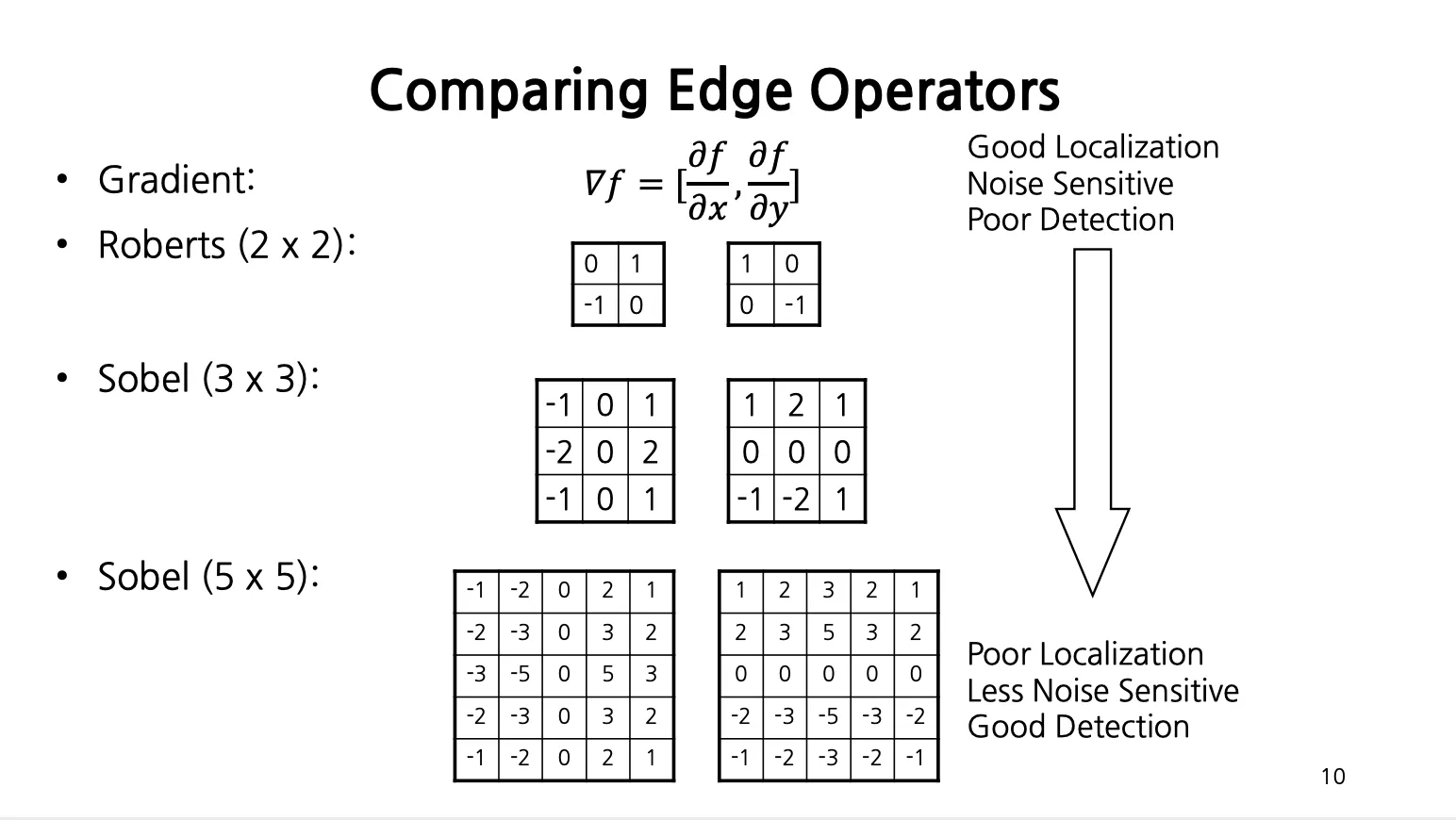
Comparing Edge Operators

•
Graient 를 어떻게 구하느냐에 따라서 다양한 Edge Operator 들이 존재
•
작은 Operator 는 실제 변화량이 있는 국소 부분에 대한 detection 이 가능하기 때문에 localization 이 좋지만 noise 가 많을 경우에 이를 감지 및 증폭하여 detection rate 가 떨어질 수 있음.
•
큰 Operator 는 넓은 영역을 보기 때문에 국소 부분에 대한 detection 이 떨어지고 localization 이 안좋지만, noise sensitiviy 는 좋아짐.
•
대중적으로 Sobel (3×33\times 3) 가 많이 사용됨.

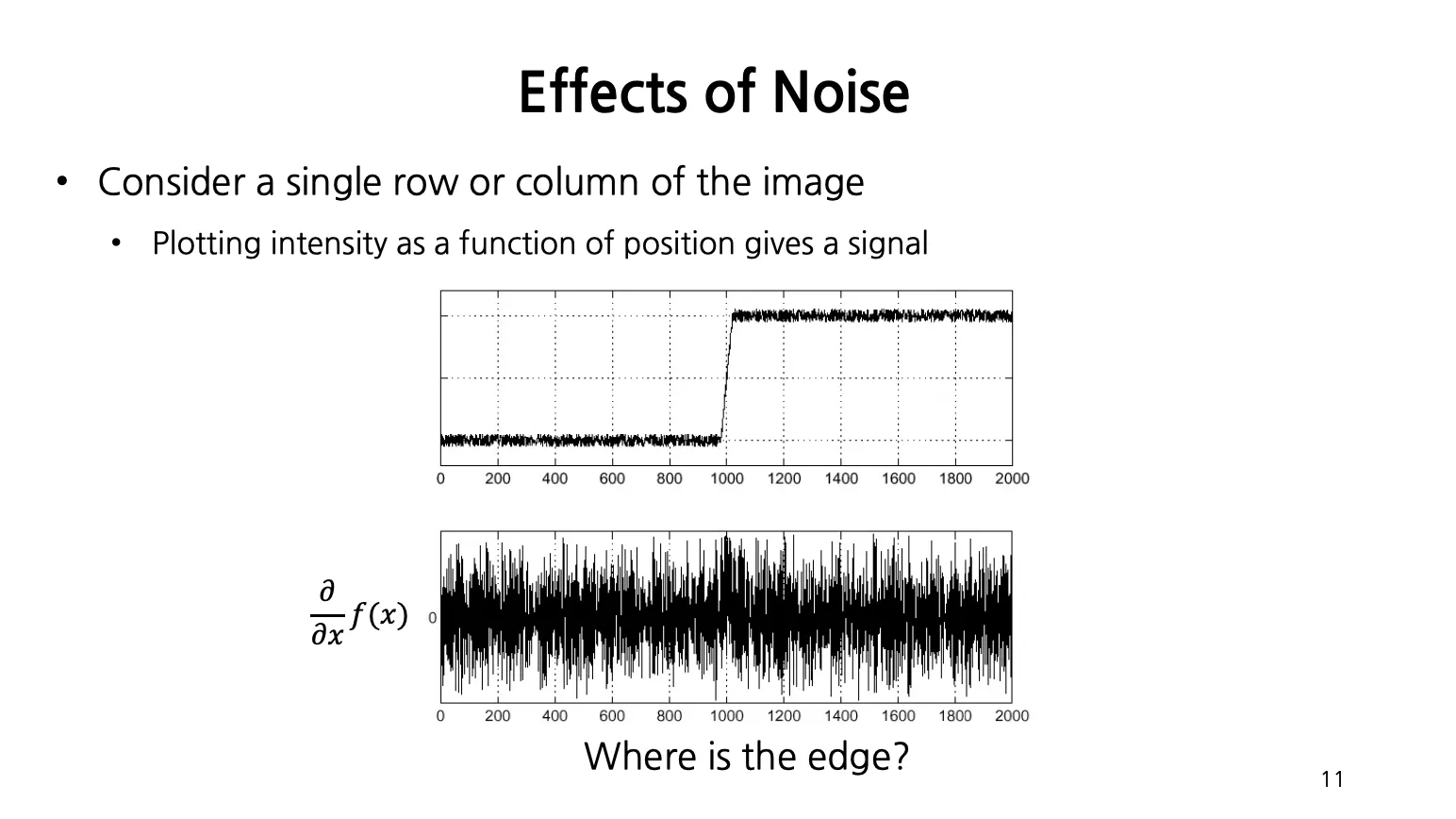
Effects of Noise

•
Signal 값이 급격히 변하는 1000 근처의 Edge 를 탐지하기를 원하지만, noise 때문에 gradient 값이 해당 부분 뿐만 아니라 전 구역에서 크기 때문에 제대로 Edge 를 탐지하기 어려움.
•
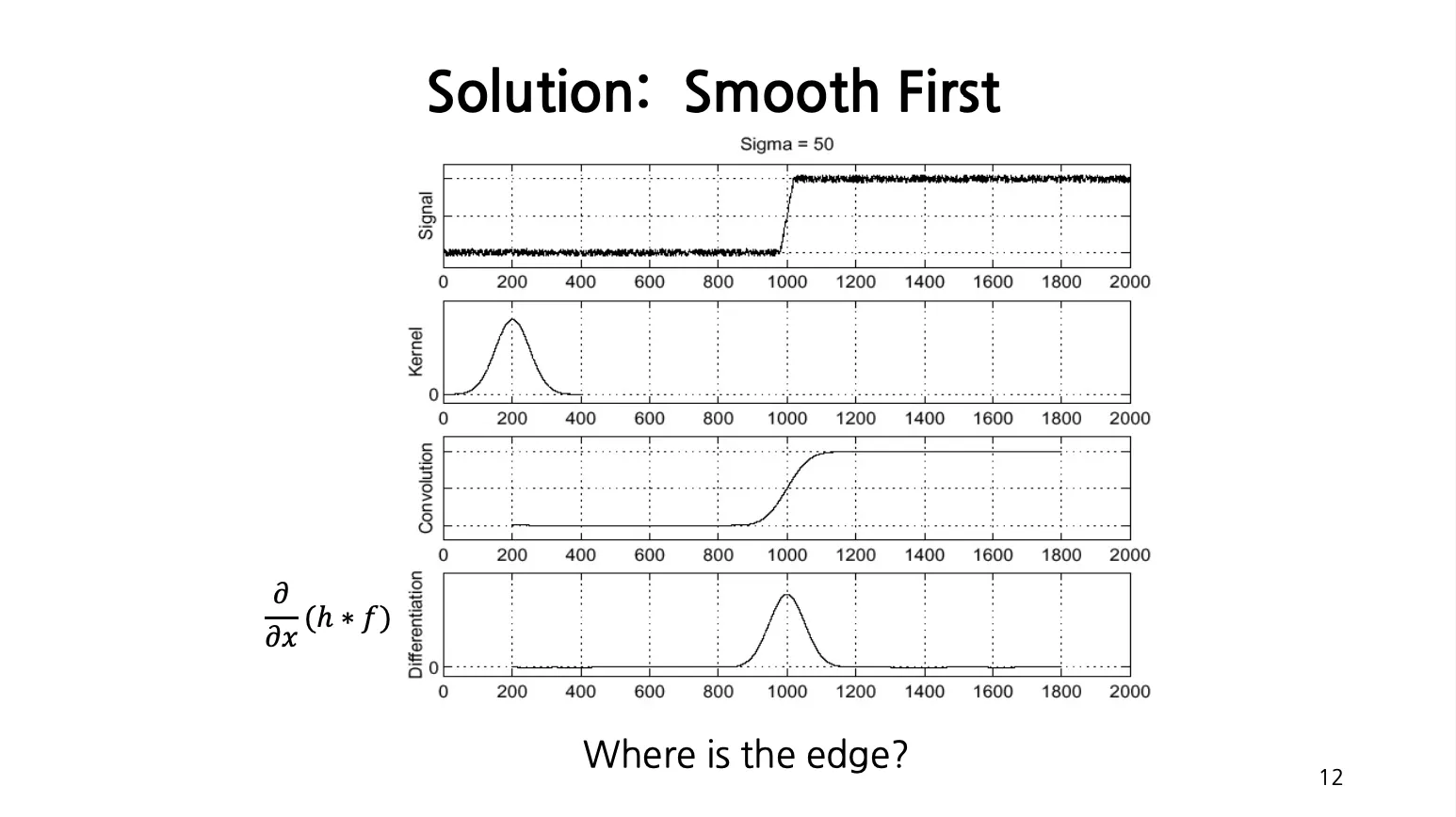
Solution: Smooth First
◦
Gaussian Filter 를 거쳐 smoothing 을 먼저하여 gradient 를 구함.
◦
∂∂x(h∗f)=(∂∂xh)∗f\frac{\partial}{\partial x}(h * f) = (\frac{\partial}{\partial x}h) * f 이므로 미리 미분된 gaussian 을 사용하면 전체 이미지에 대한 convolution 을 한 번만 해도 됨. (이미지 상에서 미분도 convolution operation 이므로…)
•
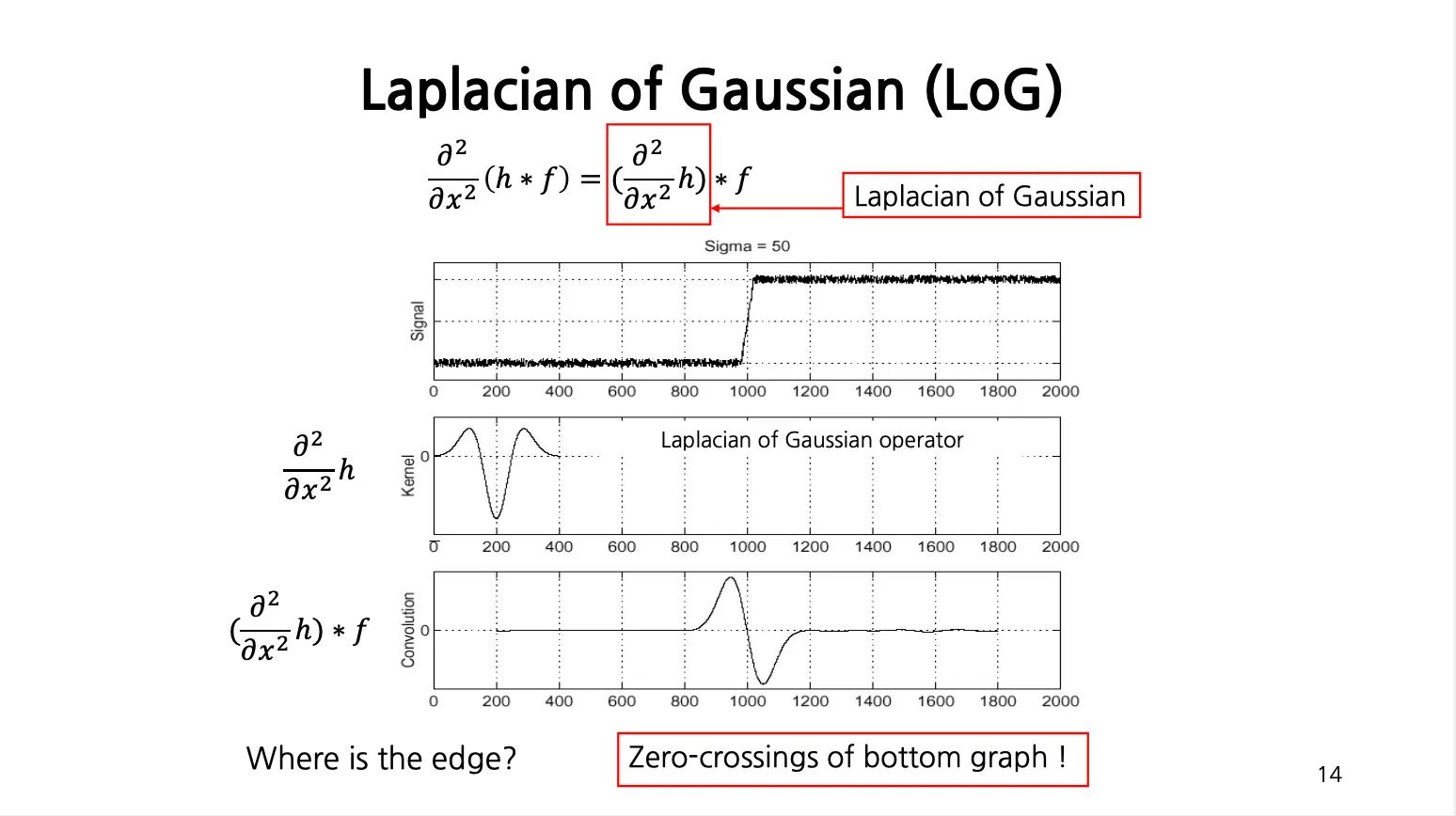
Laplacian of Gaussian (LoG) 을 사용하면 미분 값이 최대여서 Edge 가 탐지되었다고 볼 수 있는 지점들을 바로 검출해낼 수 있음. (2차 미분이 0 이 되는 지점들을 바로 찾을 수 있기 때문)
◦
2차 미분의 값도 0 이면서 양쪽의 부호가 바뀌는 부분을 Edge 로 볼 수 있음.

2D Gaussian Edge Operators

•
Gaussian 은 separable 하기 때문에 2D Gaussian 을 그대로 적용하진 않고 1D Gaussian 을 2번 적용하여 Computational Cost 의 이점을 챙길 수 있음. O(n2)→O(2n)O(n^2) \rarr O(2n)
•
Laplacian of Gaussian 은 Difference of Gaussian 으로 근사할 수 있음. 이를 이용하면 쉽게 Edge 부분을 얻어낼 수 있음.

Canny Edge Detector

1.
Input 을 먼저 grayscale 로 변환함.
2.
Gaussian Filter 를 이용해 input image 를 smoothing 함. (noise 가 있을 수 있기 때문)
a.
2D Gaussian 보다는 1D Gaussian 을 x, y 방향으로 1번씩!
3.
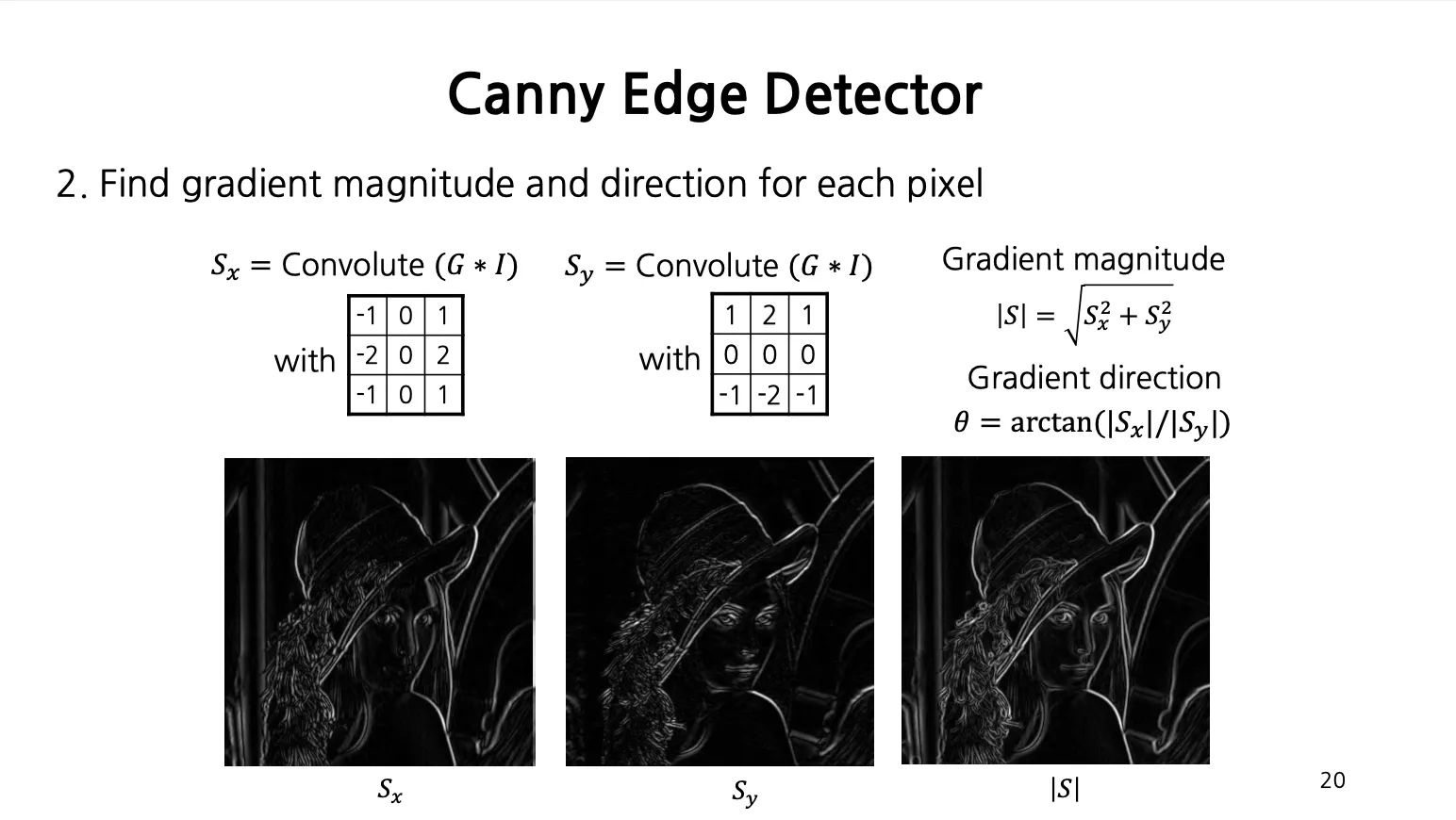
x 방향의 gradient kernel 과 y 방향의 gradient kernel 을 적용하면 SxS_x 와 SyS_y 가 얻어지고, 이들의 magnitude 를 구해서 gradient magnitude 에 대한 이미지인 ∣S∣|S| 를 얻을 수 있음
4.
Post-Processing 의 일환으로 Non-Maximum Suppresion 을 적용
a.
Maximum 이 아닌 값들은 조금 없애주겠다- 의 접근으로 Edge 를 sharp 하게 얻기 위한 과정임.
b.
Gradient 값이 정말 큰 부분이 아니면 이를 줄여서 Magnitude 가 작아지도록 하여 Edge 의 두께를 줄이는 과정임.
c.
특정 픽셀에서 gradient 의 방향과 크기를 알기 때문에 각 픽셀에서 그 만큼을 양과 음으로 이동해 보았을 때 나온 위치의 magnitude 를 interpolation 으로 구해낸 뒤에 해당 기준 픽셀이 양과 음으로 이동한 위치의 magnitude 보다 모두 높으면 max 값이라고 판단하여 살아남고 아니면 없앰.
E(x,y)={1,if ∥∇f(x,y)∥>T0, otherwiseE(x,y) = \begin{cases} 1, {\rm{if}}\ \| \nabla f(x,y) \| > T \\ 0, \ \rm otherwise\end{cases}
d.
Non-Maximum Suppresion 으로 Strong Edge 만을 남겼기 때문에 중간중간 끊어진 결과가 나올 수 있는데 이런 Weak Edge 가 실제로 Edge 이면 보정해주기 위해 주변의 Strong Edge 와의 connection 을 기반으로 두 개의 threshold 로 판단함.
∥∇f(x,y)∥≥T1→definitely an edge\| \nabla f(x,y) \| \ge T_1 \rarr \rm{definitely \ an \ edge}
T0≤∥∇f(x,y)∥<T1→maybe an edge, depends on contextT_0 \le \| \nabla f(x,y) \| < T_1 \rarr \rm{maybe\ an\ edge,\ depends\ on\ context}
T0>∥∇f(x,y)∥→definetly not an edgeT_0 > \| \nabla f(x,y)\| \rarr \rm{definetly\ not\ an\ edge}
만약 maybe an edge 에 속한다면 인접 픽셀이 strong edge 이면 edge 로 판별함. 이렇게 한다면 너무 끊기지는 않은 Edge Detection 결과를 얻을 수 있음.

Canny Edge Operator

•
요새는 Computer Vision Tool 에서 Canny Edge Detection 을 함수로 제공함.
•
하지만 Canny Edge Detection 의 첫 과정에 필요한 Gaussian Filtering 에서의 σ\sigma 에 따라 매우 다른 결과가 나오기 때문에 값을 조절할 필요가 있음.
◦
σ\sigma 를 작게 주면 빠르게 변하는 패턴도 detection 가능하지만 σ\sigma 를 크게 주면 이러한 패턴이 뭉개지기 때문에 detection 이 불가능함.
◦
반대로 σ\sigma 를 작게 주면 noise 도 detection 이 가능한 것이 단점임.
•
Parameter 세팅이 중요한데 σ\sigma 가 제일 중요하고 두 threshold 값도 중요함.