Duplicate

Lecture 9 | Photometric Stereo

수강 일자
2022/10/04

Image Intensity and 3D Geometry

•
2차원의 이미지를 보고도 대상 물체의 3차원 정보를 어느정도 예상할 수 있음.
◦
Shadow 정보에 의해서 3차원 정보를 유추할 수 있음.
◦
이미지 픽셀의 intensity 값으로부터 shape 을 유추할 수 있음. → Reflectance Map

Surface Normal

•
3차원 평면: Ax+By+Cz+D=0Ax+By+Cz+D = 0
◦
F(x,y,z)=f(x,y)−z=0F(x,y,z)=f(x,y)-z =0 으로도 표현할 수 있음.
◦
Surface Normal 은 −∇F(x,y,z)-\nabla F(x,y,z) 같이 표현할 수 있음.
▪
−∂z∂x=AC=p-\frac{\partial z}{\partial x} = \frac{A}{C}=p
▪
−∂z∂y=BC=q-\frac{\partial z}{\partial y} = \frac{B}{C}=q
▪
N=(AC,BC,1)=(p,q,1)N=(\frac{A}{C}, \frac{B}{C}, 1) = (p,q,1)

Gradient Space

•
Normal Vector
n=N∣N∣=(p,q,1)p2+q2+1n=\frac{N}{|N|}=\frac{(p,q,1)}{\sqrt{p^2+q^2+1}}
•
Source Vector (광원)
s=S∣S∣=(ps,qs,1)ps2+qs2+1s=\frac{S}{|S|}=\frac{(p_s,q_s,1)}{\sqrt{p_s^2+q_s^2+1}}
•
z=1z=1 평면은 Gradient Space 라고 불림.
◦
어떤 orientation 이 주어지던간에 Gradient Space 의 point 로 mapping 이 가능함.
cos⁡θi=n⋅s=pps+qqs+1p2+q2+1ps2+qs2+1\cos\theta_i=n\cdot s=\frac{pp_s+qq_s+1}{\sqrt{p^2+q^2+1}\sqrt{p_s^2+q_s^2+1}}
◦
θi\theta_i 는 source vector 와 normal vector 사이의 각도

Reflectance Map

•
Image Intensity I(x,y)I(x,y) 를 surface orientation (p,q)(p,q) 와 관계짓는 것.
•
Lambertian Case (Diffusion Reflection 만 고려)
◦
kk: source brightness (II)
◦
ρ\rho: surface albedo
◦
cc: normalization constant
◦
Image Intensity
I=ρπkccos⁡θi=ρπkc n⋅sI=\frac{\rho}{\pi}kc\cos\theta_i= \frac{\rho}{\pi}kc\ n\cdot s
▪
특점 점에서의 Radiance 와 Image Intensity 는 cc 라는 비례상수를 가지는 비례관계 (L=ρπkcos⁡θi)L=\frac{\rho}{\pi}k\cos\theta_i)
▪
ρπkc=1\frac{\rho}{\pi}kc=1 로 두면, I=cos⁡θi=n⋅sI=\cos\theta_i=n\cdot s 가 됨.
▪
Reflection Map R(p,q)R(p,q) 는 다음과 같이 표현됨.
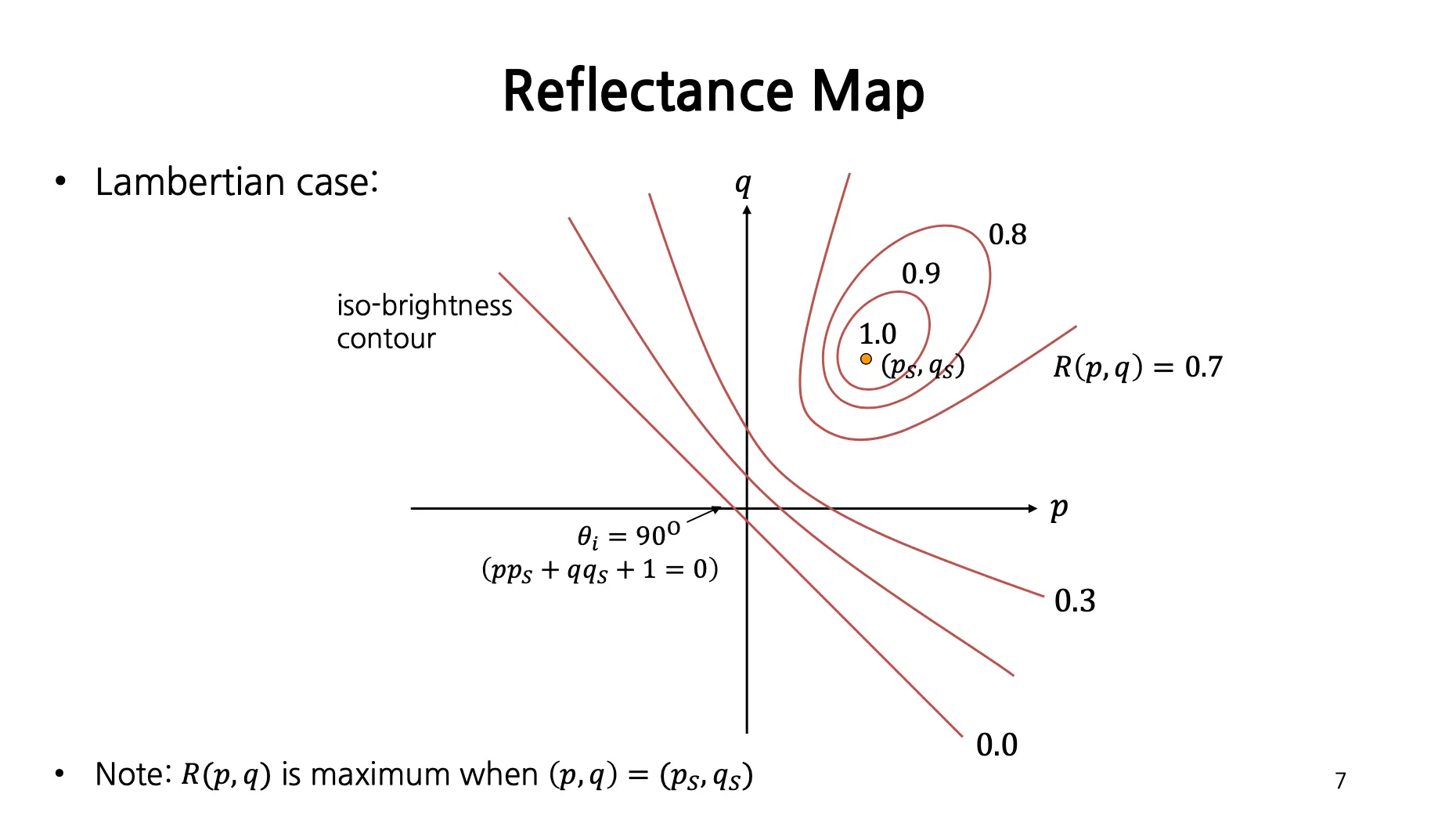
I=cos⁡θi=n⋅s=pps+qqs+1p2+q2+1ps2+qs2+1=R(p,q)I=\cos\theta_i = n\cdot s= \frac{pp_s+qq_s+1}{\sqrt{p^2+q^2+1}\sqrt{p_s^2+q_s^2+1}}=R(p,q)
•
Source Vector 와 동일한 각도를 이루는 normal vector 들을 가지는 Surface (Cone 영역의 normal vector 들) 에 대해서는 동일한 Image Intensity 를 가짐. 이러한 normal vector 들은 Gradient Space 로 mapping 하게 되면 타원형태가 됨. → Iso-brightness contour 라고 함.
◦
Gradient Space 상의 Iso-brightness contour 는 아래와 같음.
▪
각도가 0°0\degree 일 때 값은 1.0 이 되며 점 형태로 그려지고, 각도가 커질수록 값이 작아지며 타원이 커지는 것을 볼 수 있음.

Shape from a Single Image?

•
Source Direction (ps,qs)(p_s,q_s), Sufrace Reflection ρ\rho, Image Intensity I(x,y)I(x,y) 를 알고 있다고 하더라도, surface orientation (p,q)(p,q) 를 unique 하게 결정할 수는 없음. (contour 상에 존재하는 여러 점들이 후보가 됨.)
•
즉, 한 장의 이미지만 얻어서는 unique 하게 Surface Normal 을 얻어낼 수 없음.
◦
첫 번째 option 은 사진을 여러 장 찍는 방법임. → Photometric Stereo
▪
물체 및 카메라는 고정한 채로, 광원을 돌려가면서 변화하는 Image Intensity 를 얻어냄.
◦
두 번째 option 은 constraint 를 주어 후보 중 하나를 선택하는 방법임. → Shape-from-Shading (그림자로부터 3D Shape 을 예측하는 방법으로, 강의에서 다루지는 않음.)

Photometric Stereo

•
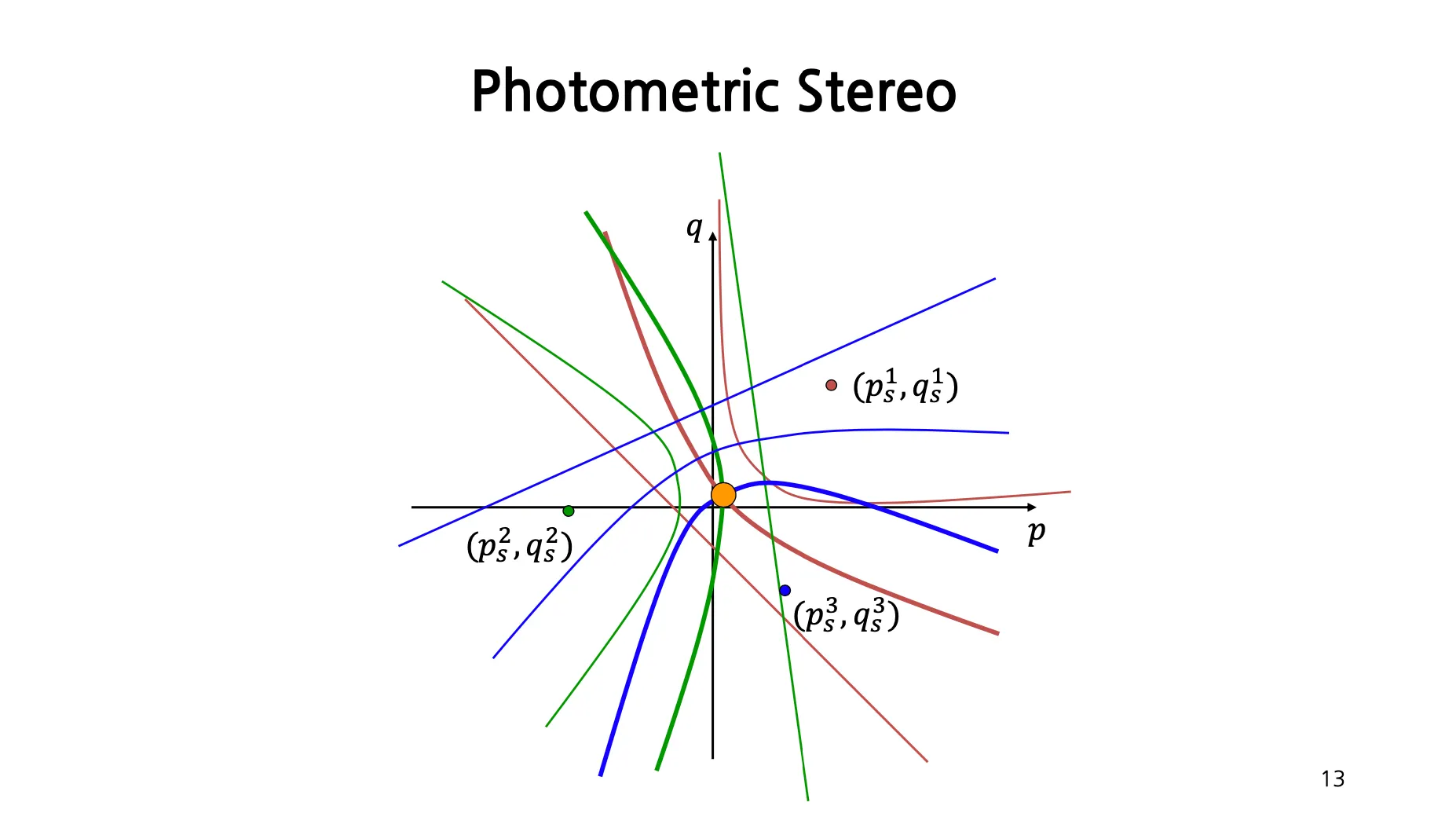
광원 (ps1,qs1)(p_s^1,q_s^1), (ps2,qs2)(p_s^2,q_s^2), (ps3,qs3)(p_s^3, q_s^3) 에 대해서 Image Intensity 를 추출하고 특정 픽셀이 가질 수 있는 Surface Normal 에 대한 iso-brightness contour 를 그릴 수 있음.
•
Iso-brightness contour 의 교점에 해당하는 (p,q)(p,q) 가 실제 물체의 Surface Normal 값임.
•
I=ρπkccos⁡θi=ρ n⋅s (kcπ=1)I=\frac{\rho}{\pi}kc\cos\theta_i=\rho\ n\cdot s\ (\frac{kc}{\pi}=1)
◦
[I1I2I3]=[s1Ts2Ts3T]ρn\begin{bmatrix} I_1 \\ I_2 \\ I_3 \end{bmatrix} = \begin{bmatrix} s_1^T \\ s_2^T \\ s_3^T \end{bmatrix} \rho n
◦
n~=S−1I\tilde n= S^{-1}I
◦
ρ=∣n~∣\rho = |\tilde n|
◦
n=n~∣n~∣=n~ρn = \frac{\tilde n}{|\tilde n|}=\frac{\tilde n}{\rho}

More then Three Light Sources

•
Source Direction 의 측정 오차나 가정등으로 인해서 일반적으로 세 번보다는 많은 광원 위치변경을 사용함.
[I1⋮IN]=[s1T⋮sNT]ρn\begin{bmatrix} I_1 \\ \vdots \\ I_N \end{bmatrix} = \begin{bmatrix} s_1^T \\ \vdots \\ s_N^T \end{bmatrix} \rho n
◦
Ideal 하게는 같아야 하지만, 오차에 의해서 그럴 수 없을 수 있으니 좌변과 우변의 차이를 최소화하는 방법을 사용. (Least Square Solution)
◦
I=Sn~I=S\tilde n
◦
STI=STSn~S^TI=S^TS\tilde n
◦
n~=(STS)−1STI\tilde n=(S^TS)^{-1}S^TI → Moore-Penrose pseudo inverse

Color Images

•
각 color channel 마다의 equation 을 얻어낼 수 있음.
IR=ρRSnIG=ρGSnIB=ρBSnI_R = \rho_R Sn\\ I_G = \rho_G Sn\\ I_B = \rho_B Sn\\
◦
하나의 equation 만 집중하여 nn 을 얻어낸 뒤에 ρ\rho 값들을 대입하여 얻어낼 수 있음.
◦
또는, 세 channel 의 intensity 를 합쳐서 최종적으로 하나의 nn 을 구해낼 수도 있음.
I=IR2+IG2+IB2=ρSnI=\sqrt{I_R^2 + I_G^2 + I_B^2} = \rho S n

Computing Light Source Directions

•
앞서 Surface Normal 을 구하는 Photometric Stereo 방법론은 Light Source 의 direction 이 주어져야 진행할 수 있었음.
•
직접 Light Source 를 컨트롤할 수 있다면 문제가 없지만 그렇지 못한 경우에 접근할 수 있는 방법론을 생각해볼 필요가 있음.

Specular Reflection - Recap

•
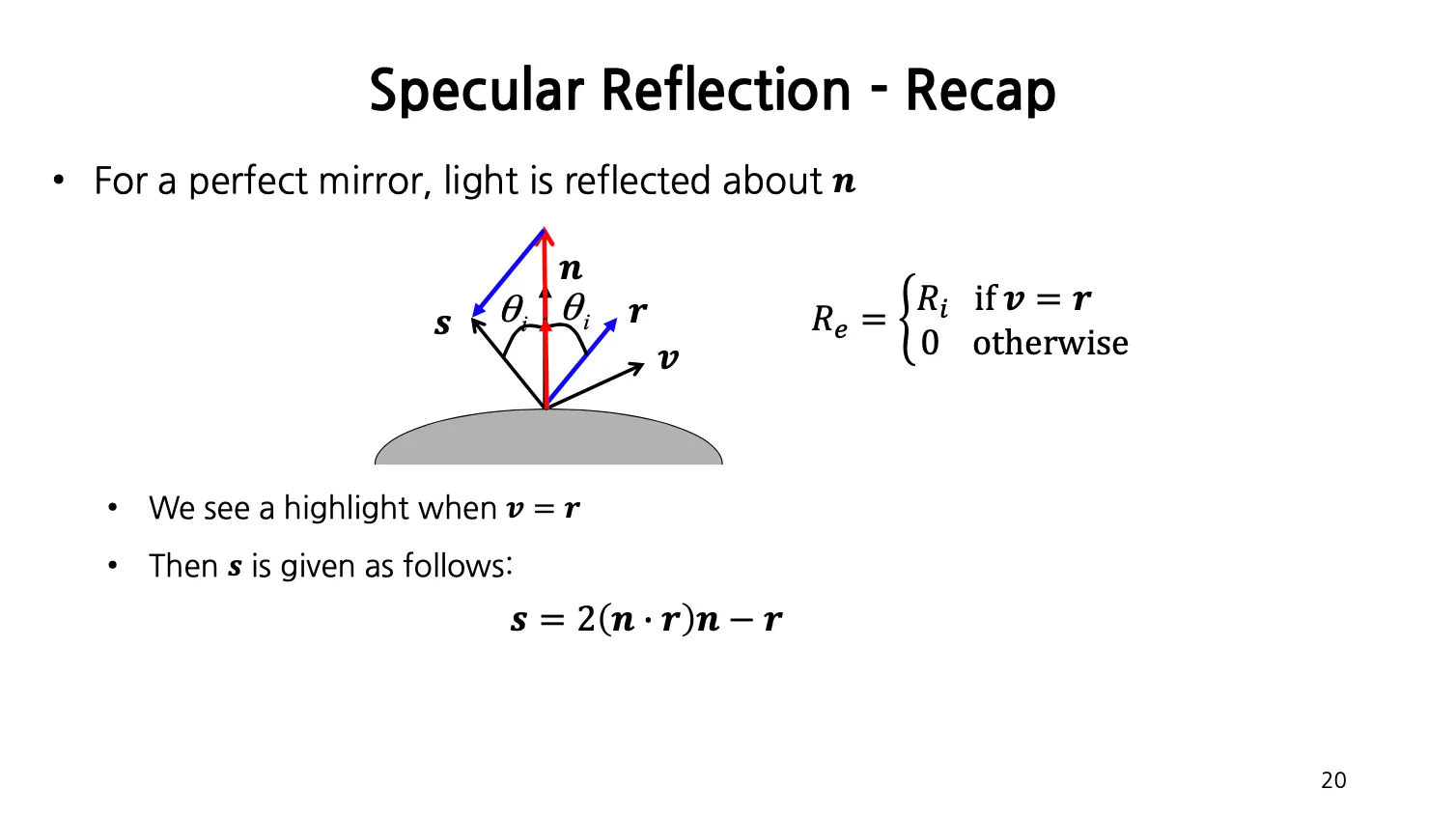
정확히 반대 방향으로 모든 빛이 반사되는 경우가 Specular Reflection.
•
구체의 highlighted 된 위치는 view direction 과 반사되어 나가는 빛의 direction 이 같아질 때 (v=rv=r) 나타남.
s=2(n⋅r)n−rs=2(n\cdot r)n-r
◦
nn 과 rr 을 알고 있으면 source direction ss 를 구할 수 있음.
•
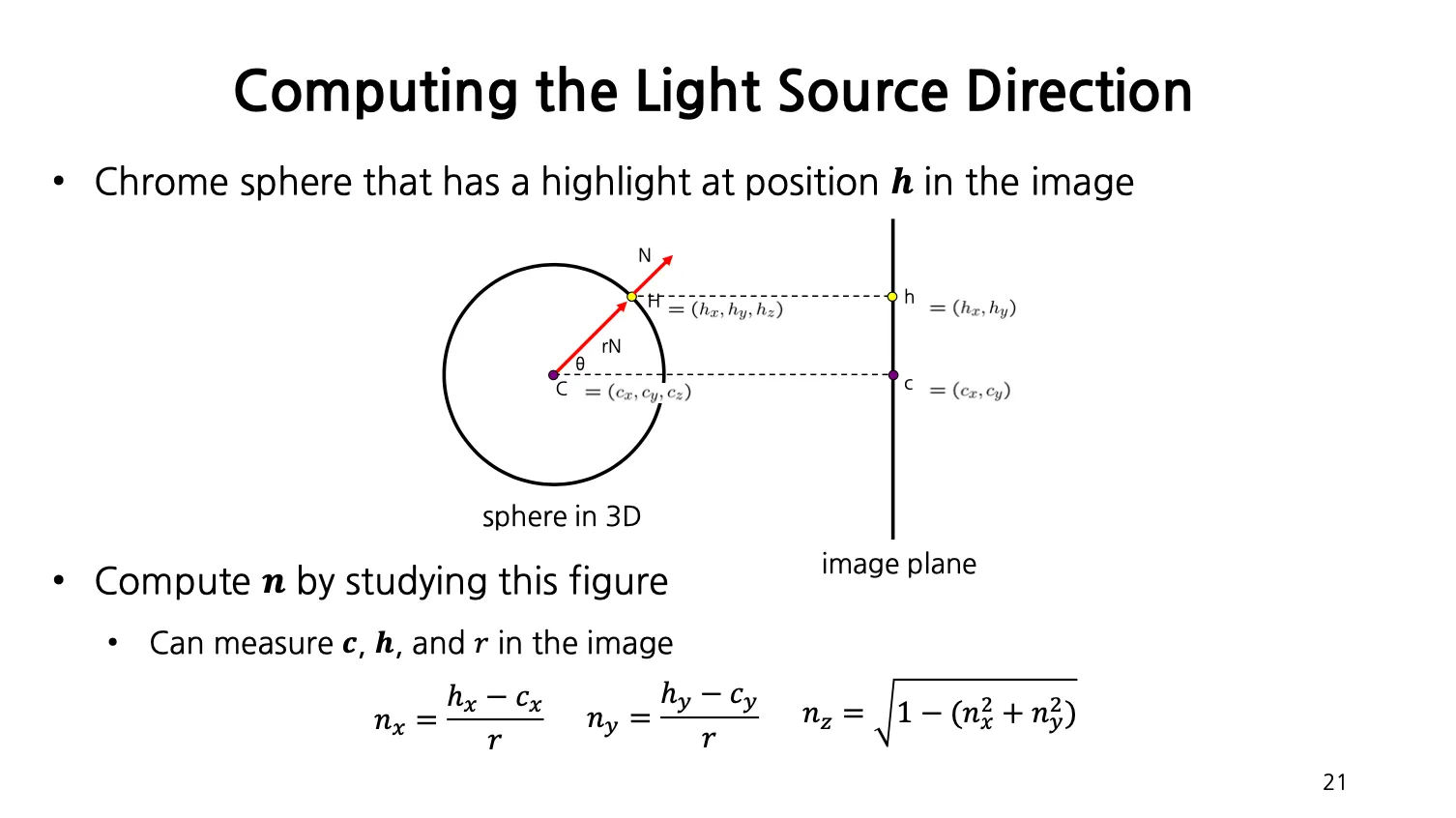
rr 은 카메라의 방향과 같을 때 highlighted region 을 생각하는 것이므로 구할 수 있음.
•
nn 의 경우에는 아래와 같이 구할 수 있음.
◦
hxh_x, hyh_y 는 이미지 상에서 highlighted 된 부분의 좌표
◦
cxc_x, cyc_y 는 이미지 상에서 구체의 중심 좌표
◦
rr 은 구체의 반지름
◦
nx=hx−cxrn_x = \frac{h_x-c_x}{r}, ny=hy−cyrn_y=\frac{h_y-c_y}{r}, nz=1−(nx2+ny2)n_z=\sqrt{1-(n_x^2+n_y^2)}

Limitations

•
Big Problems
◦
Lambertian Surface 는 이상적인 Surface 이기 때문에 반짝이거나 반투명하면 잘 동작하지 않음.
◦
Shadow 에 해당하는 부분은 Surface Normal 을 알아내기 어려움.
◦
완전이 control 된 방이면 좋은데 inter-reflection 이 심한 곳 같으면 동작하기 어려움.
•
Smaller Problems
◦
카메라와 광원이 충분한 거리를 두고 떨어져 있어야 함.
◦
Calibration 이 필요함.
▪
Light source direction 과 intensity 를 측정해야 함. (더군다나 light source intensity 가 2배가 된다해서 측정 intensity 가 2배가 되지는 않음.)
▪
LL 과 II 에 대한 관계가 실제로는 non linear 하는 등 복잡한 관계를 고려하지 않음.

Trick for Handling Shadows

•
Ii(Ii)=Ii(ρn⋅si)I_i(I_i)=I_i(\rho n\cdot s_i) 와 같이 양 변에 pixel brightness 를 곱해주면 shadow 에 대한 보정 (영향을 줄일 수 있다) 이 가능하다는 것이 실험적으로 밝혀짐.
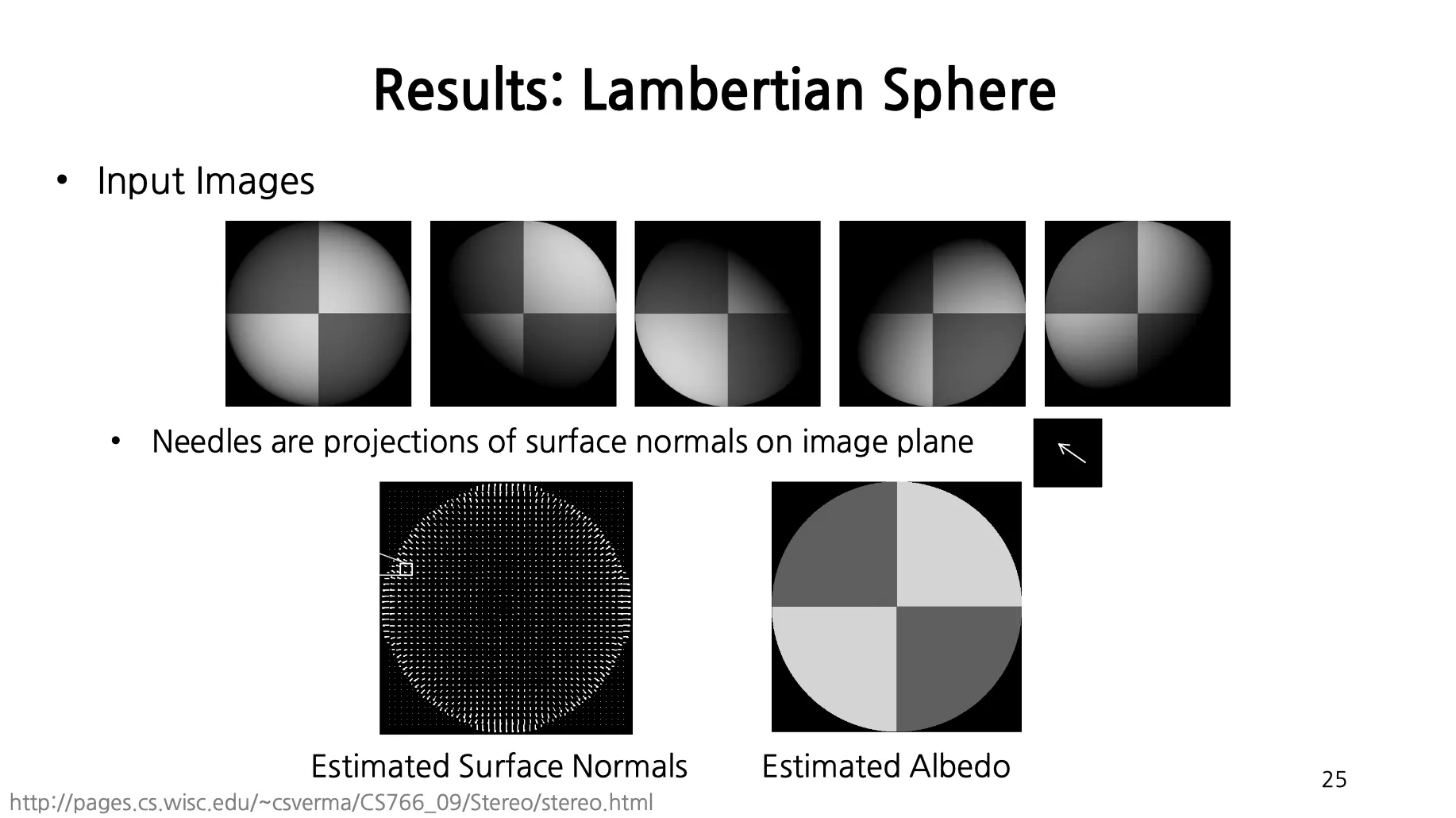
[I12⋮IN2]=[I1s1T⋮INsNT]ρn\begin{bmatrix} I_1^2 \\ \vdots \\ I_N^2 \end{bmatrix} = \begin{bmatrix} I_1s_1^T \\ \vdots \\ I_Ns_N^T \end{bmatrix} \rho n

Results: Lambertian Sphere

•
광원을 돌려가며 5장의 사진을 찍으면, 모든 점에 대해서 Surface Normal 과 Albedo 를 측정할 수 있음.