Duplicate

Lecture 5 | Homography Estimation

수강 일자
2023/02/24

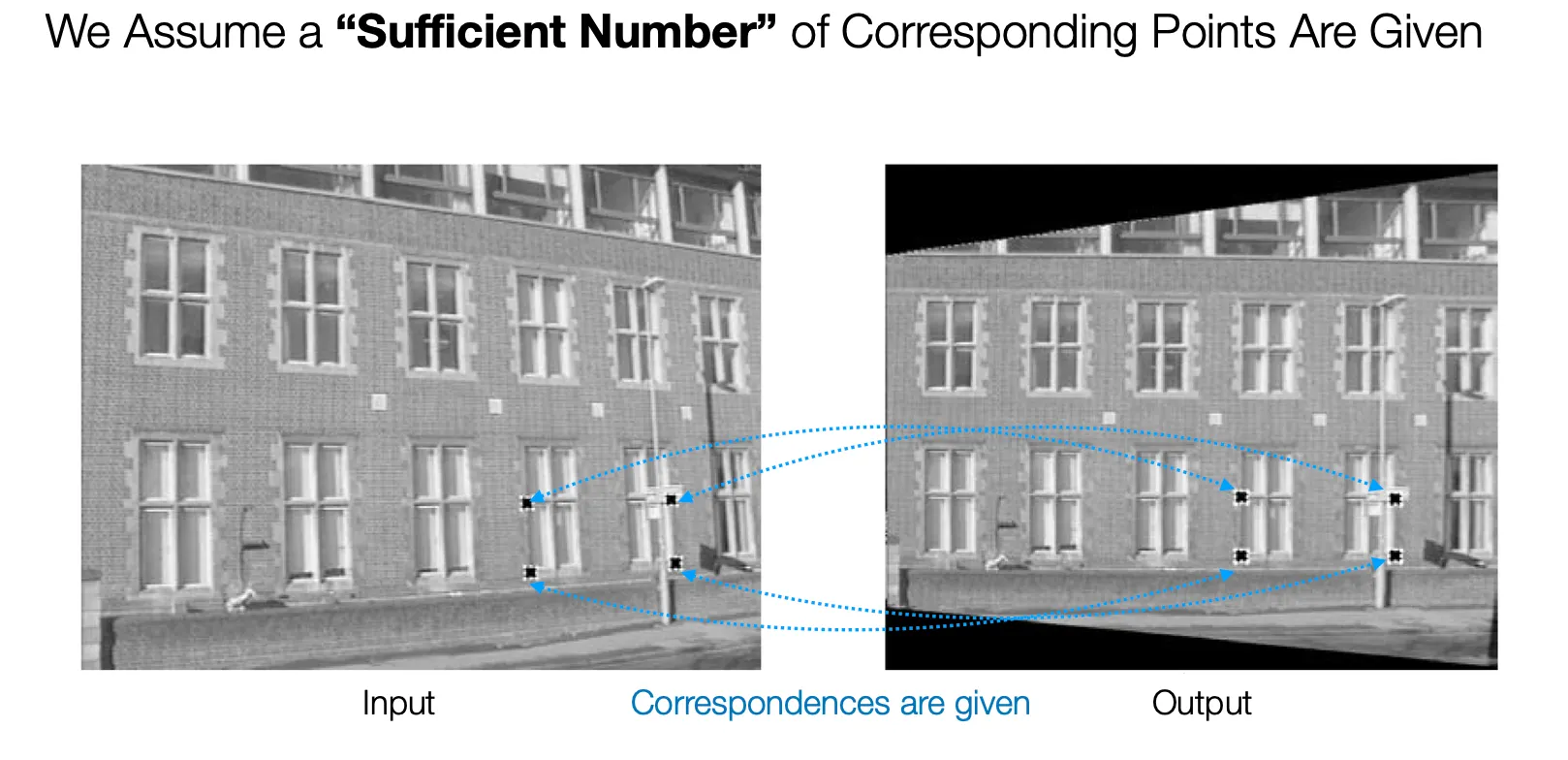
Removing Perspective Distortion

•
두 이미지 간의 Homography 를 찾기 위해서는 Corresponding Points 들이 필요함.

Direct Linear Transform (DLT)

[xi′yi′1]=[h11h12h13h21h22h23h31h32h33]=[xiyi1]\begin{bmatrix} x_i' \\ y_i' \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} = \begin{bmatrix} x_i \\ y_i \\ 1 \end{bmatrix}
•
위 식을 일반적인 Homography 변환에 대한 대응 식임.
•
이를 다음과 같이 x′,y′x', y' 에 대해 나타낼 수 있음.
x′=h11x+h12y+h13h31x+h32y+h33y′=h21x+h22y+h23h31x+h32y+h33x' = \frac{h_{11}x + h_{12}y +{h_{13}}}{h_{31}x + h_{32}y + h_{33}} \quad y' = \frac{h_{21}x + h_{22}y +{h_{23}}}{h_{31}x + h_{32}y + h_{33}}
•
위 식을 풀어서 H{\rm H} 의 각 항목에 대한 식으로 변환하면 다음과 같음.
[xy1−x′x−x′y−x′xy1−y′x−y′y−y′][h11h12h13h21h22h23h31h32h33]=02×1\begin{bmatrix} x & y & 1 & & & & -x'x & -x'y & -x' \\ & & & x & y & 1 & -y'x & -y'y & -y' \end{bmatrix} \begin{bmatrix} h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \\ \end{bmatrix} = 0_{2\times 1}
•
4 개의 Corresponding Points 들이 있다면 다음과 같이 식을 구성할 수 있음.
[x1y11−x1′x1−x1′y1−x1′x1y11−y1′x−y1′y1−y1′x2y21−x2′x2−x2′y2−x2′x2y21−y2′x2−y2′y2−y2′x3y31−x3′x3−x3′y3−x3′x3y31−y3′x3−y3′y3−y3′x4y41−x4′x4−x4′y4−x4′x4y41−y4′x4−y4′y4−y4′][h11h12h13h21h22h23h31h32h33]=02×1\begin{bmatrix} x_1 & y_1 & 1 & & & & -x_1'x_1 & -x_1'y_1 & -x_1' \\ & & & x_1 & y_1 & 1 & -y_1'x & -y_1'y_1 & -y_1' \\ x_2 & y_2 & 1 & & & & -x_2'x_2 & -x_2'y_2 & -x_2' \\ & & & x_2 & y_2 & 1 & -y_2'x_2 & -y_2'y_2 & -y_2' \\ x_3 & y_3 & 1 & & & & -x_3'x_3 & -x_3'y_3 & -x_3' \\ & & & x_3 & y_3 & 1 & -y_3'x_3 & -y_3'y_3 & -y_3' \\ x_4 & y_4 & 1 & & & & -x_4'x_4 & -x_4'y_4 & -x_4' \\ & & & x_4 & y_4 & 1 & -y_4'x_4 & -y_4'y_4 & -y_4' \end{bmatrix} \begin{bmatrix} h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \\ \end{bmatrix} = 0_{2\times 1}
◦
8DoF 이기 때문에 4 개의 Corresponding Points 로도 식의 해를 구할 수 있음.
▪
다만, 많은 Corresponding Points 로도 구할 수 있고, 이는 Corresponding Points 의 측정에 오류가 있는 경우에 정확해짐.
◦
SVD 를 사용하여 ∥h∥=1\|h\| = 1 에서 ∥Ah∥\|Ah\| 를 최소화하는 문제를 풀면 다음 식의 해를 구할 수 있음.
∥Ah∥=(Ah)T(Ah)=hTATAh=hT(VDTUT)(UDVT)h=hTVDTDVTh=(VTh)T(D2)(VTh)=σ12x12+…σn2xn2where x=VTh→∥x∥2=1≥σi2xarg min⁡iσi2\begin{align*} \|Ah\| &= (Ah)^T(Ah) \\ &= h^TA^TAh& \\ &= h^T(VD^TU^T)(UDV^T)h \\ &= h^TVD^TDV^Th \\ & = (V^Th)^T(D^2)(V^Th) \\ & = \sigma_1^2x_1^2 + \dots \sigma_n^2x_n^2 \quad {\rm where}\ x=V^Th \to \| x\|^2 = 1 \\ & \ge \sigma_i^2x_{\argmin_i \sigma_i}^2 \end{align*}
▪
xx 가 arg min⁡iσi\argmin_i \sigma_i 인 index 만 1 이고 나머지는 0 일 때 식이 최솟값을 가지며, 이러기 위한 hh 는 가장 작은 eigenvalue 와 대응되는 eigenvector 임.
•
직접적으로 multiplication form 을 만들지 않더라도 Cross Product 를 통해 Up-to-Scale 문제를 해결할 수 있음.
xi′×Hxi′=0{\rm x_i'} \times {\rm H}{\rm x_i'} = 0

What if We Only Want to Remove Some Properties?

•
두 개의 이미지 사이의 변환이 아니라, Projective Transform 된 이미지에서 Affine Transform 요소만 남기고 싶은 경우에는 2DoF 만을 줄여야 함.

Affine Rectification

•
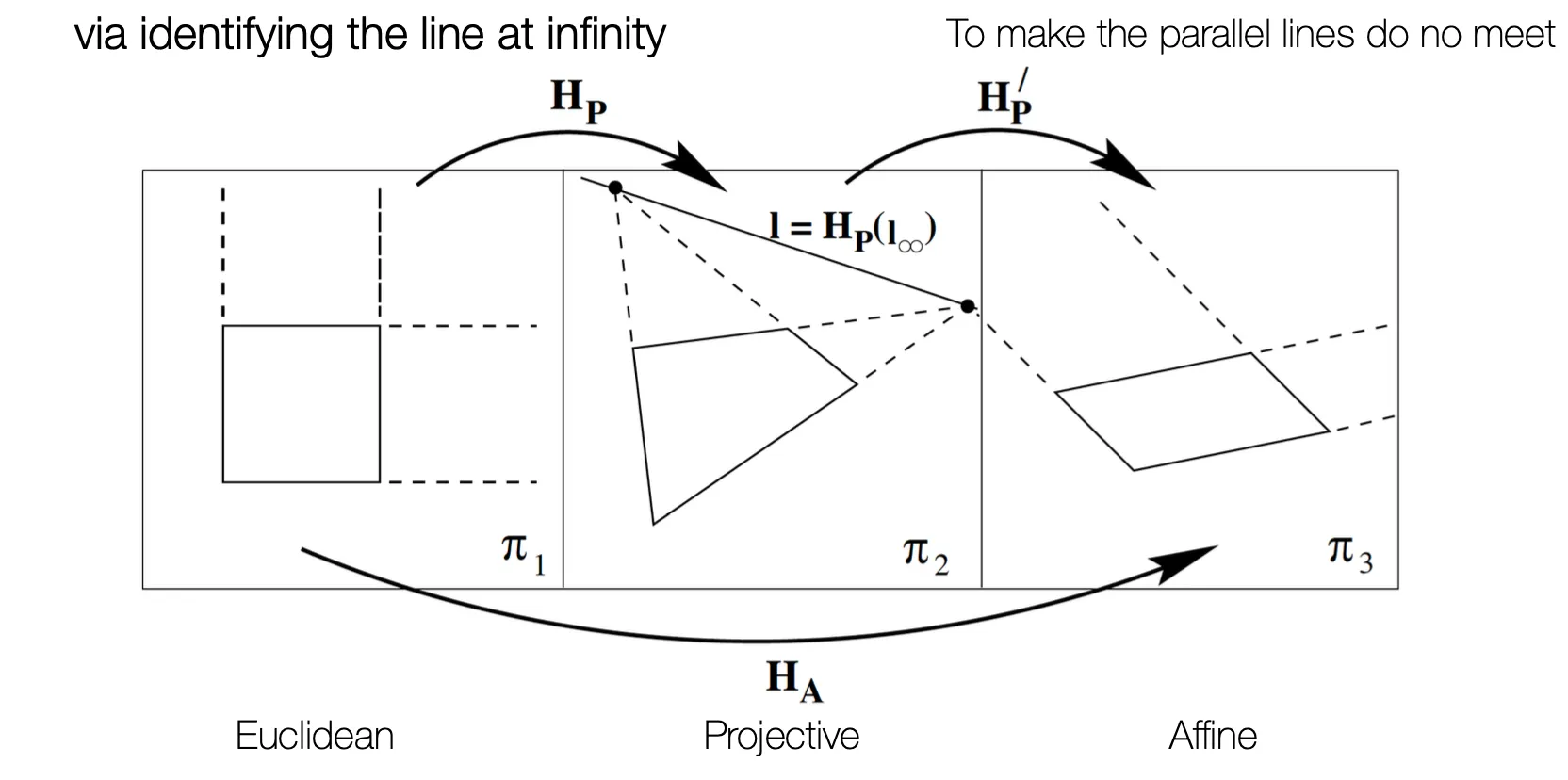
Affine Rectification 은 Projective Transform 이미지에서 Affine 요소만 남기는 변환임.
•
Euclidean 이 Projective Transform 이 되면, 평행한 선이 한 점에서 만나게 됨.
◦
평행한 선들의 교점이 만드는 선인 Line at Infinity 가 Hp(l∞){\rm H_p}(\rm l_{\infty})
•
Affine 의 특성은 parallelism 이기 때문에 Line at Infinity 를 다시 Infinity (0,0,1)T(0, 0,1)^T 로 보내는 변환을 통해 Projective Transform 으로 변환된 이미지에서 Affine 요소만 남길 수 있음.

Affine Rectification

•
Projective Transform 이미지에서 Line at Infinity 는 평행한 선의 교점을 두 쌍 구하고, 두 개의 교점을 지나는 선을 구하는 방법으로 구해낼 수 있음.
•
Line at Infinity 를 다시 (0,0,1)T(0,0,1)^T 로 보내기 위해 다음과 같은 식을 고려할 수 있음.
l′=H−Tll′∞=[l1l2l3]=H−T[001]{\rm l'} = {\rm H}^{-T}{\rm l} \\ {\rm l'}_{\infty} = \begin{bmatrix} l_1 \\ l_2 \\ l_3 \end{bmatrix} = {\rm H}^{-T} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}
◦
H{\rm H} 는 Affine 에서 Projective Transform 으로 가는 point 에 대한 Homography Matirx 임.
•
위 식의 H\rm H 단순하게 다음과 같이 구해낼 수 있음.
HT[l1l2l3]=[001]HT=[10−l1l301−l2l3001l3]{\rm H}^T \begin{bmatrix} l_1 \\ l_2 \\ l_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \\ \quad \\ {\rm H}^T = \begin{bmatrix} 1 & 0 & -\frac{l_1}{l_3} \\ 0 & 1 & -\frac{l_2}{l_3} \\ 0 & 0 & \frac{1}{l_3} \end{bmatrix}
◦
여기서 구해낸 H{\rm H} 에 다른 어떠한 Affine Transform HA{\rm H}_A 를 사용해 Left Multiplication 을 해도 Affine Transform 은 Line at Infinity 를 변경하진 못하기 때문에 이 또한 해가 될 수 있음.
HT=HAT[10−l1l301−l2l3001l3]→HT[l1l2l3]=[001]{\rm H}^T = {\rm H}^T_A \begin{bmatrix} 1 & 0 & -\frac{l_1}{l_3} \\ 0 & 1 & -\frac{l_2}{l_3} \\ 0 & 0 & \frac{1}{l_3} \end{bmatrix} \to {\rm H}^T \begin{bmatrix} l_1 \\ l_2 \\ l_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}

Metric Rectification

•
Affine Rectification 때와 마찬가지로 Affine Transform 된 이미지에서 Similarity Transformation 으로 변경하려고 할 경우를 고려해 볼 수 있음.

Circular Points are Fixed Under Similarity Transformations

•
Circular Points 는 다음과 같은 점들임.
I=(1i0)J=(1−i0){\rm I} = \begin{pmatrix} 1 \\ i \\ 0 \end{pmatrix} \quad {\rm J} = \begin{pmatrix} 1 \\ -i \\ 0 \end{pmatrix}
•
놀라운 점은, Circular Points 에 Similarity Transform 을 거쳐도 본인이 나옴.
I′=HsimilarityI=[scos⁡θ−ssin⁡θtxssin⁡θscos⁡θtx001](1i0)=se−iθ(1i0)=I\begin{align*} {\rm I}' &= {\rm H}_{\rm similarity} {\rm I} \\ &= \begin{bmatrix} s\cos\theta & -s\sin\theta & t_x\\ s\sin\theta & s\cos\theta & t_x\\ 0 & 0 & 1 \end{bmatrix} \begin{pmatrix} 1 \\ i \\ 0 \end{pmatrix} \\ &= se^{-i\theta} \begin{pmatrix} 1 \\ i \\ 0 \end{pmatrix} = {\rm I} \end{align*}
•
더 놀라운 점은, 이러한 Circular Points 가 마냥 의미없는 점들은 아니라는 것임.
◦
모든 원들과 Line at Infinity 의 유일한 교점이 I,J{\rm I, J} 임…

The Conic Dual to The Circular Points

C∞∗=IJT+JITC∞∗=(1i0)(1−i0)+(1−i0)(1i0)=[100010000]C^*_{\infty} = {\rm I}{\rm J}^T + {\rm J}{\rm I}^T \\ \quad \\ C^*_{\infty} = \begin{pmatrix} 1 \\ i \\ 0 \end{pmatrix} \begin{pmatrix} 1 & -i & 0 \end{pmatrix} + \begin{pmatrix} 1 \\ -i \\ 0 \end{pmatrix} \begin{pmatrix} 1 & i & 0 \end{pmatrix} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}
•
정성적으로는, I,J{\rm I}, {\rm J} 를 지나는 직선 모두에 수직인 conic 을 나타냄.
•
이 Conic 은 마찬가지로 특이하게도 Similarity Transform 에 invariant 함.
◦
일반적인 Projective Transform 은 Similarity + Affine + Projective 의 곱으로 나타낼 수 있음.
H=HSHAHP=[sRt0T1][K00T1][I0vTv]{\rm H} = {\rm H}_S{\rm H}_A{\rm H}_P = \begin{bmatrix} s{\rm R} & {\rm t} \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} {\rm K} & 0 \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} {\rm I} & 0 \\ {\rm v}^T & v \end{bmatrix}
◦
이 특성을 활용하면 일반적인 Projective Transform 에서 conic 이 다음과 같이 변함.
C∗∞′=(HPHAHS)C∞∗(HPHAHS)T=(HPHA)(HSC∞∗HST)(HAHP)=(HPHA)C∞∗(HAHP)=[KKTKKTvvTKKTvTKKTv]\begin{align*} {\rm C^*}_{\infty}' &= ({\rm H}_P{\rm H}_A{\rm H}_S)C^*_{\infty}({\rm H}_P{\rm H}_A{\rm H}_S)^T = ({\rm H}_P{\rm H}_A)({\rm H}_SC^*_{\infty}{\rm H}_S^T)({\rm H}_A{\rm H}_P) \\ & = ({\rm H}_P{\rm H}_A)C^*_{\infty}({\rm H}_A{\rm H}_P)\\ &= \begin{bmatrix} {\rm K}{\rm K}^T & {\rm K}{\rm K}^T{\rm v} \\ {\rm v}^T{\rm K}{\rm K}^T & {\rm v}^T{\rm K}{\rm K}^T{\rm v} \end{bmatrix} \end{align*}

Why Do We Care the Dual Conic?

•
Dual Conic 을 다룬 이유는 이 친구의 invariance 가 Similairty Transform 에서의 angle 의 invariance 를 보이는데 쓰일 수 있기 때문임.
•
일반적으로 선 l=(l1,l2,l3){\rm l} = (l_1, l_2, l_3) 과 m=(m1,m2,m3){\rm m} =(m_1, m_2, m_3) 의 cosine 각도는 다음과 같음.
cos⁡θ=l1m1+l2m2(l12+l22)(m12+m22)\cos\theta = \frac{l_1m_1 +l_2m_2}{\sqrt{(l_1^2 + l_2^2)(m_1^2 + m_2^2)}}
•
위 식은 Circular Points 에 Dual 한 Conic 을 활용하여 다음과 같이 표현할 수 있음.
cos⁡θ=lTC∞∗m(lTC∞∗l)(mTC∞∗m)\cos\theta = \frac{{\rm l}^TC^*_{\infty}{\rm m}}{\sqrt{(\rm l^TC^*_{\infty}{\rm l})({\rm m}^TC^*_{\infty}{\rm m})}}
◦
놀라운 점은 위의 모든 선에 대해 다음 형태가 Similarity Transform invariant 하다는 것임…
lTC∞∗m→(H−Tl)T(HC∞∗HT)(H−Tm)=lTC∞∗m{\rm l}^TC^*_{\infty}{\rm m} \to ({\rm H}^{-T}{\rm l})^T (H C^*_{\infty}H^T)(H^{-T}{\rm m}) = {\rm l}^TC^*_{\infty}{\rm m}
▪
사실 conic 이 바뀌어도 위 식은 성립함. 꼭 Circular Points 에 Dual 한 conic 이 아니어도 됨.
◦
따라서 cos⁡θ\cos\theta 도 invariant 하게 됨.

Metric Rectification: Recall

•
결국, 사전지식을 이용해 기존 이미지에서 수직인 직선 l,m{\rm l, m} 을 찾아 다음과 같은 식을 만들 수 있음.
l′TC∞∗m′=cos⁡90°=0{\rm l'}^T C^*_{\infty}{\rm m}' = \cos 90\degree = 0
•
Circual Point Dual Conic 의 변환된 conic 은 다음과 같이 표현됨을 앞에서 언급했음.
C∞∗ ′=[KKTKKTvvTKKTvTKKTv]C^*_{\infty}\ ' = \begin{bmatrix} {\rm K}{\rm K}^T & {\rm K}{\rm K}^T{\rm v} \\ {\rm v}^T{\rm K}{\rm K}^T & {\rm v}^T{\rm K}{\rm K}^T{\rm v} \end{bmatrix}
•
근데 이미 Affine Transform 이라는 가정이 있으니 v=0{\rm v} = 0 이고 다음과 같이 표현됨.
C∞∗ ′=[KKT00T0]=[s11s120s21s220000]C^*_{\infty}\ ' = \begin{bmatrix} {\rm K}{\rm K}^T & 0\\ 0^T & 0 \end{bmatrix} = \begin{bmatrix} s _{11} & s_{12} & 0\\ s _{21} & s_{22} & 0\\ 0 &0 & 0\\ \end{bmatrix}
•
결국 식은 다음을 푸는 것이 됨.
(l1′l2′l3′)[s11s120s21s220000](m1′m2′m3′)=0\begin{pmatrix} l_1' & l_2' & l_3' \end{pmatrix} \begin{bmatrix} s _{11} & s_{12} & 0\\ s _{21} & s_{22} & 0\\ 0 &0 & 0\\ \end{bmatrix} \begin{pmatrix} m_1' \\ m_2' \\ m_3' \end{pmatrix} = 0
◦
DLT 로 ss 를 구하고, S=KKTS=KK^T 를 Cholesky Decomposition 으로 구하면 결과적으로 기존에 언급했던 H{\rm H} 의 decomposition 에 따라 HA{\rm H}_A 를 최종적으로 구해낼 수 있음.
HA=[K00T1]{\rm H}_A = \begin{bmatrix} {\rm K} & 0 \\ 0^T & 1 \end{bmatrix}
◦
이렇게 구한 HA{\rm H}_A 를 inverse 해서 곱하면, Affine 요소를 제거하여 Similarity 로 변경할 수 있음.

Homography - Practical Applications

•
Automatically Building Panoramic Images
◦
SIFT descriptor 로 keypoint 를 찾고 Corresponding Points 를 찾음.
◦
Noisy 한 Corresponging Points 중 outlier 를 제거하기 위해 RANSAC 을 활용함.
◦
찾은 Corresponding Points 기반으로 DLT 를 사용함.