Duplicate

Lecture 10 | Perspective-n-Point

수강 일자
2023/02/27

Perspective-n-Point (PnP)

•
3D 나 2D Correspondences 를 이용해서 Camera Pose (R,tR, {\rm t} ) 를 구하는 것.
•
Intrinsic Parameter 를 알고 있는 상태 (Calibrated) 에서 Camera Pose 를 얻어내는 것이 일반적임.

Recall: With Known 3D-3D Correspondences

•
Projection Matrix P{\rm P} 를 구하기 위해서 6개의 corresponding points 와 DLT 알고리즘이 필요했음.
•
구한 P{\rm P} 를 decomposition 하여 K,R,tK, R, {\rm t} 를 구할 수 있었음.
•
다만, PnP 에서는 KK 를 알고 있기 때문에 이와 같은 방법을 사용하는 것이 비효율적임.

Decomposition with the Known K

•
이미 알고 있는 KK 를 활용해 R,tR, {\rm t} 를 구할 수 있음.
K[R∣t]≡[P1 P2 P3 P4]λ[R∣t]=K−1[P1 P2 P3 P4]λR=K−1[P1 P2 P3]=UDVT\begin{align*} &K[R | {\rm t}] \equiv [\rm P_1\ P_2\ P_3\ P_4] \\ &\lambda[R|{\rm t}] = K^{-1}[\rm P_1\ P_2\ P_3\ P_4] \\ &\lambda R = K^{-1 }[{\rm P_1\ P_2\ P_3}] = UDV^T \end{align*}
•
위 식에서, RR 은 rotational matrix 이기 때문에 SVD 를 하면 D=ID=I 임. 때문에 아래가 성립함.
R=UVTR = UV^T
•
λt=K−1P4\lambda{\rm t} = K^{-1}{\rm P}_4 인데, 앞선 식에서 기존 SVD 에서 diagnoal term d11d_{11} 이 RR 에서 빠졌기 때문에 (Up-to-Scale 이어서 rotational matrix 의 특성을 지키기 위해 나눠진 값) 이를 마찬가지로 나누어주어야 함.
t=1d11K−1P4{\rm t} = \frac{1}{d_{11}}K^{-1}{\rm P}_4

How to Compute R,tR, {\rm t} Given Known KK

•
KK 는 5DoF 이고 P{\rm P} 는 11DoF 이기 때문에 KK 를 알면 6DoF 만 남음.
•
이론적으로 3 Corresponding Points 만을 사용하면 R,tR, {\rm t} 를 구할 수 있음.
•
필요한 Corresponding Points 의 수 nn 에 따라서 PnP 로 명명함.
◦
P3P, P4P, PnP, EPnP (Efficient PnP) 등임.

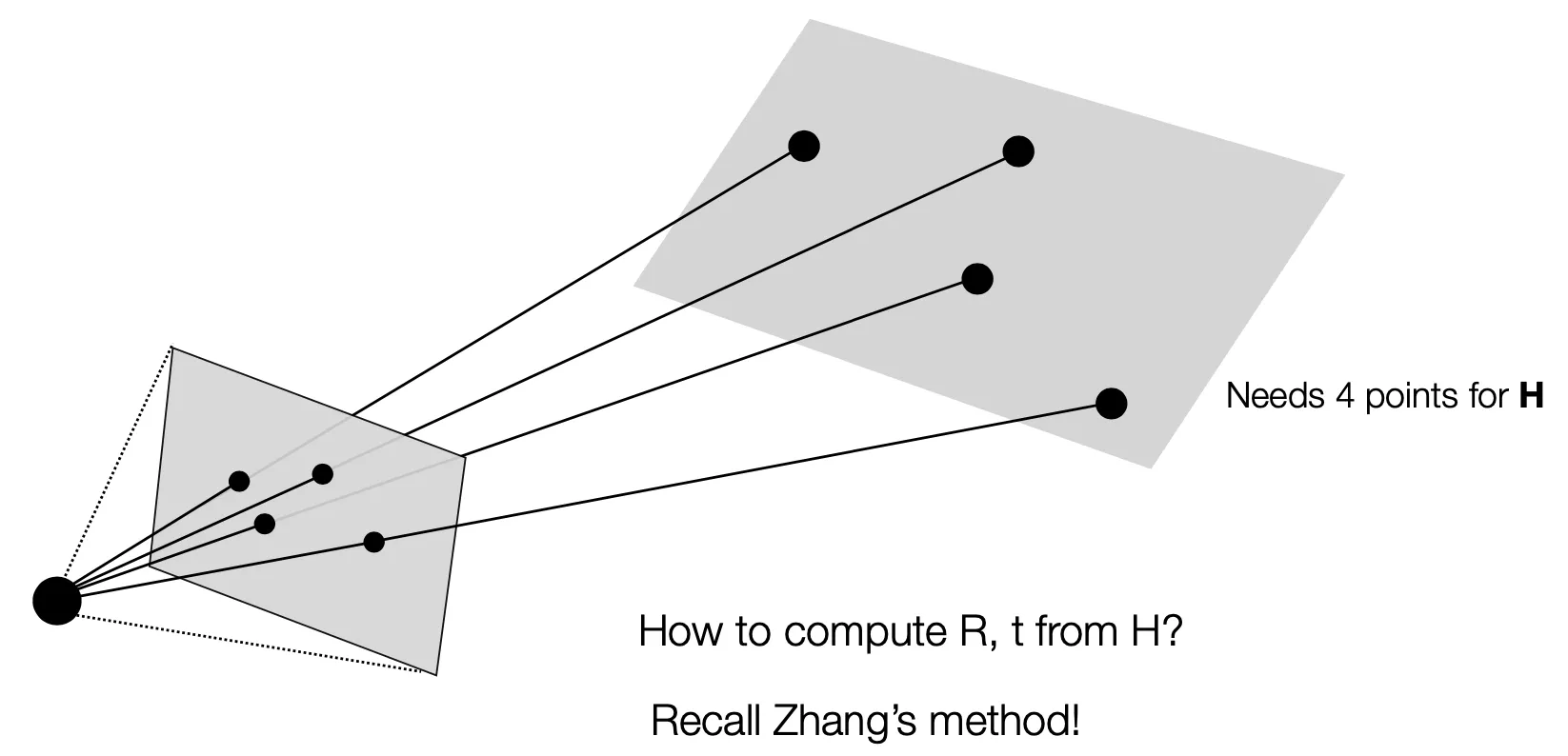
P4P (Planar Cases)

•
3D 와 2D 간 4 개의 Corresponding Points 를 알면 Homography H{\rm H} 를 계산할 수 있음.
•
H{\rm H} 로부터 R,tR, {\rm t} 를 구하는 것은 Zhang’s Method 에 따름.
◦
기존 Zhang’s Method 는 B=ω=K−TK−1{\rm B} = \omega = K^{-T}K^{-1} 을 구하기 위해서 3 개의 서로 다른 Homography 를 필요로 했는데, 여기선 KK 를 이미 알고 있으니 그럴 필요가 없음.
◦
KK 와 Homography H{\rm H} 를 알면, R,tR, {\rm t} 를 바로 구할 수 있었음.
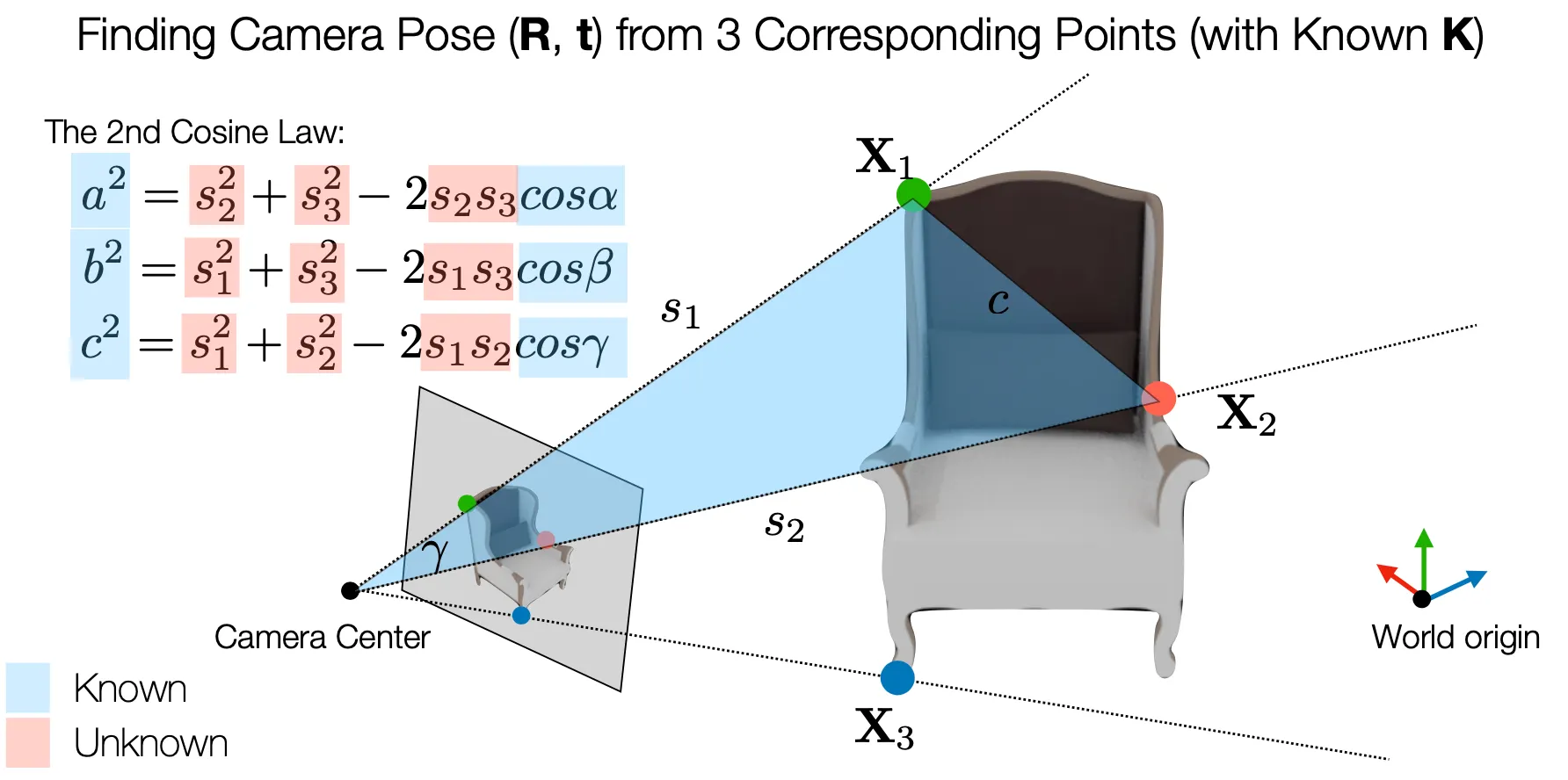
λK−1h1=r1λK−1h2=r2→r1=K−1h1∥K−1h1∥r2=K−1h2∥K−1h2∥r3=r1×r2\lambda K^{-1}{\rm h}_1 = r_1 \quad \lambda K^{-1}{\rm h}_2 = r_2 \\ \to r_1 = \frac{K^{-1}{\rm h}_1}{\|K^{-1}{\rm h}_1\|} \quad r_2 = \frac{K^{-1}{\rm h}_2}{\|K^{-1}{\rm h}_2\|} \quad r_3 = r_1 \times r_2
t=K−1h3λ=K−1h3∥K−1h1∥{\rm t} = \frac{K^{-1}{\rm h}_3}{\lambda} = \frac{K^{-1}{\rm h}_3}{\|K^{-1}{\rm h}_1\|}

P3P (General Cases)

•
3D 와 2D 간 3 개의 Corresponding Points 를 알면 Camera Pose (R,tR, \rm t) 를 계산할 수 있음.
•
a,b,ca, b, c 는 3D 대응점들 간의 거리를, α,β,γ\alpha, \beta, \gamma 는 대응점끼리의 연결선끼리 이루는 각도를 의미함.
•
a,b,ca,b,c 는 그냥 좌표간 euclidean distance 를 통해 쉽게 계산 가능하고, α,β,γ\alpha, \beta, \gamma 는 2D → 3D 의 reverse projection 기반의 식에서 KK 와 2D 상의 점들을 모두 알고 있기 때문에 아래처럼 계산이 가능함.
cos⁡θ=d1Td2d1Td1d2Td2=(K−1x1)T(K−1x2)(K−1x1)T(K−1x1)(K−1x2)T(K−1x2)=x1T(K−TK−1)x2x1T(K−TK−1)x1x2T(K−TK−1)x2=x1Tωx2x1Tωx1x2Tωx2\begin{align*} \cos\theta &= \frac{{{\rm d_1}^T{\rm d_2}}}{\sqrt{{\rm d_1}^T{\rm d_1}}\sqrt{{\rm d_2}^T{\rm d_2}}} = \frac{{(K^{-1}{\rm x_1})^T(K^{-1}{\rm x_2})}}{\sqrt{(K^{-1}{\rm x_1})^T(K^{-1}{\rm x_1})}\sqrt{(K^{-1}{\rm x_2})^T(K^{-1}{\rm x_2})}} \\ &= \frac{{\rm x_1}^T(K^{-T}K^{-1}){\rm x_2}}{\sqrt{{\rm x}_1^T(K^{-T}K^{-1}){\rm x_1}}{\sqrt{{\rm x}_2^T(K^{-T}K^{-1}){\rm x_2}}}} = \frac{{{\rm x_1}^T\omega{\rm x_2}}}{\sqrt{{\rm x_1}^T\omega{\rm x_1}}\sqrt{{\rm x_2}^T\omega{\rm x_2}}} \end{align*}
•
코사인 제 2법칙을 이용하면 카메라 중심점으로부터 3D 의 대응점 까지의 각 거리를 구할 수 있는데, 이를 기반으로 최종적인 Camera Ceneter 의 위치를 알 수 있음. (3D 대응점을 중심으로 하는 세 구의 교점 위치)
A4v4+A3v3+A2v2+A1v1+A0=0u=s2s1v=s3s1A_4v^4 + A_3v^3+A_2v^2 +A_1v^1 + A_0 = 0\\ u=\frac{s_2}{s_1} \quad v=\frac{s_3}{s_1}
◦
다만, 위 식은 4 개의 (s1,s2,s3)(s_1,s_2,s_3) 해 쌍들을 가지기 때문에 어떤 것이 답인지 명확하진 않음.
•
마찬가지 방법으로 3D 대응점이 아닌, 2D 대응점들에 대해서 동일하게 진행하면 구한 Camera Center 로부터 2D 대응점까지의 거리를 알 수 있고, Camera Rotation 정보도 알 수 있음.

PnP

•
3D 와 2D 의 N≫3N \gg 3 개의 대응점이 있는 경우에 Camera Pose 를 얻는 방법론임.
•
일반적으로 3D 상에 Non-Coplanar 한 4 개의 점 (Control Points) 을 선택하면, 나머지 모든 점들을 해당 4 개의 좌표의 weighted sum 형태로 표현할 수 있음.
Piw=∑j=14αijCjw←World CoordinateP_i^w = \sum_{j=1}^4 \alpha_{ij}C_j^w \larr {\rm World\ Coordinate}
◦
재미있는 점은, Camera Coordinate 로 바뀌어도 이 관계는 weight 가 동일하게 성립한다는 것임.
Pic=∑j=14αijCjc←Camera CoordinateP_i^c = \sum_{j=1}^4 \alpha_{ij}C_j^c \larr {\rm Camera\ Coordinate}
•
위 관계를 이용해서, Camera Coordinate 에서 3D → 2D projection 관계를 세워보면 Intrinsic Matrix KK 를 곱하는 형태가 되고, 다음과 같은 식을 얻을 수 있음.
wi[uivi1]=[fu0uc0fvvc001]∑j=14αij[xjcyjczjc]w_i \begin{bmatrix} u_i \\ v_i \\ 1 \end{bmatrix} = \begin{bmatrix} f_u & 0 & u_c \\ 0 & f_v & v_c \\ 0 & 0 & 1 \end{bmatrix} \sum_{j=1}^4 \alpha_{ij} \begin{bmatrix} x_j^c \\ y_j^c \\ z_j^c \\ \end{bmatrix}
◦
Up-to-Scale 의 식을 등호로 바꾸기 위해서 wiw_i 항목이 들어가 있는데, 마지막 항의 단순 비교를 통해 다음과 같이 wiw_i 를 구해낼 수 있음.
wi=∑j=14αijzjcw_i = \sum_{j=1}^4 \alpha_{ij}z_j^c
•
해당 식을 풀어서 쓰면 다음과 같이 두 개의 equation 을 얻을 수 있음.
∑j=14αijfuxjc+αij(uc−ui)zjc=0∑j=14αijfvyjc+αij(vc−vi)zjc=0\sum_{j=1}^4 \alpha_{ij}f_ux_j^c + \alpha_{ij}(u_c -u_i)z_j^c = 0 \\ \sum_{j=1}^4 \alpha_{ij}f_vy_j^c + \alpha_{ij}(v_c -v_i)z_j^c = 0 \\
•
최종적으로, World Coordinate 의 4 개의 Control Points 의 Camera Coordinate 대응점을 찾기 위해서 12 개의 unknown 으로 이루어진 12×112\times 1 vector 를 찾아내기 위한 DLT system 을 구축할 수 있으며 그러기 위해서는 최소 6개 이상의 대응점이 필요함.
•
DLT 를 통해서 Control Points 의 Camera Coordinate 대응점을 찾았으면, R,tR, \rm t 는 다음과 같이 reprojection error 를 최소화도록 찾을 수 있음.
(R,t)=arg min⁡R∈SO(d),t∈Rd∑i=1nwi∥(RPiw+t)−Pic∥(R, {\rm t}) = \argmin_{R \in SO(d), {\rm t} \in {\mathbb R}^d} \sum_{i=1}^n w_i \| (RP_i^w + {\rm t}) - P_i^c \|
◦
구체적인 최적화 방법론은 아직 다루지 않음.