Surface Representation for Point Clouds

리뷰 날짜
2022/09/17
분야
3D Model Representation
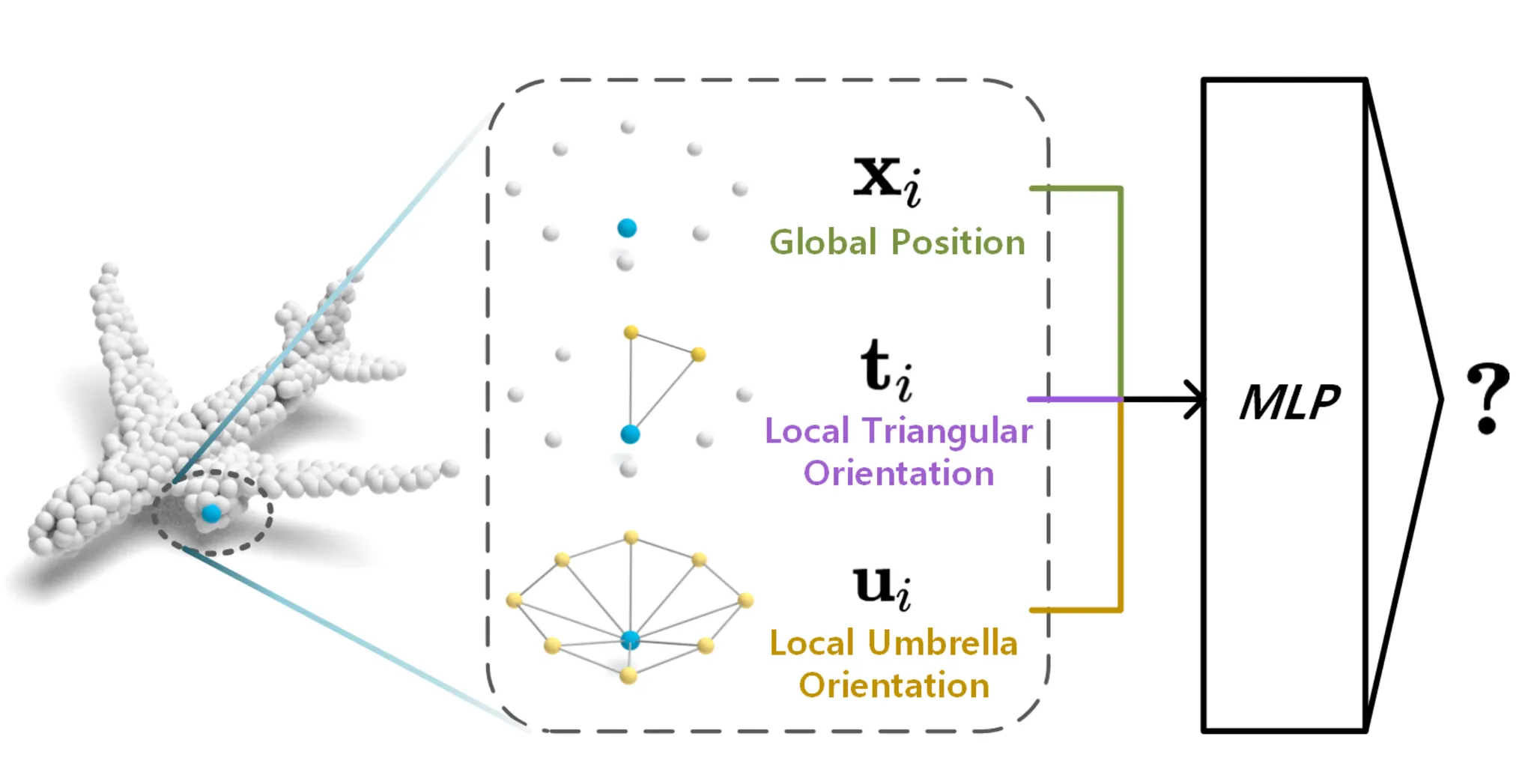
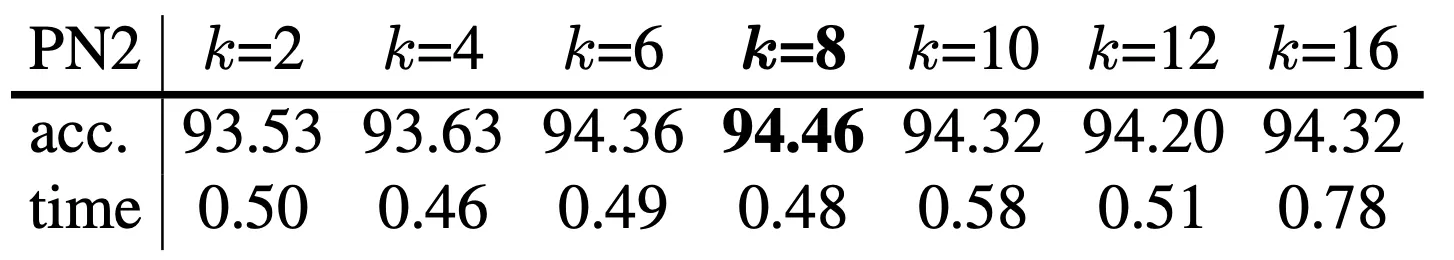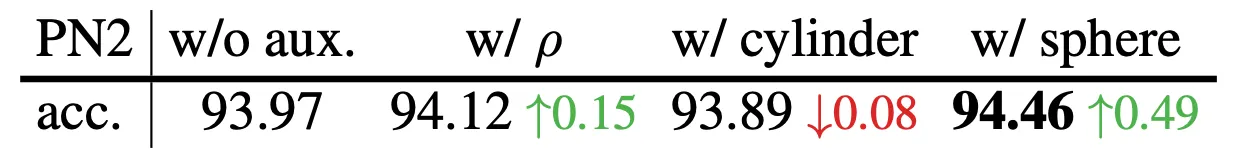본 포스트에서는 로컬 영역의 기하학적인 구조를 표현할 수 있는 Point Cloud 의 형태를 제시한 논문에 대해서 소개드리려고 합니다.
“Surface Representation for Point Clouds”
논문에 대한 내용을 직접 보시고 싶으신 분은 이곳을 참고하시면 좋습니다.

Objective

3D Scanner 등으로 얻어낸 날 것의 Point Cloud 들은 자율주행, 증강현실, 로보틱스 등 다양한 어플리케이션에서 활용될 수 있다는 측면에서 큰 이점을 가집니다. 하지만, 이러한 형태로 얻어낸 Point Cloud 데이터는 일반적으로 고르지 못한 탓 (논문에서 irregularity 라고 표현한 항목입니다. 개인적으로는 sparsity, surface alignment 등도 포함한 개념인 것 같습니다.) 에 활용되기 어려운 경우가 많습니다.
Overview of PointCloud Classificatrion with RepSurf
이러한 문제점을 해결하기 위해 PointNet 에서는 point-wise MLP 를 사용하여 각 점들로부터 독립적으로 학습한 값을 바탕으로 Point Cloud 의 전체적인 형태정보 (Global Information) 를 나타내는 Symmetric Function 을 얻어냅니다.
Symmetric Function? PointNet 에서 주요하게 해결하고자 했던 과제인 Permutation Invariance 를 해결하기 위해 설계한 구조로, 여러 입력 변수의 순서에 따라 상관없이 동일한 값이 나오는 함수를 의미합니다. Point Cloud 의 정렬 순서에 따라서 다른 분류 결과 등이 나오는 것을 방지하는 목적입니다.
PointNet 에 이어서 PointNet++ 에서는 Set Abstraction (SA) Layer 를 두어 Point Cloud 의 로컬 영역 구조에 대한 정보를 추출하려는 시도를 합니다. PointNet++ 에서 설계한 SA Layer 는 Point Cloud 에서 주요한 입력 점들을 추출하는 Sampling Layer, 주요한 입력 점들과 인접한 점들을 찾아 묶는 Grouping Layer, 그리고 마지막 PointNet Layer 에서 앞서 묶은 Grouping Layer 의 점들 정보를 바탕으로 로컬 영억의 feature vector 를 추출하는 형태로 구성되어 있습니다.
이처럼 많은 선행연구들이 Point Cloud 의 Irregularity 를 해결하기 위해 쓰여졌지만 이들의 방법론은 각각의 점들로부터 feature 들을 뽑아내는 형태에 그쳤고 방법론 자체가 3D 모델의 로컬영역에 대한 구조 정보를 이해한 채 진행되지는 않았습니다. 하지만 실제로 Point Cloud 를 사용하여 학습을 할 때 로컬영역에 대한 구조 정보는 굉장히 중요하고 몇몇의 선행연구들은 이를 해결하기 위해 Implicit 하게 로컬 영역에 대한 구조 정보를 얻어내는 방법론들을 다양하게 구상해냅니다. 하지만 이러한 방법론들은 대게 복잡한 전처리나 연산을 필요로 했고 중요한 정보를 놓치는 일들이 발생했습니다.
논문에서는 이러한 상황에서 기존 연구들과는 다르게 Explicit 하게 로컬 영역에 대한 구조 정보를 추가하는 방법론을 새롭게 구상하게 됩니다.

Background

논문에서는 기존의 Implicit 한 로컬 영역의 구조 정보 제공 방식에서 벗어나 Explicit 한 방법론을 구상합니다. 논문의 방법론을 이해하기 위해서 기본적인 Taylor Series 에 대한 이해가 필요합니다.
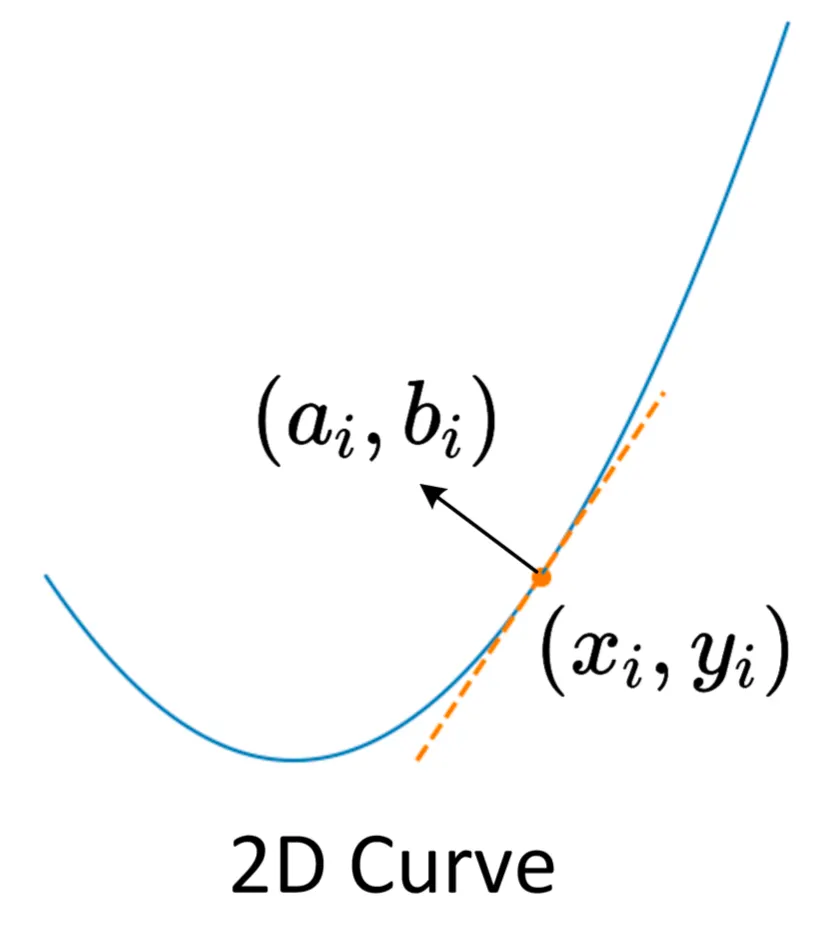
먼저, 일반적인 2D Curve 상에서의 점 (t,f(t))(t,f(t)) 에서의 Taylor Series 는 아래와 같이 표현할 수 있습니다.
f(x)=∑n=0∞f(n)(t)n!(x−t)n, ∣x−t∣<ϵf(x) =\sum_{n=0}^\infty \frac{f^{(n)}(t)}{n!}(x-t)^n, \ |x-t| < \epsilon
이는 많은 분들이 이미 아시다싶이 (t,f(t))(t,f(t)) 를 지나면서 해당 점에서의 n 차 미분값이 모두 동일하도록 급수를 만든 것입니다. 논문에서는 실제 계산에 이를 사용하기 위해 이를 간결하게 1차 미분값까지만 사용하게 됩니다.
f(x)≃f(t)+f′(t)(x−t)f(x) \simeq f(t) + f'(t)(x-t)
논문에서는 위 식의 f(t)f(t) 를 점 (t,f(t))(t,f(t)) 근처의 Global Position, f′(t)f'(t) 를 점 (t,f(t))(t,f(t)) 근처의 Local Orientation 으로 바라볼 수 있다고 제안합니다. Local Orientation 을 지정한 것은 로컬 영역 구조 정보를 얻어내기 위해서 3D Model 을 이루는 표면에 대한 정보를 포함하기 위해 접선 방향의 성분을 구하려는 시도를 했다고 이해하시면 됩니다.
Local Shape Representation
2D 상에서는 위 그림과 같이 로컬 영역 구조 정보를 얻어낼 수 있고, 논문에서는 2D Curve 상에서 Local Orientation 정보를 아래와 같이 2D Plane 으로 나타냅니다.
ai(x−xi)+bi(y−yi)=0aix+biy−(aixi+biyi)=0a_i(x-x_i) + b_i(y-y_i) = 0\\ a_ix+b_iy - (a_ix_i+b_iy_i) = 0
위 식에서 (ai,bi)(a_i,b_i) 는 특정 점에서의 법선 방향 단위벡터이며 xi=tx_i=t, yi=f(t)y_i=f(t), aibi=−f′(t)\frac{a_i}{b_i}=-f'(t) 로 나타낼 수 있습니다. 이러한 상황에서 논문에서는 Local Curve 에 대한 정보를 다음과 같이 기술합니다.
ci=(xi,yi,ai,bi,aixi+biyi)c_i=(x_i,y_i,a_i,b_i,a_ix_i+b_iy_i)
정리하자면, 논문에서 치중하는 바는 로컬 영역의 구조 정보는 결국 국소 영역에서 3D Model 이 어떤 형태를 가지는지를 정확하게 기술하는 것이며 이를 위해서는 3D Model 이 작은 범위 내에서 어떠한 표면을 가지는지를 알아야 하고 결과적으로 이는 표면의 법선 벡터 방향을 정확히 아는 것이라고 보는 것입니다. 그리고 이러한 법선 벡터 정보, 점들의 정보, 그리고 원점에서 평면까지의 거리 정보를 합쳐서 최종적인 로컬 영역에 대한 정보라고 정의하게 됩니다.

Method: RepSurf

3D 컴퓨터 그래픽스에서 3D Model 을 표현하는데 가장 일반적인 표현 방법은 Triangle Mesh 입니다. 이는 표현하고자 하는 물체를 점 (Vertex) 와 이 점 3개가 모여서 생성한 면 (Face)로 표현하는 방법으로, 연속적이고 복잡한 3D Shape 를 유연하게 표현할 수 있습니다. 하지만, Point Cloud 데이터는 일반적으로 면에 대한 정보를 가지고 있지 않기 때문에 Triangle Mesh 데이터로의 직접적인 변환이 불가능하고, 억지로 진행하더라도 그 순서에 따라서 형태가 달라지기 때문에 계산을 필요로 하고 이러한 계산을 거치더라도 부자연스러운 부분들의 형성으로 Point Cloud 가 가지고 있던 특징들을 잃을 수도 있습니다.
논문에서는 이러한 상황에서 Irregularity 를 보유한 Point Cloud 가 Traingle Mesh 에 비해서 로컬 영역에 대한 정보가 부족한 문제점을 해결하는 형태로 접근합니다. 이 접근으로 제안하게 된 3D Model 의 표현 방법이 논문에서 이야기하는 RepSurf 이며 이는 다음과 같은 특징들을 가지도록 설계되었습니다.
1.
Discreteness Point Cloud 의 각 점들이 각각 하나씩의 RepSurf feature 를 가지도록 합니다.
2.
Explicit Locality 로컬 영역 구조 정보를 Explicit 하게 표현할 수 있도록 합니다.
3.
Curvature Sensitivity Edge 와 Local Shape 를 직관적으로 드러낼 수 있도록 합니다.
아래에서는 실제로 논문에서 제시한 RepSurf 가 어떠한 형태로 설계되었는지를 보여줍니다.

Triangular RepSurf

앞선 Background 에서 2D Curve 상에서 로컬 영역 구조 정보를 표현하는 방법에 대해서 알아보았습니다. Triangular RepSurf 에서는 앞에서 이야기한 내용을 3D 로 확장하여 비슷하게 반복합니다.
Pytorch-Style Pseudocode of Triangular RepSurf
위 pseudocode 를 순서대로 정성적으로 설명하면 다음과 같습니다.
1.
Point Cloud 데이터 X={x1,...,xn}⊆RN×3X=\{x_1, ..., x_n \} \sube \mathbb{R}^{N\times3} 에 대해서 각각 최근접 2개의 점들을 찾습니다.
2.
앞에서 찾은 2개의 점의 중앙을 Centroid 라고 칭하며 새로운 점들로 지정합니다.
3.
처음 점과 그 점의 해당하는 최근접 2개의 점들 사이의 거리 벡터의 외적으로 Centroid xi=(xi,yi,zi){\rm{x}}_i= (x_i, y_i,z_i) 에 대한 Normal Vector vi=(ai,bi,ci)v_i = (a_i, b_i, c_i) 를 얻어냅니다.
4.
Normal Vector 의 방향에 크게 두 가지가 있을 수 있는데, (표면 안쪽, 표면 바깥쪽) 논문에서는 Normal Vector 의 첫 번째 항이 양수가 되도록 먼저 값을 구하고, 50% 확률로 부호를 바꾸도록 설계합니다.
5.
Normal Vector 와 Centroid 의 Product Sum 을 통해 Surface Position 을 구합니다. 이는 원점으로부터 접선 평면까지의 거리를 의미하기도 합니다. 이 때 각 좌표가 [−1,1][-1,1] 사이의 범위를 가지는 Point Cloud 에서 Surface Position 의 범위는 [−3r,3r][-\sqrt3 r, \sqrt3 r] 이기에 3\sqrt3 으로 나누어 normalize 시켜준 것을 보실 수 있습니다.
6.
이렇게 구해낸 Centroid, Normal Vector, Surface Position 정보를 묶어 로컬 영역 구조 정보를 완성합니다.
5 번에 대한 약간의 부연설명을 하자면, 특정한 Centroid 와 그에 해당하는 Normal Vector 가 주어졌을 때 해당 Centroid 를 지나는 Surface 는 다음과 같이 나타내어집니다.
ai(x−xi)+bi(y−yi)+ci(z−zi)=0aix+biy+ciz−(aixi+biyi+cizi)=0a_i(x-x_i)+b_i(y-y_i)+c_i(z-z_i)=0 \\ a_ix+b_iy+c_iz-(a_ix_i+b_iy_i+c_iz_i) = 0
이 때 점으로부터 평면까지의 거리 공식을 적용하여 원점으로부터 위 평면 사이의 거리를 구하게 되면 aixi+bixi+ciziai2+bi2+ci2\frac{a_ix_i+b_ix_i+c_iz_i}{\sqrt{a_i^2+b_i^2+c_i^2}} 형태가 되는데 법선벡터가 단위벡터이기 때문에 이는 곧 pi=aixi+bixi+cizip_i=a_ix_i+b_ix_i+c_iz_i 와 같고 Normal Vector 와 Centroid 의 Product Sum 형태인 것입니다.
논문에서는 최종적으로 이렇게 얻어낸 Normal Vector 와 Surface Position 를 묶어 ti=(ai,bi,ci,pi)t_i=(a_i,b_i,c_i,p_i) 로 구성하여 한 점에서의 Triangular RepSurf 를 정의하고 이를 전체 점으로 확장하여 다음과 같이 Triangluar RepSurf 를 완성합니다.
T={t1,...tn}⊆RN×4T = \{ t_1, ...t_n\} \sube \mathbb{R}^{N\times4}

Umbrella RepSurf

Triangular RepSurf 를 계산할 때는 최근접 2개의 점을 사용하여 Centroid 를 구하고 해당 Centroid 에 할당할 Normal Vector 를 구해냈습니다. 하지만 최근접 2개의 점으로 로컬 영역 구조 정보를 구성할 경우 불안정한 Local Representation 이 등장하는 경우들이 있었고 이를 해결하기 위해서 논문에서는 각 점마다의 로컬 영역에 대한 범위를 확장하는 시도를 합니다.
PyTorch-Style Pseudocode of Umbrella RepSurf
위 pseudocode 를 순서대로 정성적으로 설명하면 다음과 같습니다.
1.
Point Cloud 데이터 X={x1,...,xn}⊆RN×3X=\{x_1, ..., x_n \} \sube \mathbb{R}^{N\times3} 에 대해서 각각 최근접 K개의 점들을 찾습니다.
2.
앞에서 찾은 K개의 최근접 점들을 위치에 따라서 반시계방향으로 정렬합니다. 이는 zz 좌표를 고려하지 않고 xyxy plane 상에서 반시계방향으로 순서가 위치할 수 있도록하는 과정입니다.
3.
정렬한 K개의 최근접 점들 각각에 대해서 순서에 맞게 쌍을 지정해 Triangle 을 만들어주기 위해서 기본의 K 개의 최근접 점들의 순서를 한 칸씩 땡긴 순서와 기존 순서를 쌍을 지어줍니다.
4.
앞에서 찾은 쌍의 중앙을 Centroid 라고 칭하며 새로운 K 개의 점들로 지정합니다.
5.
처음 점과 해당하는 최근접 2개의 쌍들 사이의 거리 벡터의 외적으로 Normal Vector 를 얻어내고 normalize 하는 과정을 진행합니다.
6.
각 Centroid 별로 생성된 Normal Vector 의 첫 번째 항이 양수가 되도록 먼저 값을 구하고, 50% 확률로 부호를 바꿉니다.
7.
Normal Vector 와 Centroid 의 Product Sum 을 통해 Surface Position 을 구합니다.
8.
이렇게 구해낸 Centroid, Normal Vector, Surface Position 정보를 묶어 로컬 영역 구조 정보의 기본적인 내용을 완성합니다.
9.
앞서 완성한 로컬 영역 구조 정보를 transform 대신 학습이 가능한 MLP T\mathcal{T} 에 넣어 최종적인 로컬 영역 구조 정보를 나타내는 feature 를 추출합니다.
논문에서는 최종적으로 위의 과정을 통해 다음과 같이 Umbrella RepSurf 를 완성합니다.
ui=A({T([x′ij,tij]),∀j∈{1,...,K}})u_i={\mathcal A}(\{{\mathcal{T}}([{\rm x'}_{ij}, {\rm t}_{ij}]), \forall j \in \{1, ..., K \}\})
위 식에서 xij′{\rm{x}}'_{ij} 는 Centroid xi{\rm{x}}_i 의 normalized 된 항이며, 정성적으로는 앞선 Triangular RepSurf 에서는 2개의 최근접 점들만을 이용해 하나의 작은 삼각형 면에 대응되는 Centroid 와 Normal Vector 그리고 Surface Position 을 구해냈다면 Umbrella RepSurf 에서는 K 개의 최근접 점들을 이용해 K 개의 삼각형 면에 대응되는 K 개의 Centroid, Normal Vector, 그리고 Surface Position 을 얻어내고 이들 정보를 MLP 를 이용해 변환하고 이들 모드를 묶어 (위 식의 aggregation 항목인 A\mathcal{A} 입니다.) 하나의 로컬 영역에 대한 값을 정의하게 되는 것입니다.
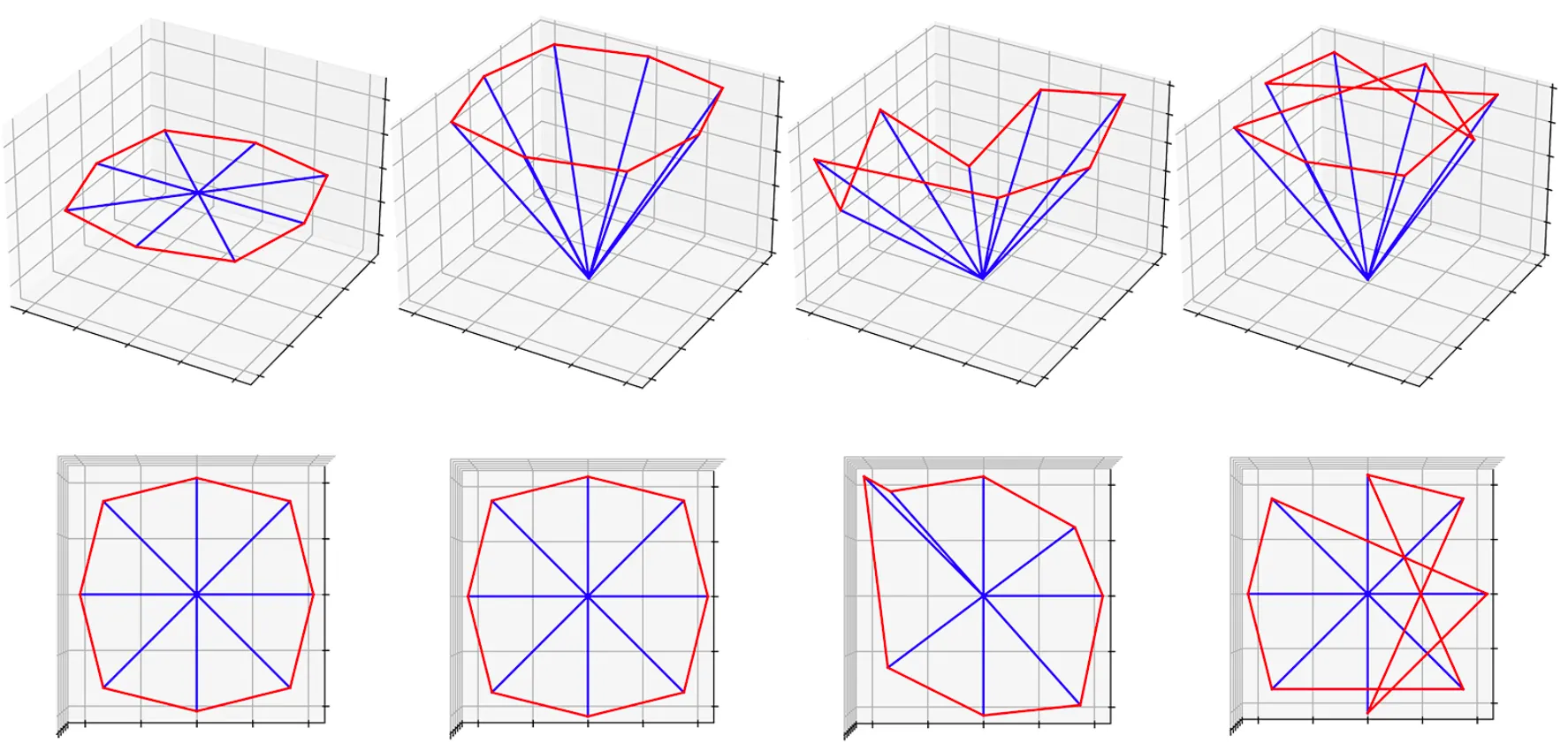
위 그림은 논문의 Umbrella RepSurf 방법론을 통해서 찾게 된 K 개의 삼각형 면들을 도식화한 것입니다. 논문의 방법론은 기존의 Umbrella Curvature 와는 다르게 두 번째 항목처럼 Homogenous 한 주변 점들을 가지는 경우 뿐만 아니라 세 번째 항목처럼 Heterogenous 한 주변 점들을 가지는 경우에도 잘 동작함을 보여주었습니다. 그림의 네 번째 항목은 반시계방향의 정렬과정을 하지 않은 경우로 Surface 에 대한 표현이 잘 드러나지 않음을 볼 수 있습니다.

Implementation

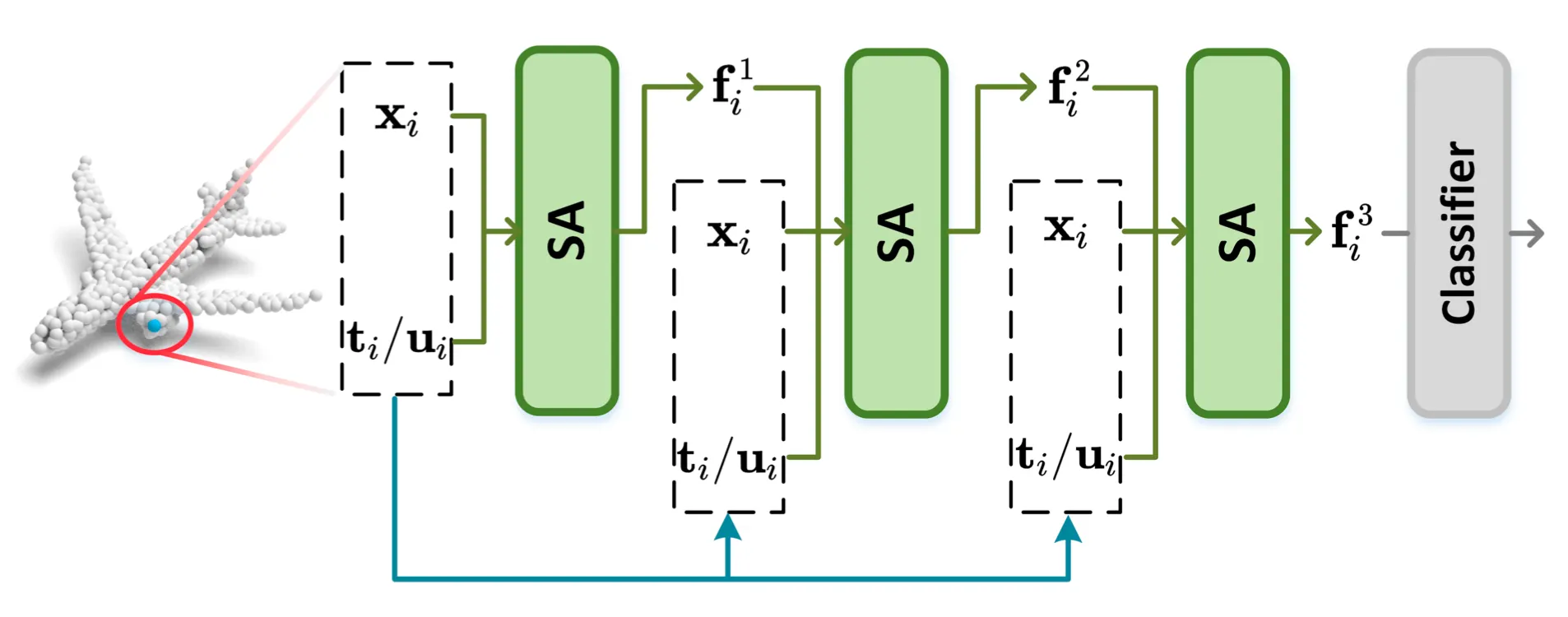
논문에서는 Single-Scale Grouping 을 사용하는 버전의 PointNet++ 에 RepSurf 를 적용하여 보았다고 합니다. PointNet++ 에서 로컬 영역 구조 정보 추출을 위해 설계된 Set Abstraction Layer 사이에 논문에서 설계한 Explicit 한 정보들을 추가로 넣어주는 형태의 구조를 설계한 것입니다.
An Overview of the Input Flow
위 그림의 xi{\rm x}_i 는 Point Cloud 의 좌표를, tit_i 와 uiu_i 는 각각 해당 좌표에 해당하는 Triangular RepSurf 와 Umbrella RepSurf 입니다. fijf_i^j 들은 특정 좌표 xi{\rm x}_i 의 jj 번째 feature 라고 보시면 됩니다. 기존의 구조와는 다르게 지속적으로 구해낸 RepSurf 정보를 학습에 활용함을 볼 수 있습니다. 하지만 논문에서는 단순히 이렇게 추가적인 정보를 제공하여 학습을 하는 것에 그치지 않고 성능을 끌어올릴 수 있는 기술들을 고안합니다.

Polar Auxillary

간단하다는 측면에서 많은 Point Cloud 기반의 모델들이 입력으로 직교 좌표계를 사용하지만, Centroid 와 그 최근접 점들간의 관계를 세밀하게 기술하기는 어렵습니다. 논문에서는 각 좌표를 원점으로부터의 거리와 각도를 기반으로 나타내는 극 좌표계를 사용해 거리와 방향성에 대한 세밀한 정보를 제공해줄 수 있을 것이라는 기대를 했고 추가적으로 도입하게 됩니다.
xij′=(xij′,yij′,zij′,ρij,θij,ϕij){\rm x}'_{ij}=(x'_{ij},y'_{ij},z'_{ij}, \rho_{ij}, \theta_{ij},\phi_{ij})
위 식은 실제로 특정 점 xi{\rm x}_i 의 최근접 점들을 기술할 때 직교 좌표계 뿐만 아니라 극좌표계에서의 해당 값들도 추가하려고 할 때 사용한 것입니다. 극 좌표계에서의 특징들로 인해 ρij=xij′2+yij′2+zij′2\rho_{ij}=\sqrt{x'^2_{ij} + y'^2_{ij} + z'^2_{ij}}, θij=arccos⁡zij′ρij\theta_{ij}=\arccos\frac{z'_{ij}}{\rho_{ij}}, ϕij=arctan⁡(yij′,xij′)\phi_{ij}=\arctan(y'_{ij},x'_{ij} ) 등이 성립합니다.

Channel Dedifferentiation

논문에서는 여러 종류의 데이터 (ex. Coordinate, Normal Vector, Surface Position, Point Features) 등을 입력으로 사용하는데 이렇게 형태가 다른 데이터들은 그 분포에 큰 차이가 있다는 것을 깨달았습니다. 이렇게 다른 형태의 입력들을 균등한 가중으로 취급하고 안정적으로 학습하기 위해서 논문에서는 Post-CD (linear function 을 거친 이후에 batch normalization 을 진행하는 방법) 를 Channel Dedifferntiation 방법론으로 사용합니다.

Experiment

논문에서는 그들이 제시한 Triangular RepSurf 와 Umbrella RepSurf 를 평가하기 위해 Classification, Segmentation, Detection task 를 설계합니다. 더불어 각각의 세부 설계들의 효과를 입증하기 위해 Ablation Study 또한 보여줍니다.

Classification

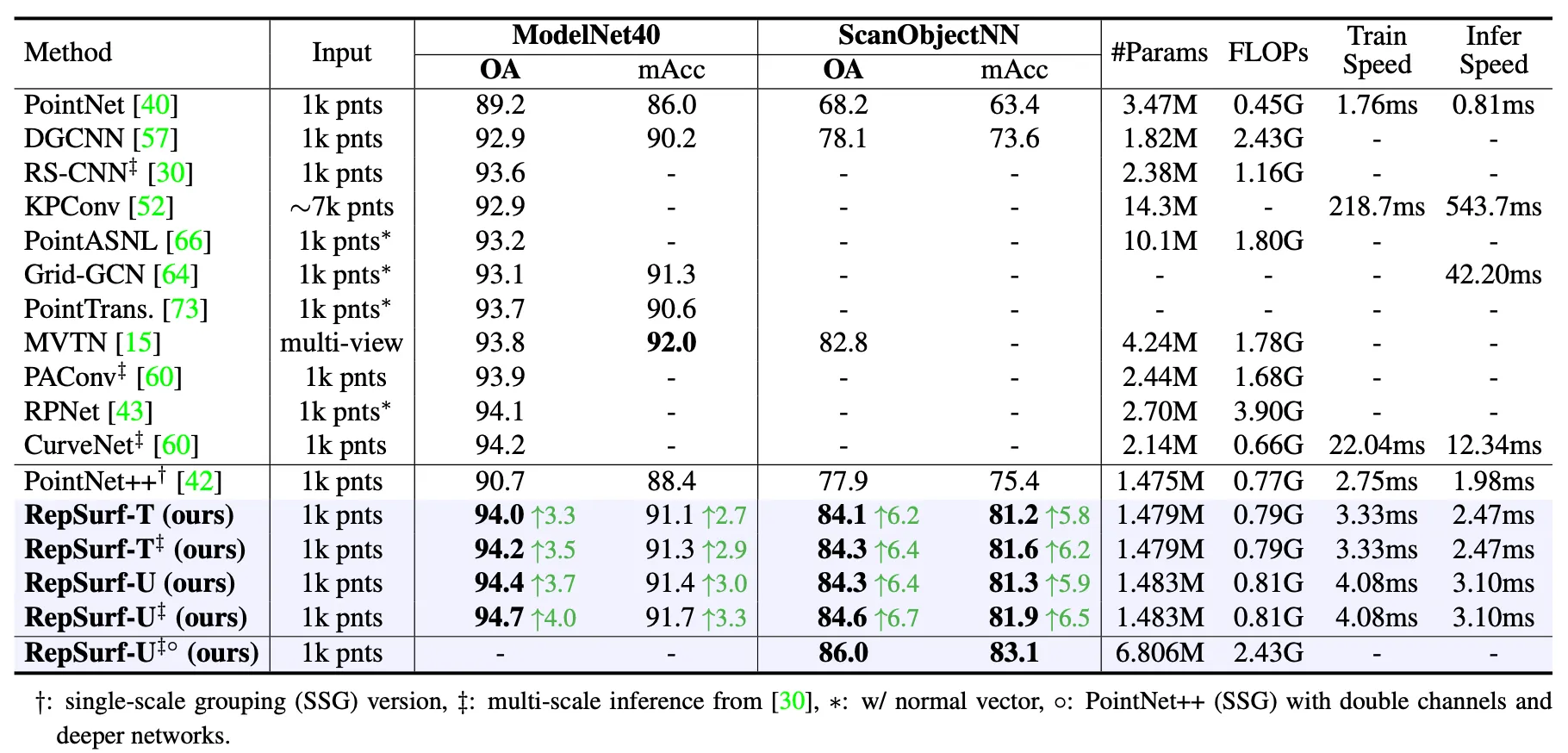
3D Object Classification 은 3D Model 로부터 특징을 추출하여 진행하는 가장 기초적인 task 입니다. 논문에서는 인간이 커스텀하게 제작한 데이터셋인 ModelNet40 과 실제 장면들로부터 얻어낸 ScanObjectNN 데이터셋을 사용하여 실험을 진행합니다.

Human-made Object Classification

ModelNet40 은 40 개의 카테고리로 나누어진, 9843 개의 training data 와 2468 개의 test data 로 구성된 데이터셋입니다. 아래의 표는 Triangular RepSurf 와 Umbrella RepSurf 를 ModelNet40 과 ScanObjectNN 에 대해서 평가한 것입니다.
Performance of Classification on ModelNet40 and ScaObjectNN
Triangular RepSurf 를 적용한 RepSurf-T 는 기존의 Single Scale Grouping 버전의 PointNet++ 에 비해서 3.7% 의 accuracy 향상이 있었고, Umbrella RepSurf 를 적용한 RepSurf-U 는 동일한 비교대상 기준으로 4.1% 의 accuracy 향상이 있었습니다. RS-CNN, PAConv, CurveNet 과 동일한 선 상에서 비교하기 위해서 논문에서도 Multi-Scale Inference 를 진행하여 정확도를 더 높여본 결과 최대 94.7% 까지 accuracy 를 끌어올릴 수 있었다고 합니다. 이는 같은 Multi-Scale Inference 를 진행한 비교대상들 중 가장 높은 수치를 보였던 CurveNet 보다 0.5% 높은 수치입니다. Accuracy 뿐만이 아니라 RepSurf-U 는 PointNet++ 를 기반으로 개선한 탓에 CurveNet 보다 학습 및 추론 속도가 각각 5.4 배, 4.0 배 빠르다는 이점도 있다고 합니다.

Real-World Object Classification

ModelNet40 에서 94.7% 까지 끌어올려 Saturation 의 범위까지 올라간 정확도 때문에 논문에서는 어려운 데이터셋에서 논문의 방법론이 어떻게 동작하는지도 실험해서 보여줍니다. 이를 위해서 SacnObjectNN 의 가장 어려운 종류로 알려진 PB_T50_RS 를 실험에 사용합니다. 이는 15 개의 카테고리로 구성된 2902 개의 데이터로 구성된 데이터셋입니다.
앞선 Human-made Object Classification 의 네 번째 열이 SacnObjectNN 데이터셋 기반의 실험 결과입니다. RepSurf-T 와 RepSurf-U 가 각각 84.3% 와 84.6% 의 accuracy 를 기록하면서 동일한 데이터셋으로 실험을 진행한 선행연구들 중 SOTA 였던 MVTN 을 1.5% 와 1.8% 정도 능가하는 것을 보여주었습니다. 더불어 논문의 방법론은 PointNet++ 를 기반으로 개선한 탓에 MVTN 보다 1.8 배 적은 수의 parameter 를 사용하고 연산 수도 1.2 배 적었다고 합니다.

Segmentation

Scene Segentation 은 일반적으로 outlier 나 noise 때문에 Classification 에 비해서 어려운 task 입니다. 논문에서는 RepSurf 를 평가하기 위해 S3DIS 와 ScanNet V2 데이터셋을 사용하게 됩니다.

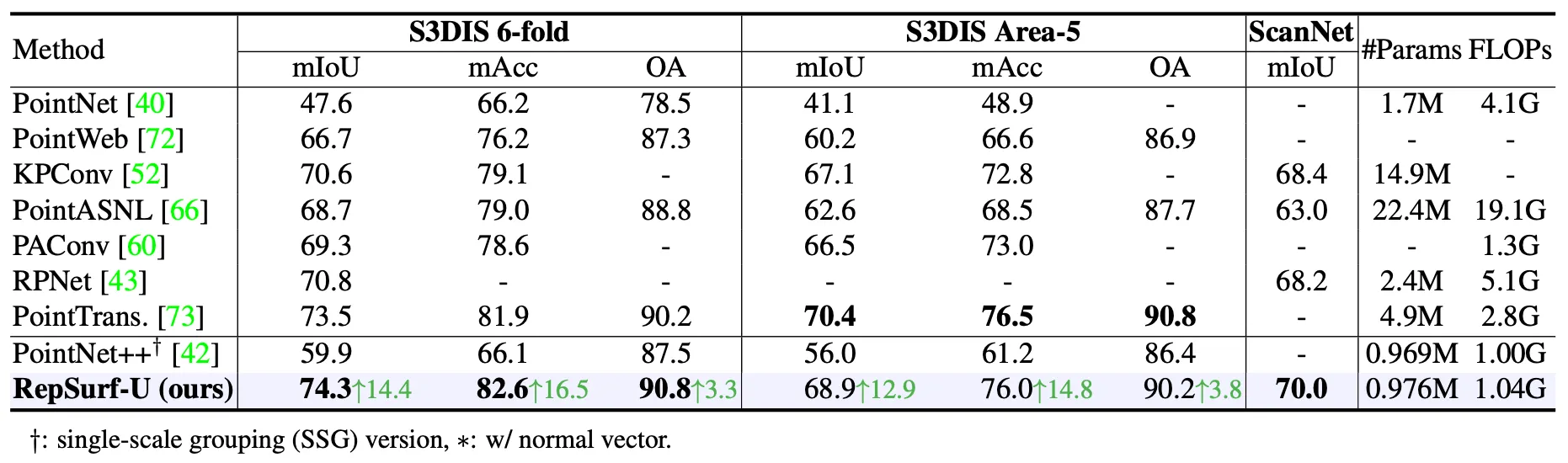
Semantic Segmentation on S3DIS

S3DIS 는 6 개의 indoor 영역에 대한 271 개의 장면들로 구성된 데이터셋입니다. 각각의 장면들은 총 13 개의 semantic label 로 카테고리화 되어 있습니다.
Performance of Semantic Segmentation
위 표는 S3DIS 데이터셋을 6-fold Cross Validation 로 나누어 학습한 것과 Area-5 에 대해서만 진행한 경우를 나누어 표현한 것입니다. 6-fold 와 Area-5 각각에 대해서는 논문의 RepSurf-U 가 개의 대상이었던 PointNet++ 에 비해서 14.4% 와 12.9% 높은 mIoU 를 보여주었습니다. 그 뿐만 아니라 6-fold 는 SOTA 였던 Point Transformer 를 0.8% 로 능가하였으며 Area-5 에서는 이기지는 못했지만 충분히 경쟁력 있는 결과를 보여주었습니다. 동시에 PointNet++ 를 기반으로 개선한 탓에 Point Transformer 보다 4.0 배 적은 parameter 를 사용하고 연산 수도 1.7 배 적었다고 합니다.

Semantic Segmentation on ScanNet

ScanNetV2 는 21 개의 카테고리로 나누어진, 1513 개의 indoor training data 와 100 개의 test data 로 구성된 데이터셋입니다.
앞선 Semantic Segmentation on S3DIS 의 네 번째 열이 ScanNet 데이터셋 기반의 실험 결과입니다. RepSurf-U 가 동일한 데이터셋을 사용한 것들 중 SOTA 였던 KPConv 를 1.6% 능가하는 mIoU 를 보여주었고 그 와중에 PointNet++ 를 기반으로 개선한 탓에 KPConv 보다 14.3 배 적은 parameter 를 사용했다고 합니다.

Detection

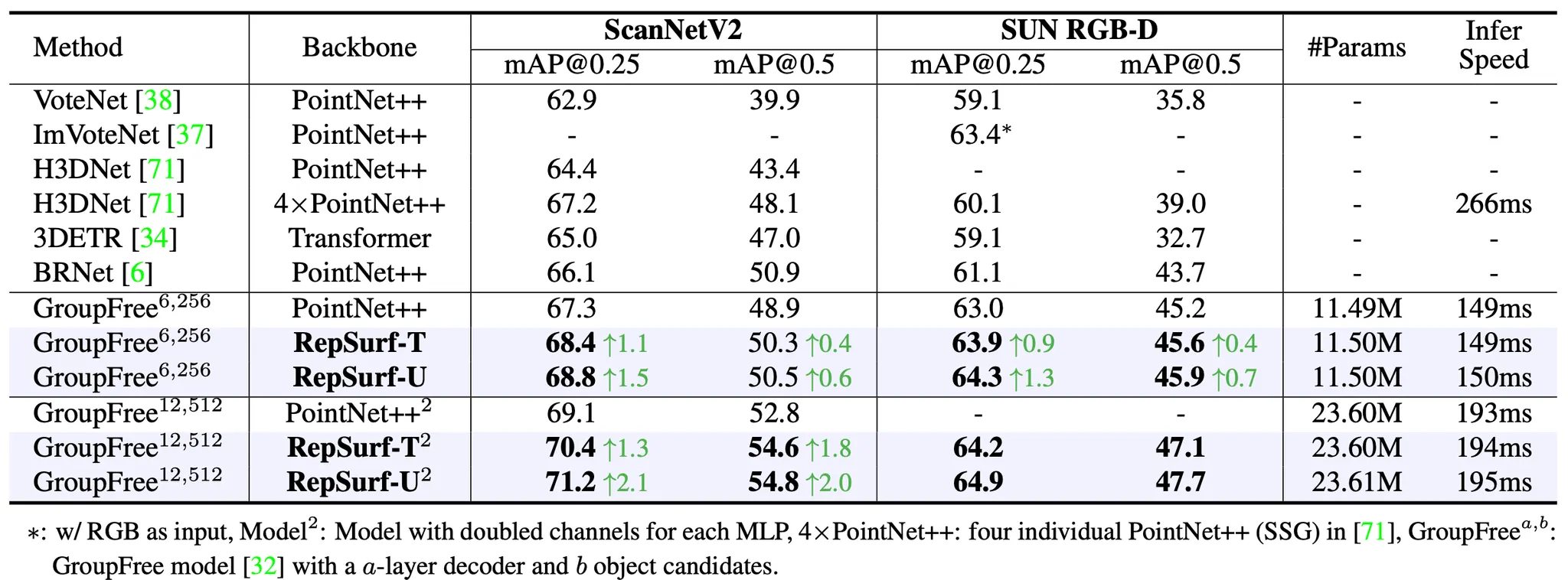
논문에서는 3D detection task 가 논문의 방법론이 어플리케이션 단에서의 우월함을 보여주는 분야라고 말합니다. 그들은 3D Detection task 에서 방법론을 평가하기 위해 널리 쓰이는 3D Object Detection 데이터셋인 ScanNet V2 와 SUN RGB-D 를 활용합니다.

Detection on ScanNet

ScanNet V2 는 18 개의 카테고리로 나누어진, 1513 개의 indoor scene 으로 구성된 데이터입니다. 논문에서는 물체로 인식하기 위한 threshold 를 0.25 일때와 0.5 일때를 나누어 실험 결과를 제시합니다.
Performance of Object Detection on ScanNet V2 and SUN RGB-D
위 표에서 보는 것처럼 RepSurf-U 는 거의 computation cost 의 증가 없이도 SOTA 였던 PointNet++ 가 적용된 GroupFree 에 비해서 mAP@0.25 에서 2.1% 의 mAP 증가를, mAP@0.5 에서 2.0% 의 mAP 증가를 보여주었습니다.

Detection on SUN RGB-D

SUN RGB-D 데이터셋은 3D Scene Analysis 를 위한 단일 뷰 RGB-D 데이터셋으로, 5000 개 가량의 inoor RGB 와 Depth 데이터로 구성되어 있습니다. 논문에서는 VoteNet 에서 구성한 설계를 가져와 SUN RGB-D 에서 10 개의 일반적인 카테고리를 뽑아서 실험을 진행했습니다.
앞선 Detection on ScanNet 의 네 번째 열이 SUN RGB-D 데이터셋 기반의 실험 결과입니다. RepSurf-U 는 PointNet++ 가 적용된 GroupFree-6,256 (6 개의 encoder layer 를 가지고 256 개의 물체 카테고리를 가지는 버전) 을 mAP@0.25 에서 1.3% 만큼, mAP@0.5 에서 0.6% 만큼을 능가했습니다. 더불어 RGB 입력 없이 GroupFree-12,512 에 RepSurf-U 를 적용한 버전은 현재 SOTA 인 ImVoteNet 을 mAP@0.25 에서 1.5% 가량 능가했습니다.

Ablation Study

논문에서는 Ablation Study 를 위해 다양한 형태의 구성을 설계합니다.

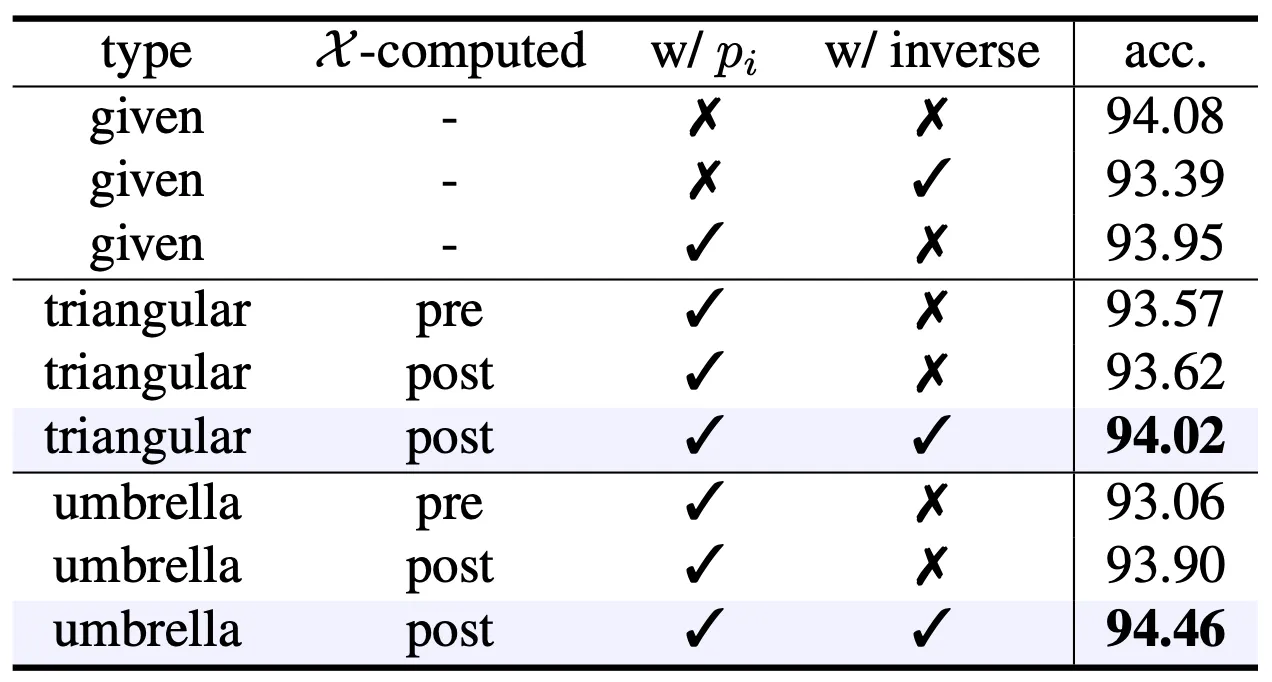
Types of RepSurf

아래의 표는 논문에서 Ablation Study 를 진행할 때 사용한 다양한 형태의 구성을 나타냅니다.
Ablation Study on the Types of RepSurf
먼저 type\rm{type} 은 입력의 종류를 나타내며, 기본적으로 Coordinate 및 Normal Vector 만 포함하는 given 과 논문에서 설계한 Triangular RepSurf, Umbrella RepSurf 로 나누어집니다.
다음으로 X−computed\mathcal{X}-\rm{computed} 는 RepSurf 를 얻어내는 시점을 의미합니다. 일반적으로 RepSurf 를 입력 Point Cloud 를 sampling 하기 전 high resolution 상에서 구해내지만, 경험적으로 sampling 이후에 구해내는 것이 더 좋음을 밝혀냈습니다.
마지막으로 w/pi{\rm w}/p_i 는 RepSurf 안에 Surface Position 에 대한 정보 pip_i 의 포함 여부이며 w/inverse{\rm w}/{\rm inverse} 는 RepSurf 를 구하는 과정에서 설계한 50% 확률의 Normal Vector 의 부호 변경 과정의 포함 여부입니다. 이 과정은 각각 약간씩 accuracy 를 높임을 알 수 있었습니다.

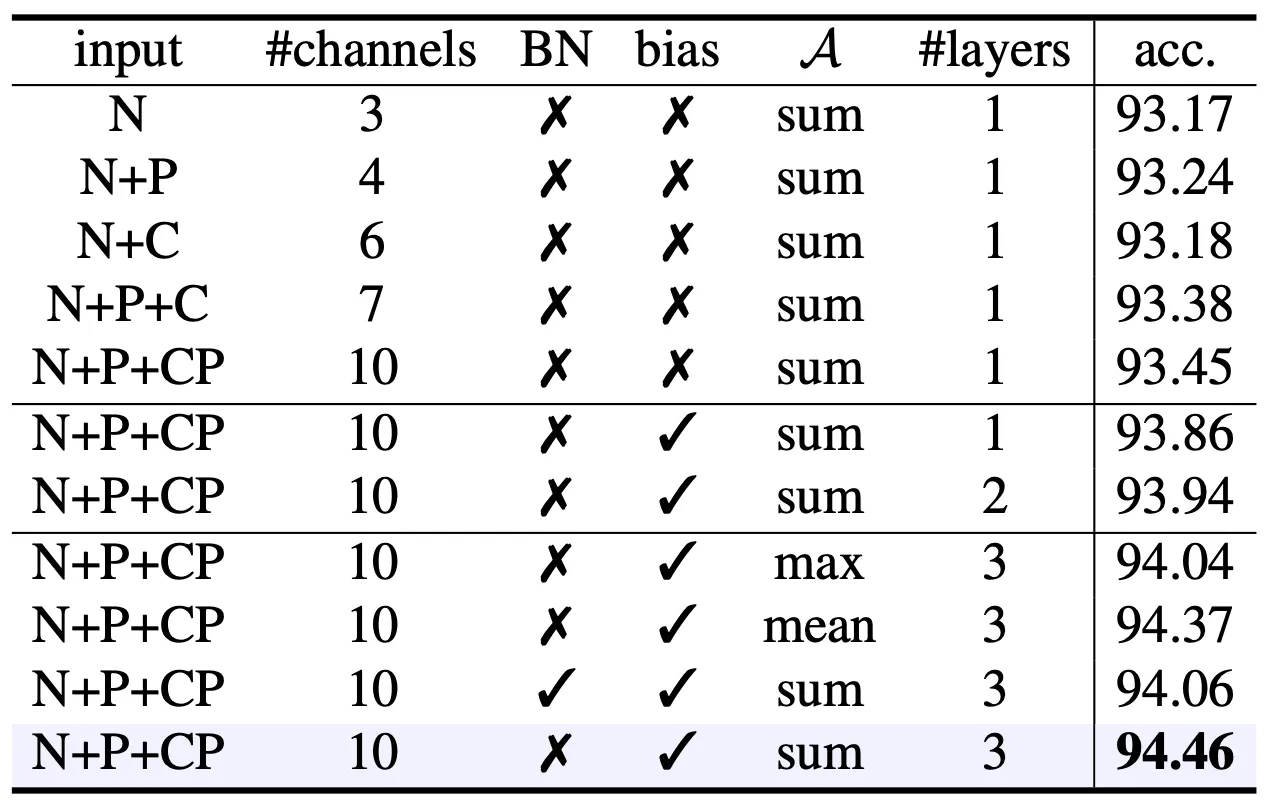
Design of RepSurf Block

구체적으로, 논문에서는 Umbrella RepSurf 를 구성하는데 들어갈 수 있는 입력 요소들을 조절해가며 Ablation Study 를 진행해봅니다. 이 뿐만 아니라 같은 입력이더라도 Tranformation function 으로 사용한 MLP 인 T\mathcal{T} 와 K 개의 삼각형들에 대한 로컬 정보를 로컬 영역으로 확장할 때 사용한 aggregation function A\mathcal{A} 를 조절하여 실험을 진행해봅니다.
Ablation Study on the Design of Umbrella RepSurf Block
위 표의 NN 은 Normal Vector, PP 는 Surface Poistion, CC 는 Centroid Position, CPCP 는 Centroid Position with Polar Auxiliary 입니다.
먼저 입력으로는 주어진 NN, PP, CPCP 를 활용한 경우가 가장 좋은 결과를 보여주었으며 첫 번째 layer 에 Batch Norm 을 사용하지 않고 bias 를 사용하며 aggregation 으로는 summation 을 사용하여 최종적으로 3 개의 layer 를 사용한 구성이 가장 좋은 accuracy 를 보여주었습니다.

Group Size

다음으로 논문에서는 Umbrella RepSurf 에서 사용할 최근접 점의 개수를 정확도와 속도 측면에서 고찰합니다.
먼저 k∈[2,12]k \in [2, 12] 일 때는 속도에 큰 차이를 보이지 않는 것을 알 수 있었습니다. 일반적으로 kk 값이 커짐에 따라서 정확도가 늘어나지만 시간도 따라서 늘어나는 것에 기반하면 k=8k=8 이 최적의 선택임을 알 수 있었다고 합니다. 더불어 kk 값이 굉장히 커지면 gradient vanishing 문제가 발생하여 더욱 좋지 못한 결과가 나옴을 확인했다고 합니다.

Polar Auxiliary

다음으로 논문에서는 Polar Auxiliary 에 대한 Ablation Study 결과를 보여줍니다.
Polar Auxiliary 를 전혀 사용하지 않았을 때의 accuracy 는 93.97% 인데 Polar Auxiliary 로 추가되는 항목 중 ρ\rho 만 추가해도 성능이 0.15% 정도 오르는 것을 확인할 수 있었다고 합니다. 이는 개인적으로 Centroid 와 근접 점 사이의 거리 정보를 명시적으로 주는 것이 도움이 되었다는 관점으로 바라볼 수 있을 것 같습니다. 최종적으로 θ\theta 와 ϕ\phi 까지 추가했을 때는 0.49% 까지 오르는 것을 확인할 수 있었습니다. θ\theta 까지만 추가한 버전으로 보이는 cylinder 의 경우는 큰 하락이 아니기 때문에 논문에서 크게 언급하지 않은 것으로 보입니다.

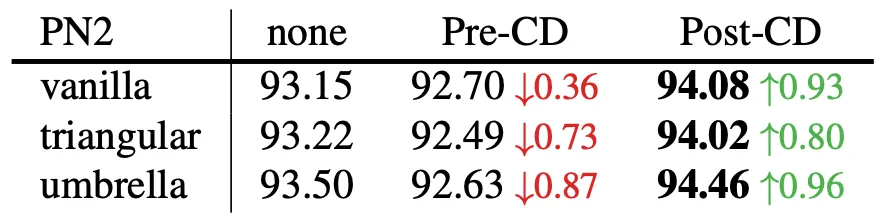
Channel Dedifferentiation

마지막으로 논문에서는 Channel Dediffernetiation 방법론으로 Pre-CD 와 Post-CD 를 비교합니다. 앞서 언급한 것처럼 Post-CD 는 linear function 을 거친 이후에 Batch Normalization 을 진행하는 것이고 Pre-CD 는 그 순서가 바뀐 것입니다.
그 결과 논문의 설계대로 Post-CD 에서 더 좋은 accuracy 를 얻음을 확인할 수 있었는데, 논문에서는 이를 입력 직후 진행하는 Batch Normalization 이 기존의 의미를 더 크게 blurring 한다는 시각으로 바라보고 있습니다.

Conclusion

이것으로 논문 “Surface Representation for Point Clouds” 의 내용을 간단하게 요약해보았습니다.
최신 CVPR 의 3D Vision 분야의 논문들을 살펴보다가 Point Cloud 에서 Surface 를 표현해낸다는 논문의 제목에 이끌려 읽어보게 된 것 같습니다. 실제로 논문의 제목처럼 Point Cloud 에서 Surface 를 Explicit 하게 만들어내고, 이것을 학습의 입력으로 함께 넣어주는 것이 실제 학습 과정에 도움이 된다- 라는 내용이었던 것 같습니다.
전체적인 방법론 자체는 Taylor Series 에 영감을 얻은 로컬 영역 구조의 표현 방법에 기반했고, 로컬 영역 구조 정보에 포함되는 개념들이 신선하거나 어렵지는 않았지만 로컬 영역의 정보라는 개념을 Normal Vector 등의 요소를 사용해 Explicit 한 벡터 형태로 정의하는 아이디어 자체는 신기했던 것 같습니다.