Duplicate

Lecture 11 | Two View Geometry I

수강 일자
2023/03/01

Epipolar Geometry

•
두 개의 view 에 대한 Projective Geometry 를 연구하는 분야.
◦
3D Structure 나 Scene 이 아니라, 두 Camera Pose 에 관한 것임.
•
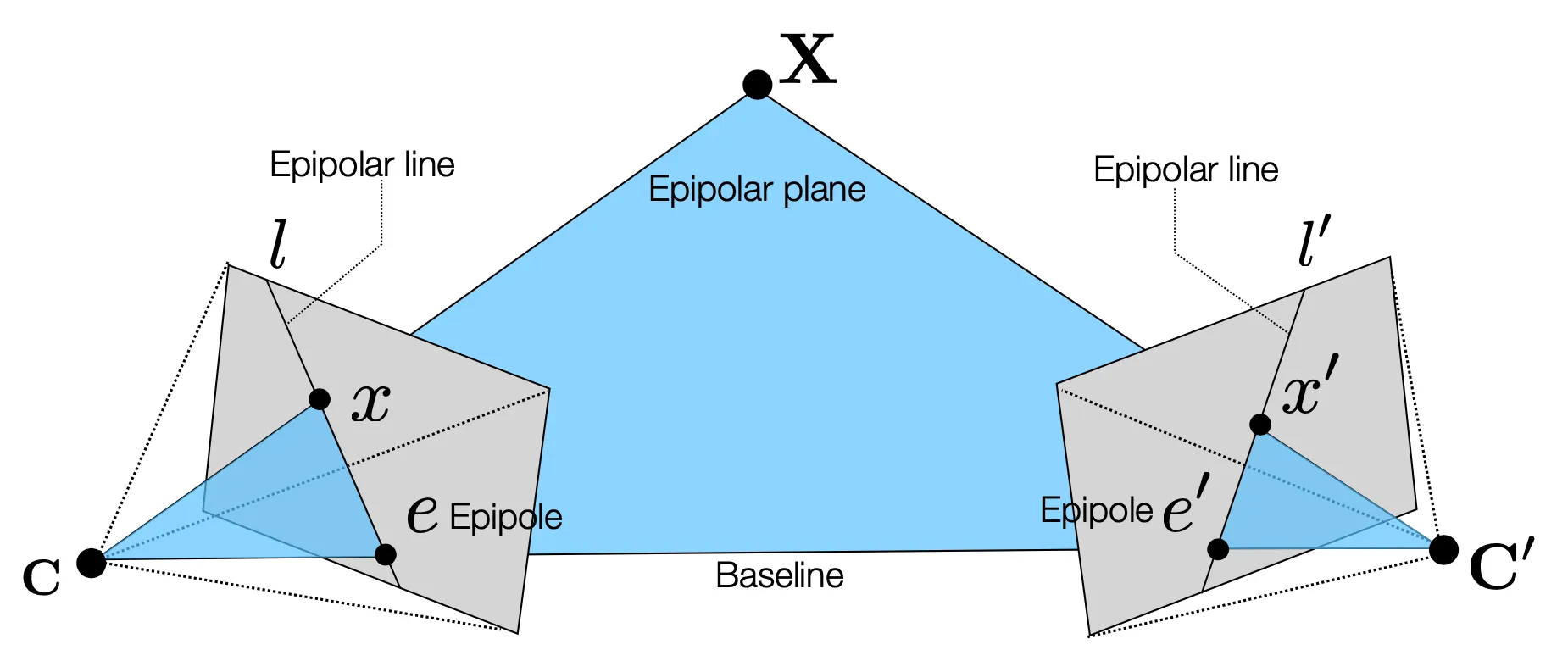
Epipolar Geometry 의 각 요소에 대한 설명 ?
◦
xx: 3D 의 한 점 X{\rm X} 가 Camera Center CC 에 대해 Image Plane ll 위에 projection 된 점
◦
x′x': 3D 의 한 점 X{\rm X} 가 Camera Center C′C' 에 대해 Image Plane l′l' 위에 projection 된 점
◦
Baseline: 두 Camera Center 를 잇는 선
◦
Epipole e,e′e, e': Baseline 과 Image Plane 의 교점
◦
Epipolar Plane: X,C,C′\rm X,C,C' 이 동시에 놓여있는 평면
▪
세 점 X,C,C′\rm X,C,C' 을 지나는 평면을 먼저 정의하면, 각 점 x,x′,e,e′x, x', e, e' 은 그 평면 위에 놓인 선 위에 존재하는 점이기 때문에 해당 평면 위에 있음
◦
Epipolar Line: Epipolar Plane 과 각 Image Plane 의 교선, (혹은 Back-Projected Ray 의 다른 Image Plane 에 대한 projection)
▪
Epipole 은 Epipolar Plane 위의 점 C,C′\rm C, C' 에 대한 projection 으로 볼 수 있기 때문에 Epipolar Line 은 항상 Epipole 을 포함함.

Properties of Epipolar Lines

•
Original 3D point X{\rm X} 가 변해도 Baseline 은 변하지 않음.
◦
Baseline 은 Camera Center 를 잇는 선이기 때문에 Camera Center 가 동일하면 변하지 않음.
•
Original 3D point X{\rm X} 의 각 Image Plane 으로의 projection 은 항상 Epipolar Line 위에 있음.
◦
Epipolar Line 은 Back-Projected Ray 의 다른 Image Plane 위로의 projection 이고, X{\rm X} 는 Back-Projected Ray 위에 있기 떄문임.
◦
이것은 두 이미지 상의 Corresponding Point 가 서로의 Epipolar Line 위에 있다는 것을 뜻하며, Corresponding Point 를 찾는데 좋은 constraint 로 사용될 수 있는 중요한 특성임.
•
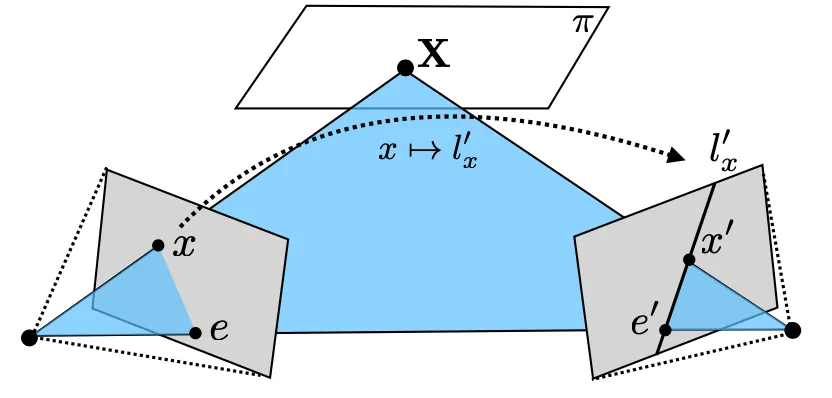
Original 3D point X{\rm X} 의 변화에 따라서 Epipolar Plane 은 Baseline 을 중심으로 회전함.
◦
Epipolar Plane 은 항상 Baseline 을 포함하고 있기 때문임.
•
Original 3D point X{\rm X} 의 변화에도 불구하고 Epipolar Line 은 항상 동일한 Epipole 을 지남. → X{\rm X} 가 바뀜에 따라서 나타날 수 있는 여러 Epipolar Line 의 교점으로 볼 수 있음.
◦
Original 3D point X{\rm X} 가 변해도 Baseline 은 변하지 않기 때문임.

Fundamental Matrix F\rm F

lx′=Fxlx=FTxl_x' = {\rm F}x \quad l_x = {\rm F}^Tx
•
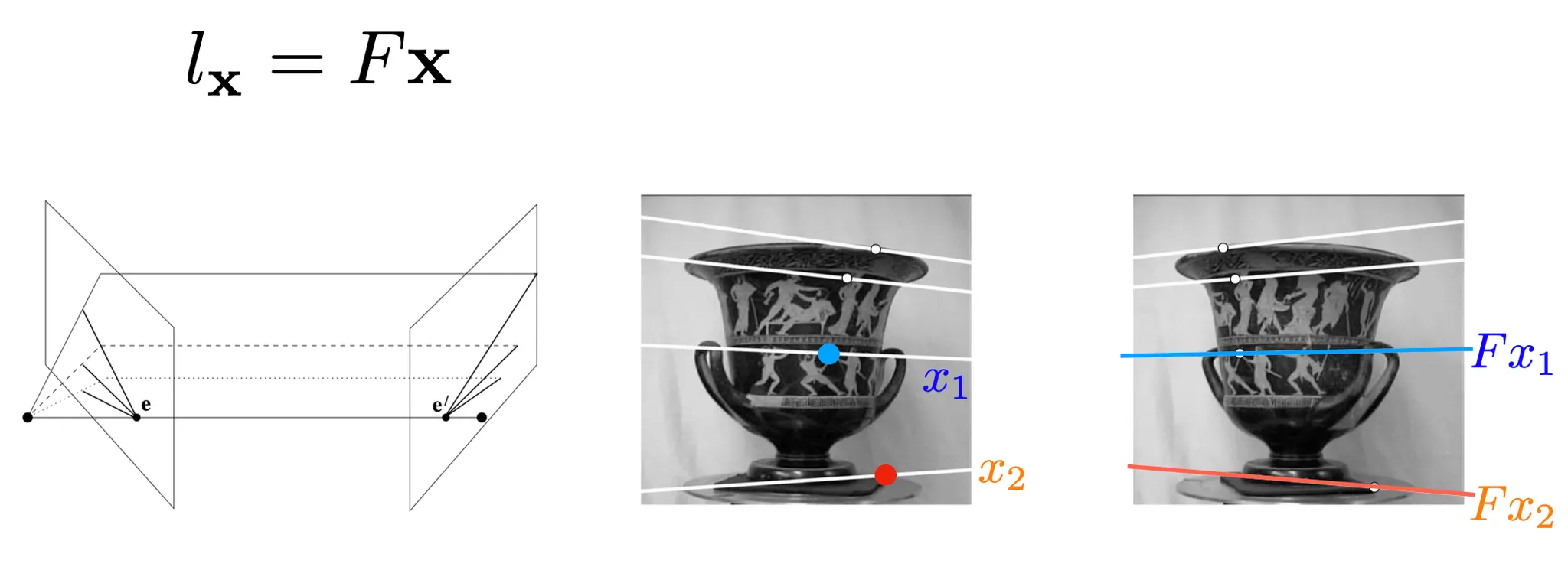
Epipolar Geometry 에서 한 이미지 위의 점에서 다른 이미지 위의 Epipolar Line 으로 대응하는 3×33\times 3 Rank 2 Mat rix 가 존재함.
•
x′x' 은 lx′l_x' 위에, xx 는 lxl_x 위에 있기 때문에 다음이 성립함.
lx′Tx′=(Fx)Tx′=xTFTx′=0x′TFx=0 (∵in the same way)l_x'^Tx' =({\rm F}x)^Tx' = x^T{\rm F}^Tx' = 0 \\ {x'^T}{\rm F}x = 0\ (\because {\rm in\ the\ same\ way})

Geometric Derivation of Fundamental Matrix F{\rm F}

•
X{\rm X} 를 지나는 plane 하나를 생각하면 Camera Center 를 공유하는 두 Plane 에 대한 Transformation 두 개를 생각할 수 있고 이 둘은 모두 Homography 이며 결론적으로 x→x′x \to x' 을 두 번의 Homography 연산이자, 또 다른 Homography 로 생각할 수 있음.
x′=Hπxx' = H_{\pi}x
•
Epipolar Line 은 Epipole 과 Corresponding Point 를 지나는 직선이므로 다음과 같은 식을 세울 수 있음.
lx′=e′×x′=[e′]×x′=[e′]×Hπx=Fxl_x' = e' \times x' = [e']_{\times}x' = [e']_{\times}H_{\pi}x = {\rm F}x
◦
[e′]×[e']_{\times } 은 3×33\times3 Skew Symmetric Matrix 이고, HπH_{\pi} 는 3×33\times3 Homography 이기 때문에 F{\rm F} 도 3×33\times 3 Matrix 가 됨.
◦
[e′]×=[0ϵ3ϵ2ϵ30−ϵ1−ϵ2ϵ10][e']_{\times} = \begin{bmatrix} 0 & \epsilon_3 & \epsilon_2 \\ \epsilon_3 & 0 & -\epsilon_1\\ -\epsilon_2& \epsilon_1 & 0\\ \end{bmatrix}이기 때문에 Rank 2 이고 Homography 는 Rank 3 (Invertible) 이기 때문에 이들의 Multiplication 인 F{\rm F} 는 Rank 2 가 됨.
◦
F{\rm F} 는 9 개의 variable 이 존재하지만 (9DoF) Up-to-Scale (-1DoF) 이고 det(F)=0det({\rm F}) = 0 의 constraint 가 존재하여 (-1DoF) 최종적으로 7DoF 임.

Geometric Meaning oF Rank 2 of F{\rm F}

•
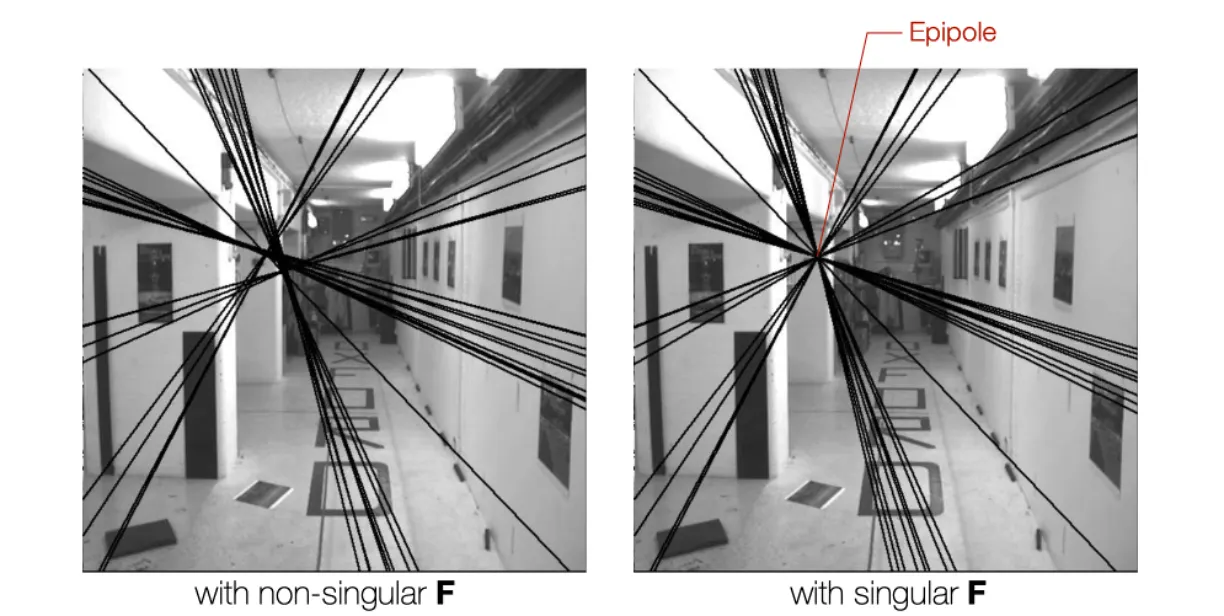
Full Rank 인 F{\rm F} 가 계산되어 사용하면 Epopolar Line 이 하나의 교점을 가지지 않음.
•
lx′=Fxl_x' = {\rm F}x 에서 point xx 는 2DoF 이기 때문에 F{\rm F} 가 Full Rank 이면 lx′{l_x'} 도 2DoF 가 되어버림. 위 그림으로 예시를 들면, 선의 yy 절편과 기울기 모두에 자유도가 있는 좌측의 그림임. 즉 F{\rm F} 는 Full Rank 일 수 없음.
•
Epipolar Line 위의 다른 점 yy 에 대해서 yy 에 대응되는 다른 Image Plane 의 Epipolar Line 또한 xx 에 대응되는 Epipolar Line 과 동일해야 함. 이 때 F{\rm F} 가 invertible 하면 1-1 mapping 만 되기 때문에 F{\rm F} 는 Non-Invertible 하고 Full Rank 일 수 없음.

Algebraic Derivation of Fundamental Matrix F{\rm F}

•
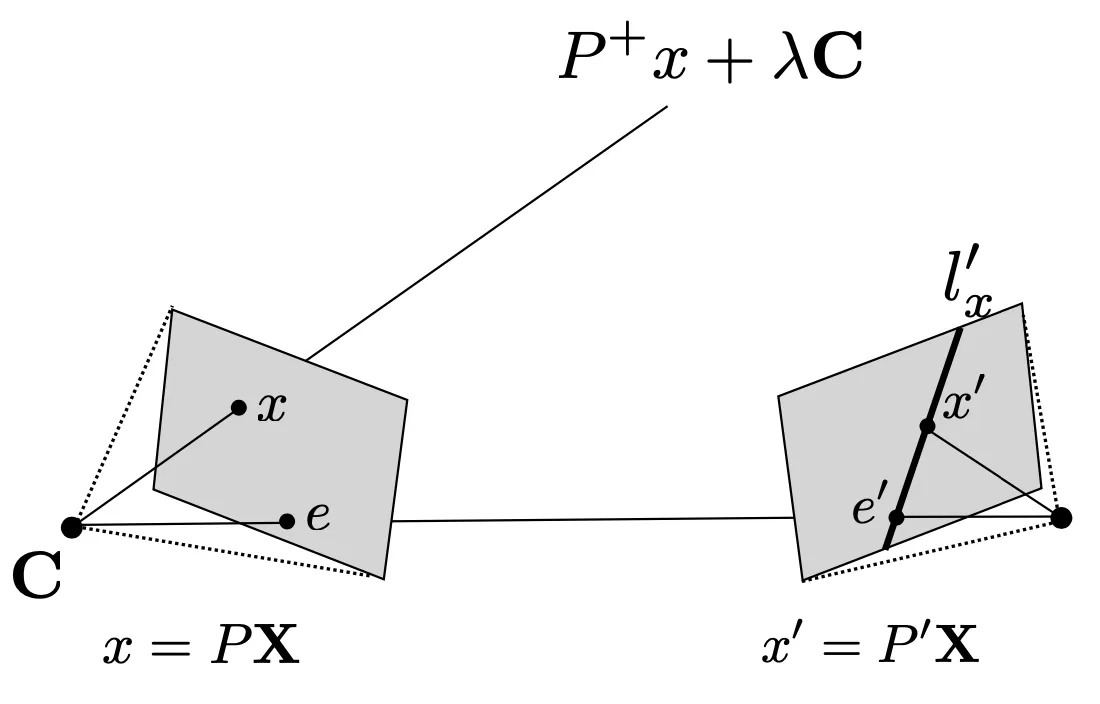
Camera Center C{\rm C} 와 Image Plane 위의 점 xx 에 대한 Back-Projected Ray 위의 점은 다음과 같이 표현할 수 있음.
P+x+λCP^+x + \lambda{\rm C}
◦
PP 는 Camera Center C{\rm C} 와 Image Plane 에 대한 projection 이고, P+P^{+} 는 PP 에 대한 pseudo-inverse 임.
•
C{\rm C} 와 λ=0\lambda=0 일 때의 Ray 위의 점인 P+xP^+ x 의 다른 Image Plane 에 대한 projection 은 모두 그 Epipolar Line 위에 있고 다음과 같이 표현할 수 있음.
lx′=P′C×P′P+x=e′×P′P+x=[e′]×P′P+xF=[e′]×P′P+l_x' = P'{\rm C} \times P'P^+x = e' \times P'P^+x = [e']_{\times}P'P^+ x \\ {\rm F} = [e']_{\times}P'P^+
◦
P′P' 은 Camera Center C′{\rm C'} 과 다른 Image Plane 에 대한 projection 임.

Fundamental Matrix F{\rm F}

•
일반성을 잃지 않고 한 Camera 의 Center 를 원점으로, Rotation Matrix 를 II 로 생각할 수 있음.
C=(01)P=K[I∣0]P′=K′[R∣t]{\rm C} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ P = K[I|0] \quad P'=K'[R|{\rm t}]
◦
이렇게 가정하면, PP 의 pseudo inversere 는 P+=[K−10T]P^+ = \begin{bmatrix} K^{-1} \\ 0^T \end{bmatrix} 가 됨.
◦
Epipole 들은 각 Camera Center 를 서로의 Image Plane 에 projection 한 점이므로 다음과 같음.
e=P(−RTt1)=KRTte′=P′(01)=K′te = P \begin{pmatrix} -R^T{\rm t}\\ 1 \end{pmatrix} = KR^T{\rm t} \\ e' = P' \begin{pmatrix} 0\\ 1 \end{pmatrix} = K'{\rm t} \\
•
이러한 가정 속에서 Fundamental Matrix F{\rm F} 는 다음과 같이 표현할 수 있음.
F=[e′]×P′P+=[P′C]×P′P+=[K′t]×K′RK−1=K′−T[t]×RK−1\begin{align*} {\rm F} &= [e']_{\times}P'P^+ \\ &=[P'{\rm C}]_{\times}P'P^+ \\ &= [K'{\rm t}]_{\times}K'RK^{-1} = K'^{-T}[{\rm t}]_{\times}RK^{-1} \end{align*}
◦
마지막 변환은 다음과 같은 일반적인 관계에 의해서 성립함.
[Mx]×M=M∗[x]×[Mx]_{\times}M = M^*[x]_{\times}
▪
M∗M^* 는 Cofactor Matrix 로 MM 이 invertible 하면 M∗=det(M)M−TM^* = det(M)M^{-T} 임. 많은 경우에 MM 이 Up-to-Scale 하기 때문에 M∗=M−TM^* = M^{-T} 이기도 함.
▪
구체적으로 다루지는 않음.
◦
추가로, MM 이 Rotational Matrix 일 경우 다음이 성립하여, 최종적으로 F{\rm F} 를 변환할 수 있음.
R[RTt]=[t]××R→K′−T[t]×RK−1=K′−TR[RTt]×K−1=K′−TRK−T[e]×R[R^T{\rm t}] = [{\rm t}]_{\times} \times R \\ \to K'^{-T}[{\rm t}]_{\times}RK^{-1} = K'^{-T}R[R^T{\rm t}]_{\times}K^{-1} =K'^{-T}RK^{-T}[e]_{\times}
▪
마찬가지로, 구체적으로 다루지는 않음.
•
결국 F,e,e′{\rm F}, e,e' 을 K,K′,R,tK,K',R,{\rm t} 만을 사용하여 표현할 수 있음!

Fundametal Matrix F{\rm F}: Summary

x′TFx=0xTFTx′=0{x'}^T{\rm F}x = 0 \quad x^T{\rm F}^Tx' = 0
•
F{\rm F} 는 Rank 2 Homogeneous Matrix (7DoF)
•
Epipolar Lines: lx′=Fx,lx=FTx′l'_x = {\rm F}x, l_{x} = F^Tx'
•
Epipole 에 대응되는 Epipolar Line: Fe=0,FTe′=0{\rm F}e = 0, {\rm F}^Te' = 0
◦
모든 Epipolar Line 은 Epipole 을 지나기 때문에 모든 xx 에 대해 e′T(Fx)=(e′TF)x=0e'^T({\rm F}x) = (e'^T{\rm F}) x = 0 이고, e′TF=0e'^T{\rm F} = 0 임을 알 수 있음.

Epipolar Constraints for Corresponding Points

•
특정 점과 대응되는 다른 이미지 위의 점은 해당 점에서 다른 이미지의 Epipolar Line 을 계산하여 그 Epipolar Line 위에 있음. → 이를 Epipolar Constraint 라고 함.
•
즉, 특정 점의 Corresponding Point 를 찾기 위해서는 Epipolar Line 을 찾고 그 위에서만 찾으면 됨.

Pure Translation

•
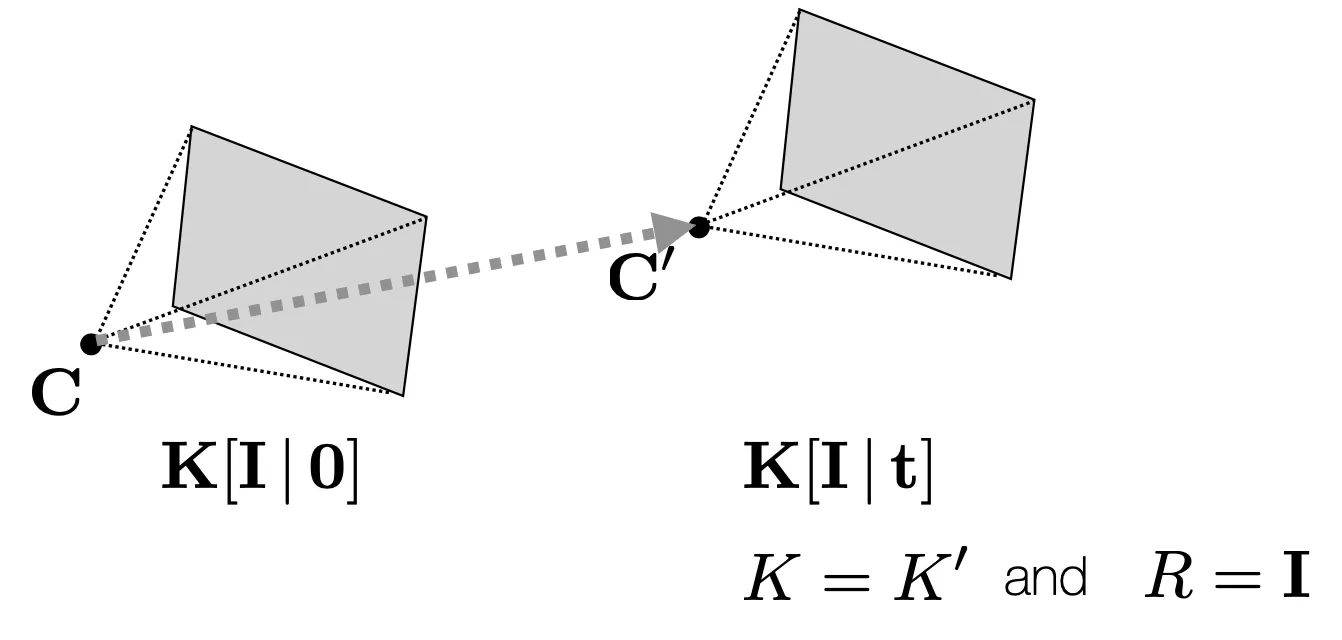
두 Camera Center 사이에 Pure Translation 만 있는 경우는 일반성을 잃지 않고 다음과 같은 상황을 고려할 수 있음.
P=K[I∣0]P′=K[I∣t]K=K′R=IP = K[I|0] \quad P' = K[I|{\rm t}]\\ K=K' \quad R=I
•
이러한 경우에는 특별하게 F{\rm F} 가 계산될 수 있음.
F=[e′]×K′RK−1=[e′]×KK−1=[e′]×{\rm F} =[e']_{\times}K'RK^{-1} = [e']_\times KK^{-1}= [e']_{\times}
•
X-Axis 에 평행하게 Camera 를 움직인 경우는 다음과 같이 특별하게 계산할 수 있음.
t=[t100]→e′=P′(001)=K′t≡(100){\rm t} = \begin{bmatrix} t_1 \\ 0 \\ 0 \end{bmatrix} \to e' = P' \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = K'{\rm t} \equiv \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}
◦
KK 는 Upper Triangluar Matrix 임을 잊지 말자!
◦
F=[e′]{\rm F=[e']} 이기 때문에 다음과 같이 표현할 수 있음.
F=[00000−1010]{\rm F} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \\ \end{bmatrix}
◦
x′TFx=0x'^T{\rm F}x = 0 의 constraint 는 다음과 같이 변형됨.
[x′y′1][00000−1010][xy1]=0→y=y′\begin{bmatrix} x' & y' & 1 \end{bmatrix} \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = 0 \to y=y'
▪
동일한 yy 축 위의 점에 Corresponding Point 가 존재함. → Stereo Matching Problem