Lecture 14 | Classification

형태
Machine Learning
수강 일자
2022/10/19

Binary Linear Classification

•
Input: x=(x1,...,xN)T{\rm x} = (x_1,...,x_N)^T, xi∈RDx_i \in \mathbb{R}^D
•
Target: t=(t1,...,tN)T{\rm t} = (t_1,...,t_N)^T, ti∈{0,1}t_i \in \{ 0, 1\}
◦
사실 {0,1}\{ 0, 1\} 말고 다른 것을 써도 되긴 하는데 (ex. {−1,+1}\{ -1 ,+1\}) 보통 이렇게 많이 설계함
•
z=wTx+bz = {\rm w^Tx} + b 로 model 을 설계하고, w{\rm w} 와 bb 를 learnable weight 로 설정함
•
prediction y={1  if z≥r0  if z<ry = \begin{cases} 1 \thickspace {\rm if}\ z \ge r \\ 0 \thickspace {\rm if}\ z < r \end{cases}
◦
WLOG, r=0r=0 으로 설정할 수 있음
•
결국 Binary Linear Classification 문제는 다음과 같이 정의됨
intermediate value z=wTxprediction y={1  if z≥00  if z<0{\rm intermediate\ value\ }z = {\rm w^T x} \\ {\rm prediction}\ y = \begin{cases} 1 \thickspace {\rm if}\ z \ge 0 \\ 0 \thickspace {\rm if}\ z < 0 \end{cases}

How to define Loss Functions for Classification

•
First Attemp: 0-1 Loss
L0−1(y,t)={0  if y=t1  if z≠t=I[y≠t]{\mathcal L_{0-1}}(y,t) = \begin{cases} 0 \thickspace {\rm if}\ y =t \\ 1 \thickspace {\rm if}\ z \ne t \end{cases} =\mathbb I[y\ne t]
◦
맞으면 loss 가 0, 틀리면 loss 가 1
◦
Averaged Loss
J=1N∑i=1NI[y(i)≠t(i)]{\mathcal J} = \frac{1}{N}\sum_{i=1}^N {\mathcal I}[y^{(i)}\ne t^{(i)}]
◦
Limitation
동일한 판단을 하는 모든 결정경계가 동일한 loss 를 가지기 때문에 거의 모든 영역에서 gradients 가 0 이고 w\rm w 를 optimize 할 수 없음!
•
Second Attemp: Squared Error Loss (from Linear Regression)
LSE(y,t)=12(y−t)2{\mathcal L}_{SE}(y,t) = \frac{1}{2}(y-t)^2
◦
그냥 naive 하게 true 값과의 차이를 통해 penalize
◦
y=wTx>0y = {\rm w^T x} >0 인 경우에 true 로 예측
◦
Limitation
Decision boundary 가 데이터 x\rm x 의 크기에 영향을 받고, 극단적으로 크기가 큰 데이터가 존재함에 따라 decision boundary 가 정상적으로 잡히지 않을 수 있음!
•
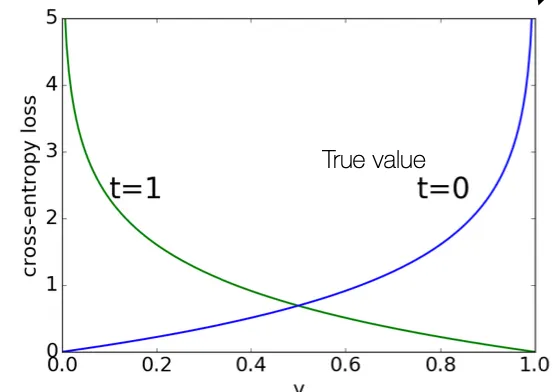
Third Attemp: (Binary) Cross Entropy
◦
Sigmoid Function
σ(x)=11+e−x\sigma(x)=\frac{1}{1+e^{-x}}
▪
산출값을 0~1 사이로 bounding 시킬 수 있음
◦
wTx\rm w^Tx 산출값에 sigmoid 를 씌워 0~1 사이로 bounding 하고, 0.5 를 기준으로 thresholding 할 수 있음! (sigmoid 에서 0.5 thresholding 은 wTx\rm w^Tx 에서 0 thresholding 과 같음)
LCE(y,t)={−log⁡y  if t=1−log⁡(1−y)  if t=0=−tlog⁡y−(1−t)log⁡(1−y){\mathcal L}_{CE}(y,t) = \begin{cases} -\log y \thickspace {\rm if}\ t=1 \\ -\log(1-y) \thickspace {\rm if}\ t=0 \end{cases} = -t\log y - (1-t)\log(1-y)
◦
y∈[0,1)y \in [0,1) 인데, t=1t=1 일 떄는 yy 가 0 에 가까울 때 크게 penalize 하고 t=0t=0 일 때는 yy 가 1 에 가까울 때 크게 penalize 함
◦
Sigmoid 이후 squared error 를 쓰는 것보다는 optimization 속도가 빠르다는 장점이 있음 (log⁡\log 값이 0 ~ 1 사이에서 절댓값이 크기 때문에…)

Recall: Cross Entropy in Kullback-Leibler (KL) Divergence

•
두 distribution p(x)p(x) 와 q(x)q(x) 의 차이를 측정할 수 있는 지표
KL(p∥q)=−∫p(x)ln⁡q(x)dx−(−∫p(x)ln⁡p(x)dx)=H(p,q)−H(p)\begin{align*} {\rm KL}(p \| q) &= -\int p(x) \ln q(x) dx - (-\int p(x) \ln p(x) dx) \\ &= H(p,q)-H(p) \end{align*}
◦
HH 항목이 cross entropy 였음
◦
구해낸 함수 q(x)q(x) 가 얼마나 p(x)p(x) 와 다른가를 측정하는 지표

Multi-class Classification

•
Logistic Regression 을 다중 categories 로 generalize 해야 함
•
산출 값이 여러 개가 될 것인데, 이들을 one-hot vector 형태로 바꾸기 위해서 maximum 을 1 로 나머지를 0 으로 바꾸는 방법이 있을 수 있음.
◦
하지만, 이 방법은 differentiable 하지 않아 optimize 할 수 없음
•
Softmax Function
Softmax(z⃗)i=ezi∑j=1Kezj{\rm Softmax}(\vec z)_i =\frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}
◦
Softmax 를 거친 벡터의 각 항목을 더하면 1 이 됨
◦
Max function 의 soften 버전이라고 보아도 됨
◦
k=2k=2 의 경우에 softmax 는 sigmoid 형태가 됨
p1(x)=exp⁡(w1Tx)exp⁡(w1Tx)+exp⁡(w2Tx)=11+exp⁡((w2−w1)Tx)=11+exp⁡(−wTx)\begin{align*} p_1(x)&=\frac{\exp(w_1^T{\rm x}) }{\exp(w_1^T{\rm x}) + \exp(w_2^T{\rm x}) } \\ &= \frac{1}{1 +\exp((w_2-w_1)^T{\rm x}) } \\ &= \frac{1}{1 +\exp(-w^T{\rm x}) } \end{align*}
•
Cross Entropy Loss
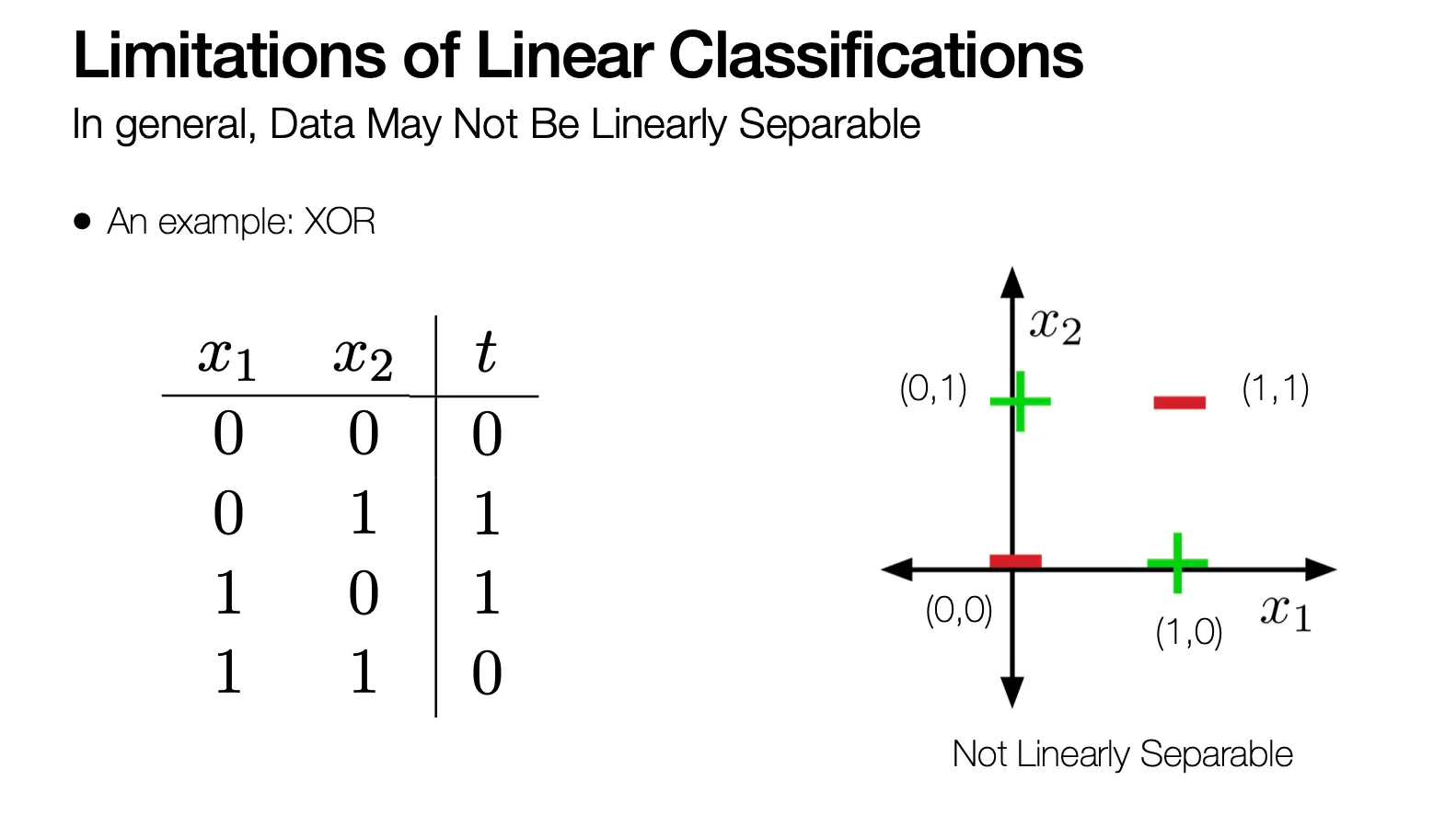
LCE=−tT(log⁡y)=−∑ktilog⁡yi{\mathcal L}_{\rm CE} = -{\rm t}^T(\log {\rm y}) = - \sum_k t_i \log y_i

Limitations of Linear Classifications

•
실제 상황에서는 데이터가 linear 하게 separable 하지 않을 수도 있음 (ex. XOR)
•
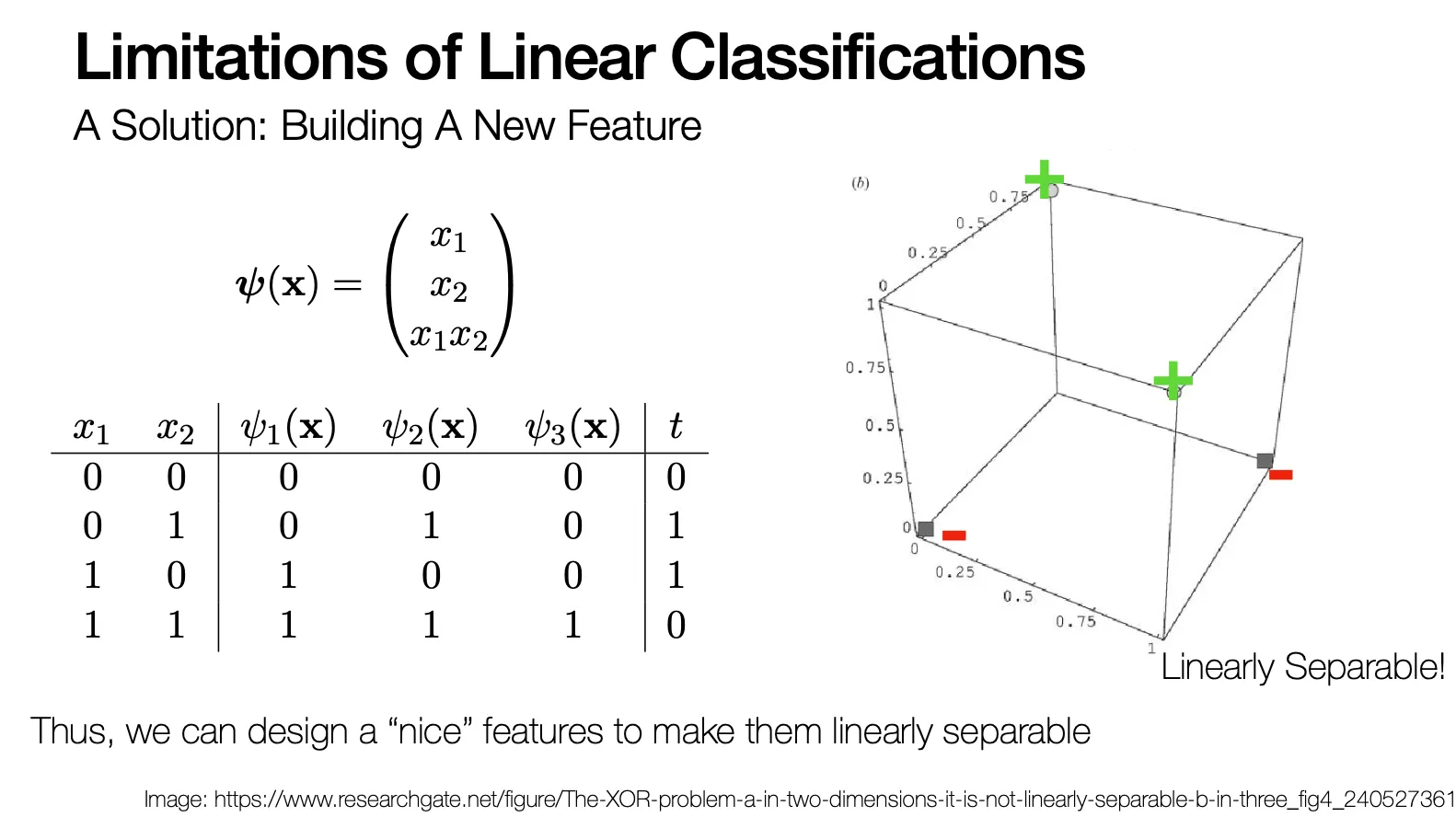
이러한 상황에서 새로운 feature 를 만드는 형태로 해결할 수 있음 (차원을 추가하여 linearly separable 하도록 만들어버림)
ψ(x)=(x1x2x1x2)\psi(x) = \begin{pmatrix} x_1 \\ x_2 \\ x_1x_2 \end{pmatrix}