A Brief History of Images
•
Camera Obscura: 최초의 카메라 (Pin Hole)
•
Lens Based Camera Obscura: 빛을 모아주는 렌즈를 활용한 카메라
•
Niepce → 최초의 사진을 만들어냄
◦
Silver Salt 가 빛을 받으면 받을수록 검은색으로 변하는 것을 통해 반전된 사진을 얻어냄.
◦
영구적인 사진은 아님. (빛이 닿는 순간 전체가 검은색으로 변하기 때문)
•
Niepce → 최초의 영구적인 사진도 만들어냄
◦
Pewter 라는 물질을 사용하고, 약 8시간동안 빛을 쪼이면 그 이후에는 변하지 않음.
•
Daguerre → 은판사진법
◦
종이에 빛의 강약을 기록하는 것이 핵심
◦
복잡한 과정을 통해서 이루어짐 (크게 다루지는 않음)
•
Henry Fox Talbot → Negative to Posiive Photographic Process
◦
하나의 negative 를 만들면 이를 이용해 사진을 원하는 수 만큼 계속 만들 수 있음.
•
James Clerk Maxwell → 최초의 컬러 사진
◦
CMU 의 상징적인 체크무늬인 Tartan ribbon 의 사진
•
Hauron → Subtractive Color Photograph
◦
빛의 삼원색 아이디어를 사용해 컬러 사진을 현실적으로, 좀 더 쉽게 찍을 수 있는 방법을 개발
•
Leland Stanford → Fast Motion using 24 Cameras
◦
24 개의 카메라를 이용해 말이 달릴 때 발이 닿는 순서를 촬영하는데 성공
◦
4 개의 발이 모두 땅에 닿아있지 않은 상태가 존재함을 보임.
•
Leica → 35 mm 형태의 휴대 가능한 카메라
•
Polaroid Coropration → 즉석사진기
•
CCD 칩의 등장
◦
필름 카메라의 단점
▪
32, 48 장밖에 못 찍음.
▪
필름, 카메라가 비쌈.
▪
현상 인화에도 시간이 오래 걸림.
◦
빛의 많고 적음이 CCD 셀에 측정이 되고 전기신호로 변환이 되며 기록이 됨.
◦
요새는 CCD 대신에 CMOS 를 활용
Let’s Design a Camera
•
Film 에 물체의 모습을 나타내는 빛을 기록하려고 할 때, 물체의 앞에 Film 을 놓는 방법을 생각할 수 있음.
◦
Film 의 한 점에 여러 지점에서 반사된 빛이 모이기 떄문에 환경에 대한 기록이 불가능함.
•
Film 과 물체 사이에 barrier 를 두고, 작은 구멍을 뚫는 방법을 생각할 수 있음.
◦
Barrier 와 그 위에 구멍을 뚫음으로써 물체의 한 지점과 Film 의 한 지점에 대한 1:1 mapping 을 지정해줄 수 있음.
◦
구멍 (Pin Hole) 을 Aperture, Center of Projection, Focal Point, Camera Center 라고도 부름.
◦
구멍을 통과하는 ray 를 Pencil of Rays 라고도 부름.
◦
이미지가 맺히는 Film 을 Image Plane 이라고도 부름.
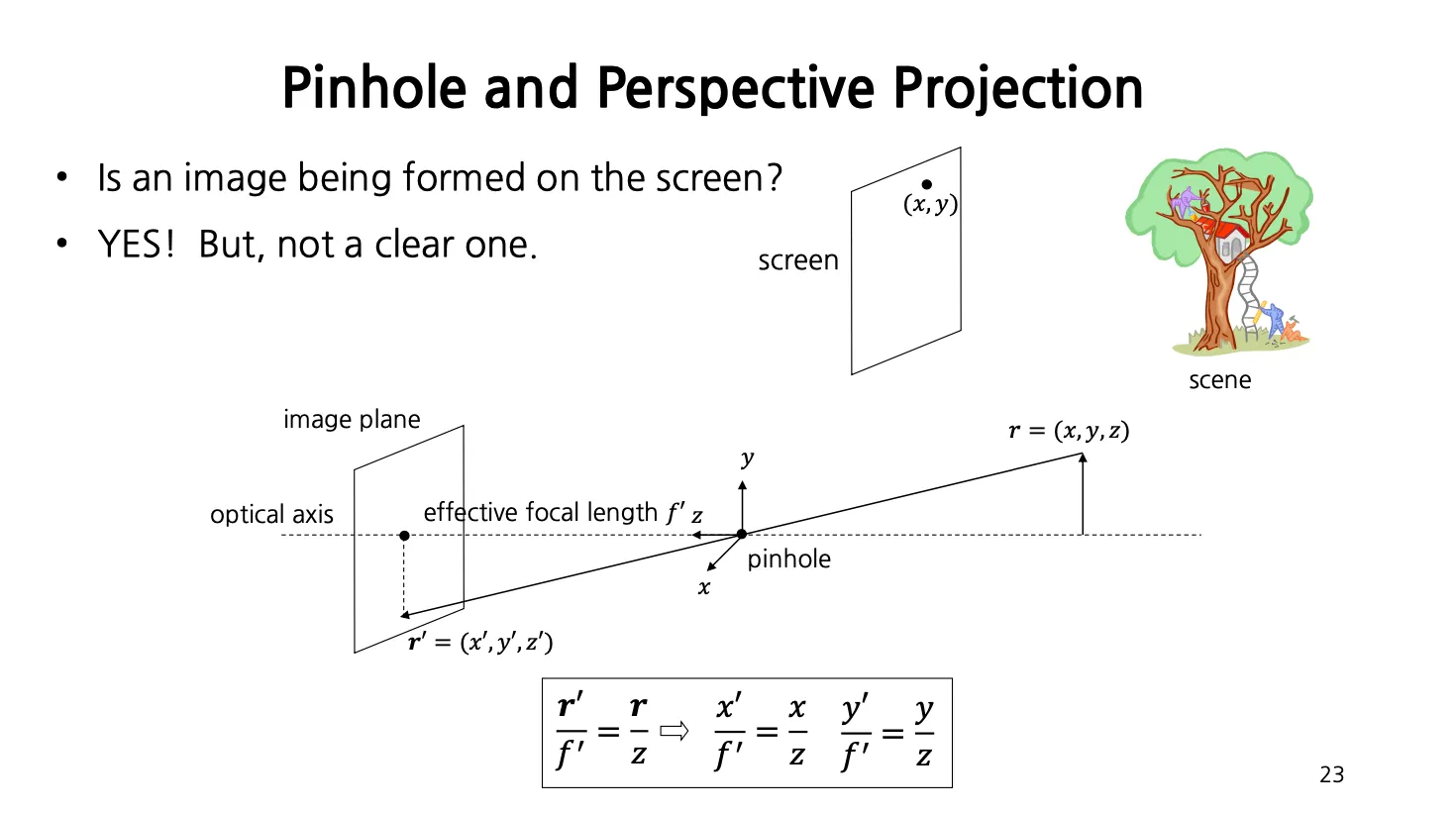
Pinhole and Perspective Projection
•
Perspective Projection: Pinhole 을 통해 3차원 공간이 Image Plane 상의 점으로 맺히는 것
•
: 물체의 한 지점
•
: 물체의 한 지점에 대응되는 Image Plane 의 한 지점
•
: Effective Focal Length, Pinhole 로부터 Image Plane 까지의 수직거리
Magnification
•
Planar Scene 의 점 에서 점 로 물체의 지점이 이동했을 때의 이동거리를 라 할때 Image Plane 에서의 맺히는 상 과 사이의 거리 과의 관계를 계산할 수 있음.
•
Magnification 은 아래와 같이 나타낼 수 있음.
•
마찬가지로, 영역에 대한 비율은 이 됨.
Problems with Pinholes
•
Pinhole 구멍이 작은 경우
◦
장면과 Image Plane 상의 1대1 대응이 명확해지기 떄문에 상이 뚜렷함.
◦
하지만, 구멍을 통과하는 빛의 양이 적어 상이 어두움
•
Pinhole 구멍이 큰 경우
◦
구멍을 통과하는 빛의 양이 많이 상이 잘 보임.
◦
상의 하나의 점이 Image Plane 의 여러 점에 관여를 하기 때문에 상이 뚜렷하지 않음. (Lower Contrast, Blurry Image)
•
선명한 이미지를 얻고 싶다면, Pinhole Size (Aperture) 를 작게 가져가야 하지만, 어두운 이미지를 얻을 수 있음.
•
하지만, 구멍을 또 너무 작게 만들면 다시 선명하지 못한 이미지를 얻는데, 이는 Diffraction 때문에 1:1 mapping 이 깨지기 때문임.
•
일반적으로 선명한 이미지를 얻기 위한 Pinhole Diameter 의 설정 공식이 있음.
◦
: Pinhole Diameter
◦
: Effective Focal Length
◦
: Wavelength of Light
Dimensionality Reduction: from 3D to 2D
•
Perspective Projection 을 통해서 보존 되는 것
◦
Straight Line (직선은 3D 에서 2D 로 매핑되어도 직선)
•
Perspective Projection 을 통해서 보존 되지 않는 것
◦
Angle, Length
Fronto-Parallel Planes
•
Image Plane 과 평행인 plane 에 대한 고려
◦
Image Plane 위의 점들은 동일한 고정된 depth 를 가짐.
◦
Pattern 은 동일하게 로 scale 됨.
◦
Plane 위의 점들이 가지는 각도, Plane 위의 점들의 실제 길이와 상 위의 길이의 비율, Plane 위의 점들이 이루는 실제 넓이와 상 위에서 해당되는 넓이의 비율이 유지됨.
Projection of a Line
•
Image Plane 을 Optical Center (Pinhole, Aperture) 앞 지점에 있다고 가정하고 그림을 그리면, 상이 뒤집히지 않아도 되게끔 그려줄 수 있기 떄문에 간혹 이러한 형태의 그림을 사용함.
•
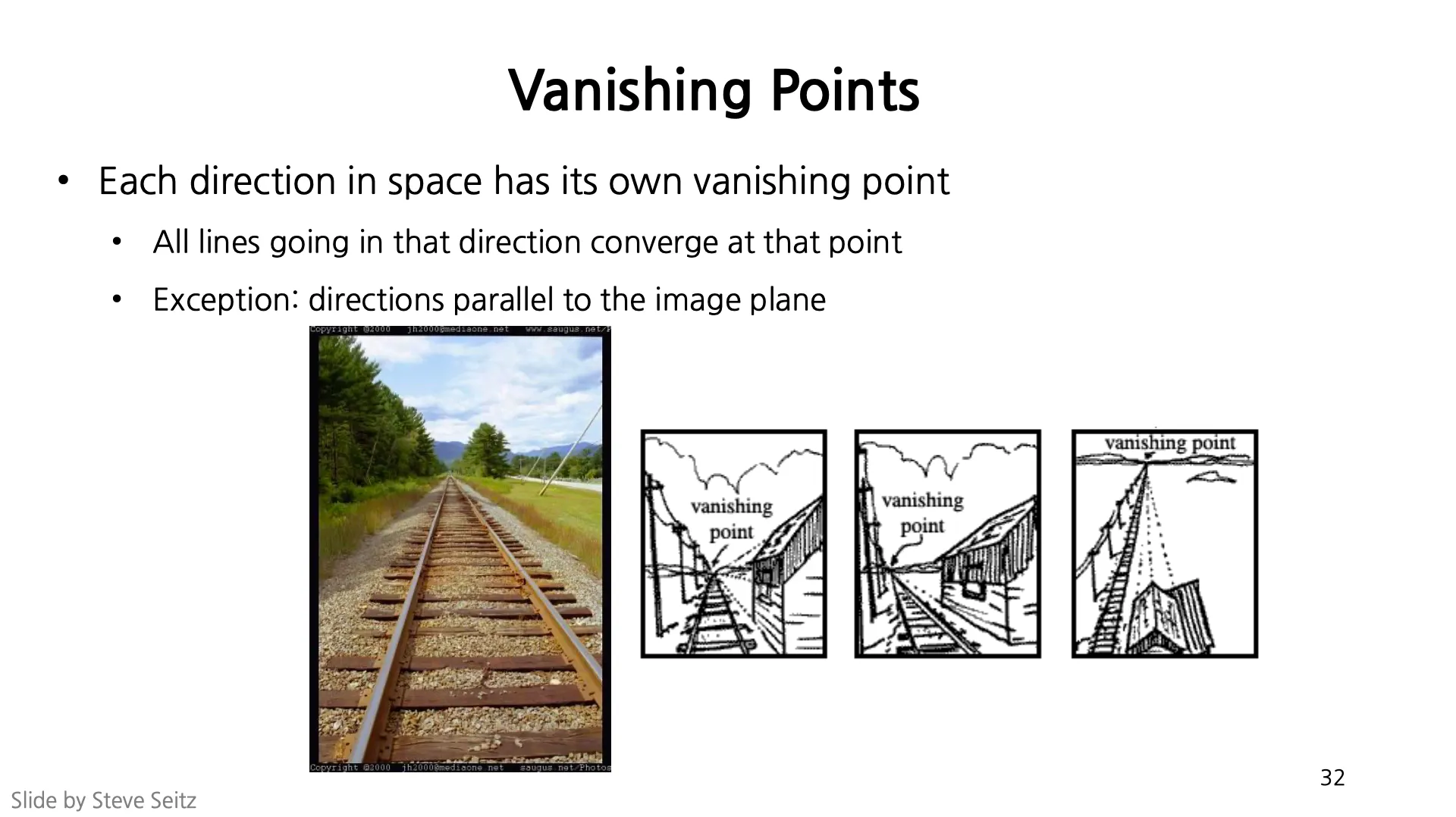
환경 상에 존재하는 직선 위의 점들을 Image Plane 에 투영하면, 선이 무한대로 멀어지는 점에서 Vanishing Point 로 이동하며, 그와 평행인 모든 선들은 같은 Vanishing Point 를 가짐.
•
Ground Plane 위의 모든 선들에 대응되는 Vanishing Point 의 집합은 선 형태를 이루는데, 이를 Horizon (지평선) 이라고 함.
◦
Horizon 선은 카메라의 height 를 나타내고, 이미지 상에서 Horizon 위에 있는 점들은 카메라보다 절대적인 height 가 높고, Horizon 아래에 있는 점들은 카메라보다 height 가 낮음.
Perspective Cues
•
똑같은 키를 가진 사람은 이미지 상에서 멀리 있는 친구가 작게 표현되어야 자연스러움.
•
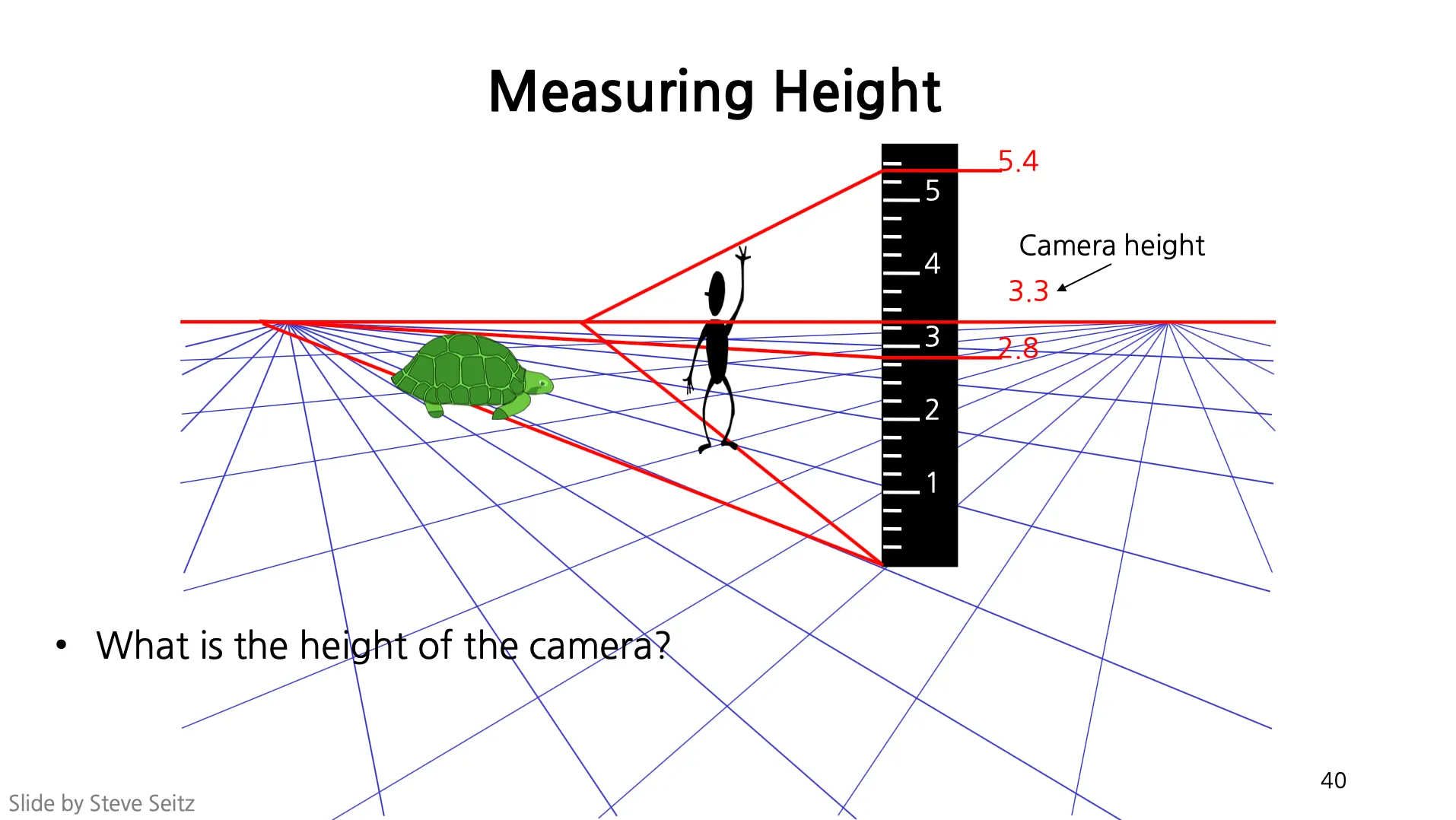
환경 상에 자를 두고 사진을 찍으면 실제 키를 알 수 있음.
◦
자의 밑바닥과 사람의 밑바닥을 연결하고 지평선과 만나는 점을 찾음.
◦
지평선과 만나는 점과 사람의 위를 연결하고 자와 만나는 점을 찾음.
◦
자의 밑바닥과 자와 만나는 점 사이의 거리가 실제 키가 됨.
Perspective in Art
•
피렌체의 성당 그림은 Perspective Projection 에 대한 일관성을 유지하면서 그린 그림임.
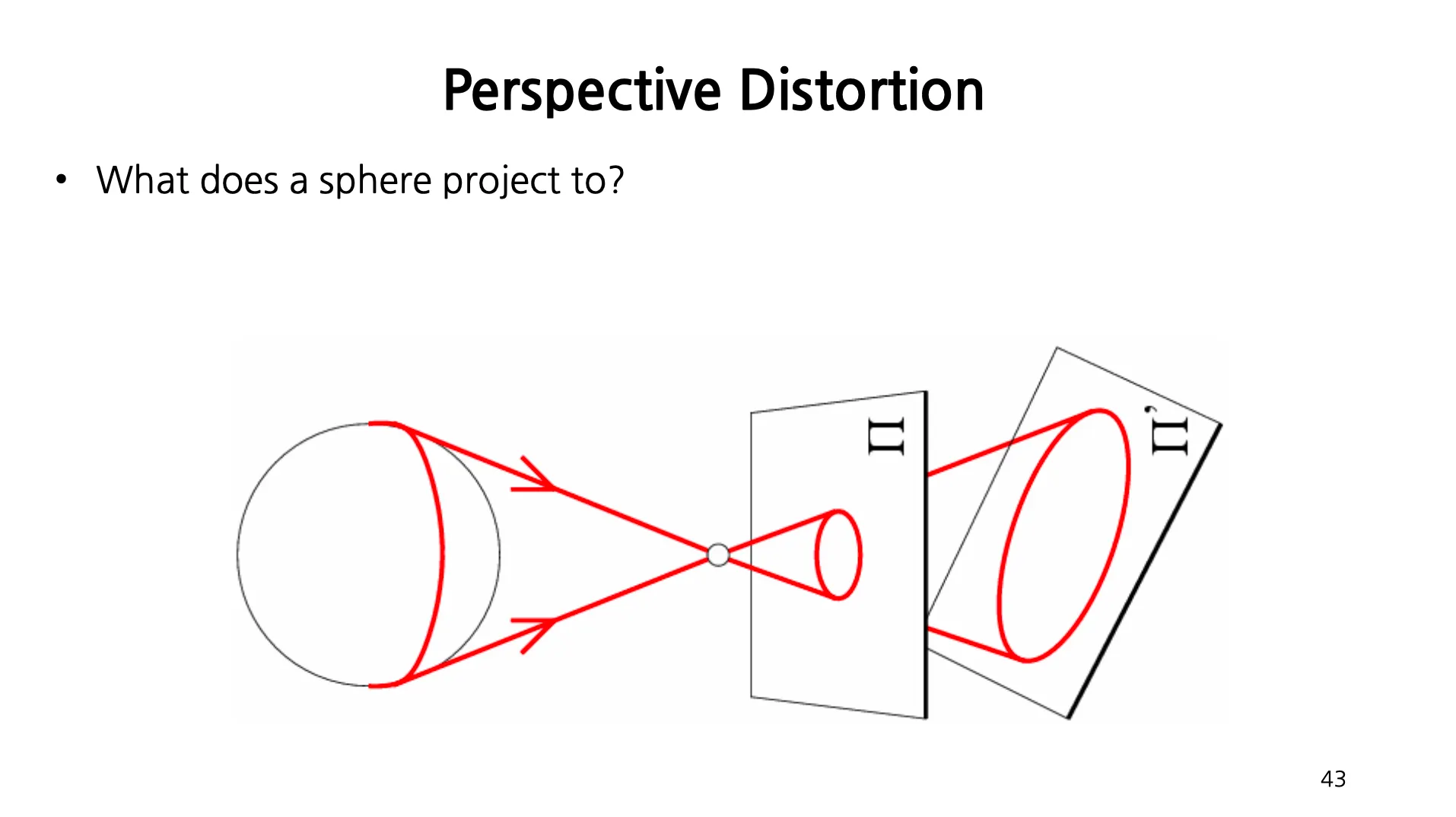
Perspective Distortion
•
구형 물체가 Image Plane 의 각도에 따라서 타원체로 보임.
•
등간격, 등크기 물체가 Pinhole 의 위치에 따라서 크기와 간격이 다르게 보임.