Image Matching - Not Always Easy
•
화성탐사로봇이 연속적으로 촬영한 사진은 지구에서 매우 멀리 떨어진 곳에서 고화질의 사진을 전송하려다 보니, 연속된 두 사진이라도 매우 큰 time difference 를 가짐.
•
매우 큰 time difference 를 가진 두 사진에서 겹치는 부분을 찾는 것은 사람에게도 어려운 일임.
•
하지만 SIFT Feature 를 뽑아서 비교해보면 겹치는 부분을 찾기 어려웠던 두 사진 속에서도 겹치는 부분을 찾을 수 있음.
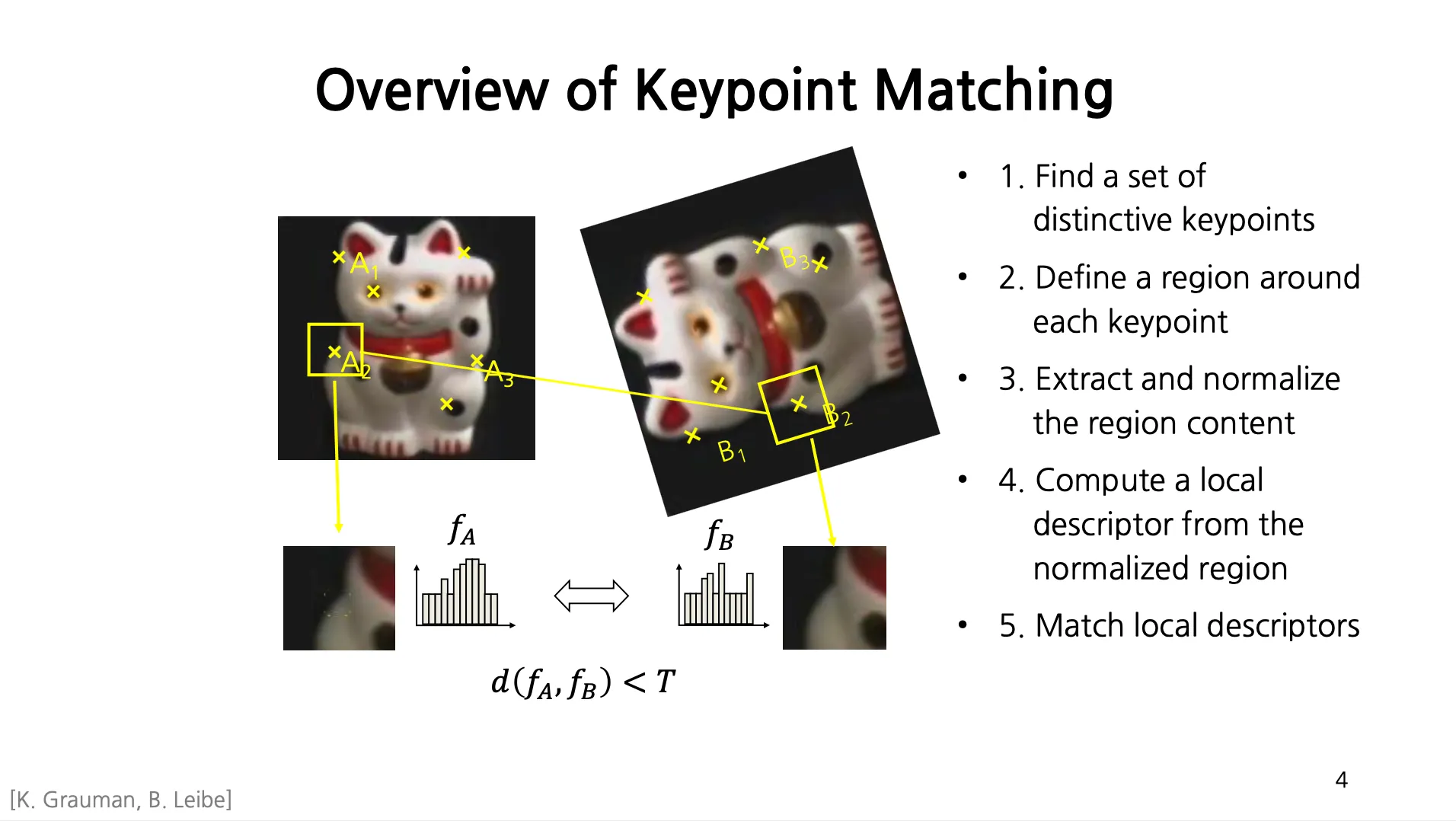
Overview of Keypoint Matching
1.
특색이 있는 distinct keypoints 세트를 찾음.
a.
좋은 keypoints 세트는 repeatable 하고 distinct 함.
b.
Repeatability: 동일한 feature 가 두 개 이상의 이미지에서 보여야 함.
c.
Distinctiveness: 다른 feature 는 다르게 보여야 함. (귀 끝과 코 끝을 keypoints 로 잡았다고 할 때, 이 둘이 비슷해보이면 안됨!)
d.
다양한 keypoints detector 가 발전해 왔음. → Online 에서 체험해볼 수 있음.
e.
사진이나 비디오를 볼 때 우리가 집중해서 보는 fixation points 가 있고, 이를 옮겨가는 과정인 saccade 가 존재함.
2.
찾은 keypoints 주변 영역을 설정함.
3.
주변 영역의 컨텐츠를 추출하고 normalize (direction, scale 을 맞춰줌) 함.
4.
추출한 영역으로부터 (Histogram 형태의) Local Descriptor 를 계산함.
5.
Local Descriptor 사이의 거리가 특정 threshold 보다 작으면 Matching 되었다고 결론을 내림.
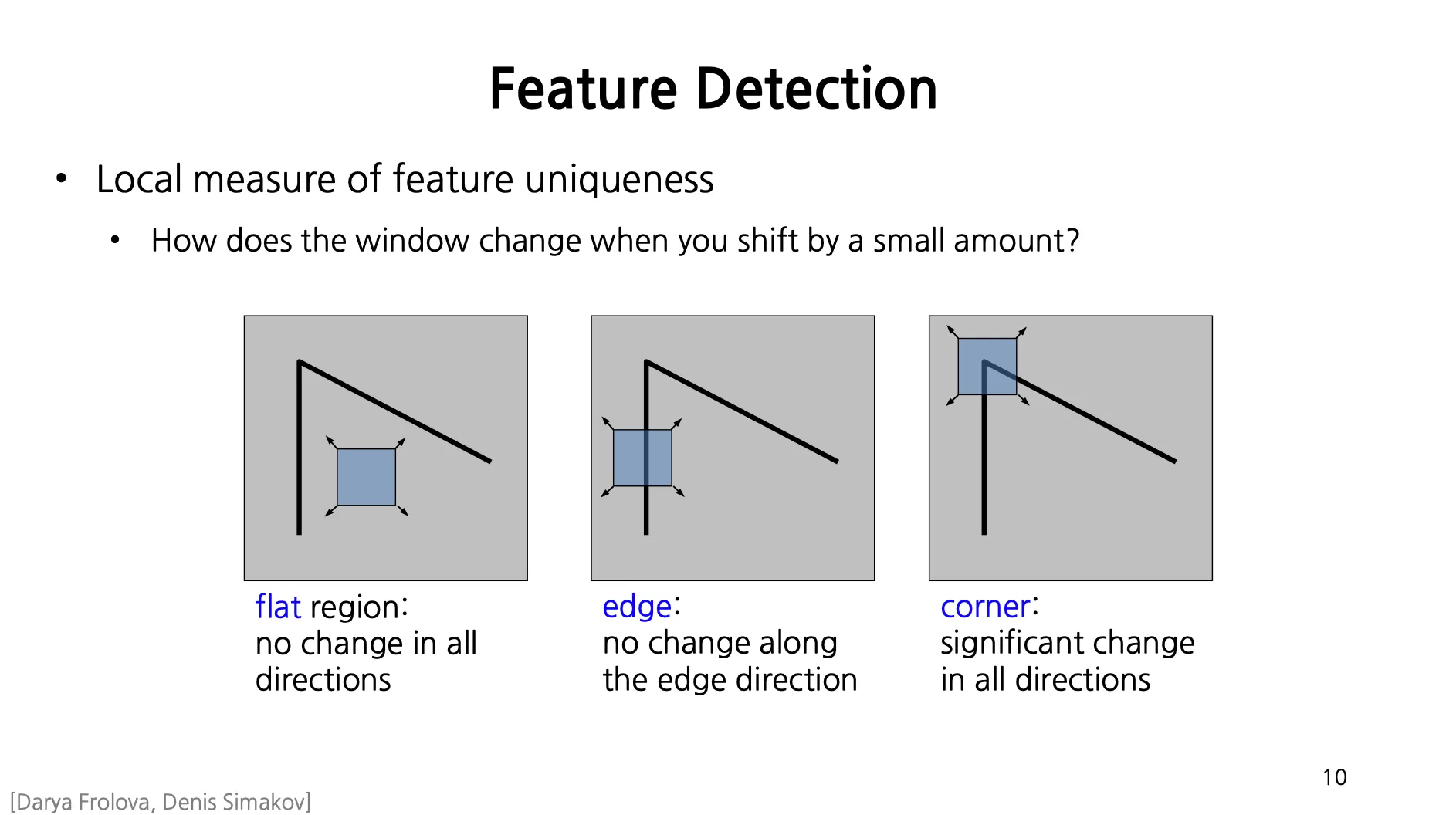
Local Measures of Uniqueness
•
특별한 영역, 지점들을 keypoints 로 잡아야하는데, 이 “특별함” 을 어떻게 정의할 것인지가 필요함.
•
어떤 지점의 특별함 (Feature Uniqueness) 을 주변의 사각형 영역을 움직였을 때, 얼마나 큰 변화가 있는지로 볼 수 있음.
◦
Flat Region: 사각형 영역을 움직여도 사각형 영역 내부의 모습이 일정함.
◦
Edge: Edge 방향으로 사각형 영역을 움직이면 사각형 영역 내부의 모습이 일정함.
◦
Corner: 임의의 방향으로 사각형 영역을 움직여도 사각형 영역 내부의 모습이 변함.
◦
가장 distinctive 하고 unusual 한 것은 Corner 임.
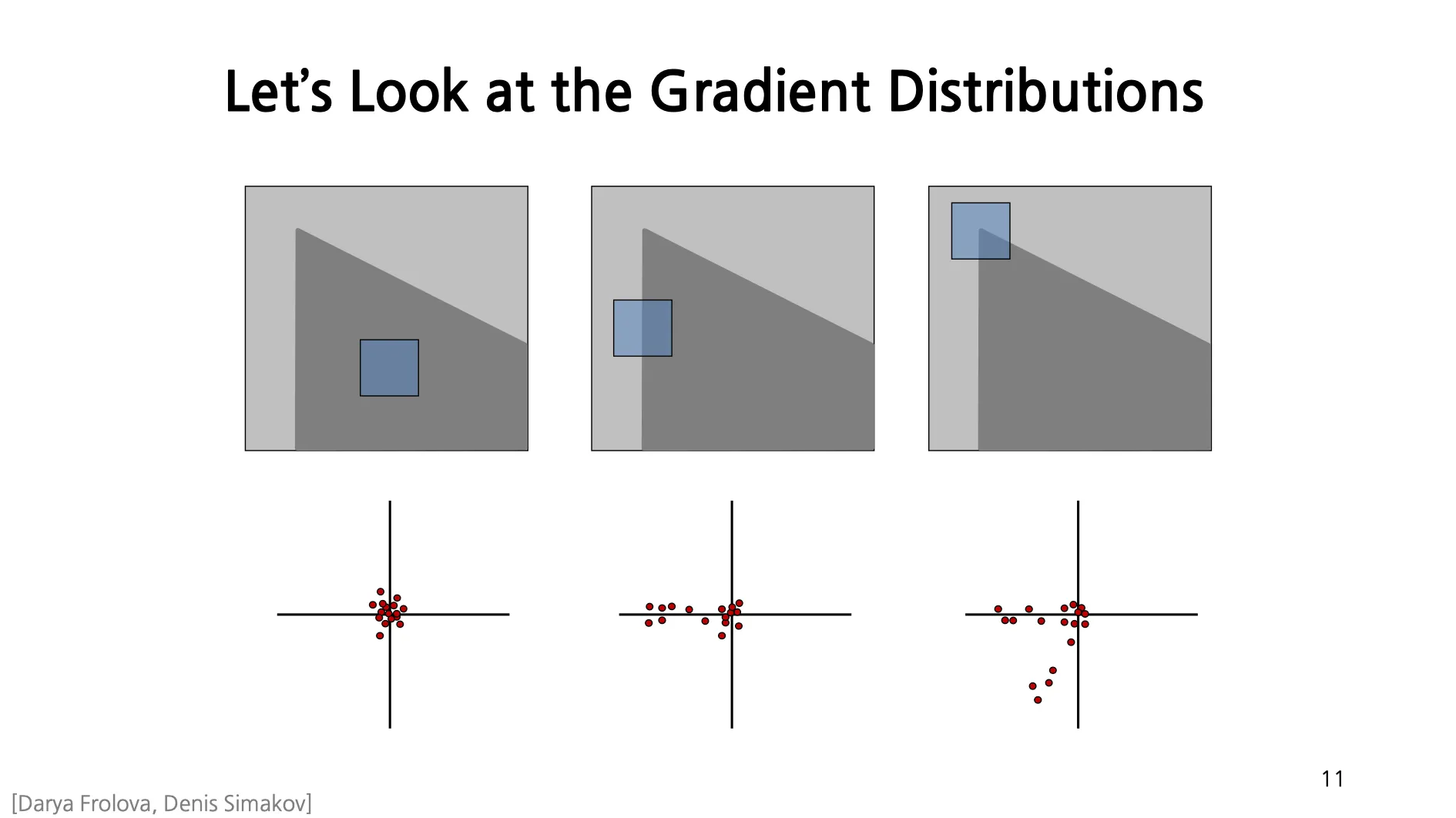
Let’s Look at the Gradient Distributions
•
Corner 와 같이 특별한 지점을 찾기 위해서 Gradient Distribution 을 활용할 수 있음.
Pinciple Component Analysis
•
두 개 이상의 지점에 대해서 Gradient 값이 큰 분포를 가지고 있으면 Corner 로 생각해볼 수 있음.
•
첫 번째 Principal Component 는 Variance 가 가장 높은 방향, 두 번째 Principal Component 는 첫 번째 Principal Component 와 수직이면서 Variance 가 가장 높은 방향 … N 번째 Principal Component 는 1 ~ N-1 번째 Principal Component 와 모두 수직이면서 Variance 가 가장 높은 방향임.
•
PCA 의 과정
◦
각 데이터에서 mean 을 빼서 mean 을 0 으로 변경함.
◦
Covariance Matrix 를 계산하고 그로부터 eigenvector 및 eigenvalue 를 얻어냄.
◦
Eigenvalue 의 크기가 큰 순서로 eigenvector 를 정렬하고 이 순서로 Principal Component 가 됨.
•
각 지점마다 사각형 영역을 잡고, 해당 영역 내의 방향 및 방향 gradient 를 계산하여 2차원 공간에 표현한 뒤에 PCA 를 거치면, 해당 지점이 Flat 인지, Edge 인지, Corner 인지 알 수 있음!
•
First eigenvalue 가 큰 값은 Edge, Second eigenvalue 까지 큰 값은 Corner 로 볼 수 있음.
•
(Additional) Independent Component Analysis (ICA) 를 사용하면 orthogonal constraint 가 없는, 순수하게 variance 가 큰 방향을 찾을 수 있음.
The Harris Operator
•
대표적인 keypoints detector
1.
Image 에 (optional 하게 blurring 을 거치고) 방향의 gradient , 방향의 gradient 를 구함.
2.
, , 를 계산함.
3.
구해낸 각각의 square of derivatives 에 Gaussian Filter 를 적용함.
4.
모든 픽셀에 대해서 다음과 같은 네 개의 값을 가져와 matrix 를 구성할 수 있음.
5.
구해낸 matrix 에 대해서 eigenvalue 를 구해냄.
•
하지만, 모든 픽셀에 대해서 해당 operation 을 통한 계산을 하는 것은 computationally expensive
•
Harris Operator 에서는 두 eigenvalue 가 모두 클 때 값이 커지는 Cornerness Function 을 정의함.
6.
Cornerness Function - Both eigenvalues are strong
•
Cornerness Function 이 큰 값은 Corner!
•
matrix 에서 determinatnt 는 두 eigenvalue 의 곱으로 나타내짐.
•
matrix 에서 trace 는 두 eigenvalue 의 합으로 나타내짐.
Maximally Stable External Regions (MSER)
•
Interest Point Detector 의 일종.
•
이미지 속에서 Stable 한 영역을 찾는 알고리즘
◦
Watershed Segmentaton Algorithm 을 기반으로 동작함.
•
Photo OCR, Text Spotting 에서 자주 사용됨.
Scale
•
Keypoint 로 지정된 영역의 범위가 얼마나 되야 적절한 것일까?
→ 영역의 안과 밖의 정보 차이가 클 때가 최적의 scale 임.
•
Laplacian 은 안쪽은 positive, 바깥쪽은 negative 이기 때문에, Laplacian 을 써서 Convolution 했을 때 안 밖의 차이가 얼마나 큰지를 확인할 수 있고 가장 큰 response 를 보이는 크기의 Laplacian 을 찾음으로써 적절한 영역을 구해낼 수 있음.
•
Automatic Scale Selection
◦
Laplacian 이 가장 크게 되는 를 잡는 아이디어를 유지했을 때, 실제로도 zoom-in 된 이미지에서는 zoom-out 된 이미지보다 가 상대적으로 클 때 Laplacian 이 최대가 되었음.
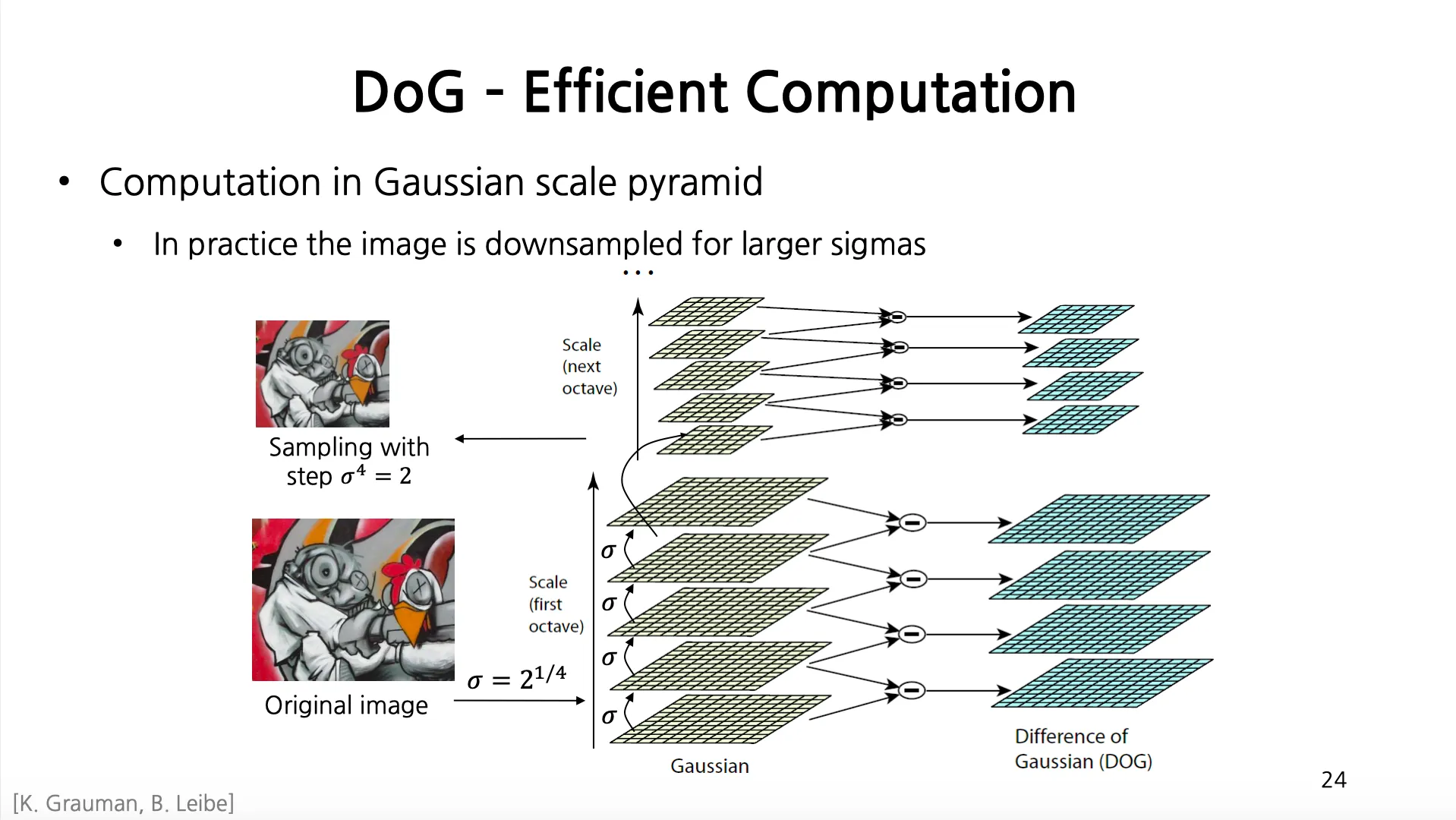
DoG - Efficient Computation
1.
Gaussian 을 적용을 4 번 거듭한뒤 로 resize 하는 것을 반복하여 Gaussian Scale Pyramid 를 만듬.
2.
두 개의 인접한 Gaussian 적용 결과를 빼주면, Difference of Gaussian 을 얻어낼 수 있음.
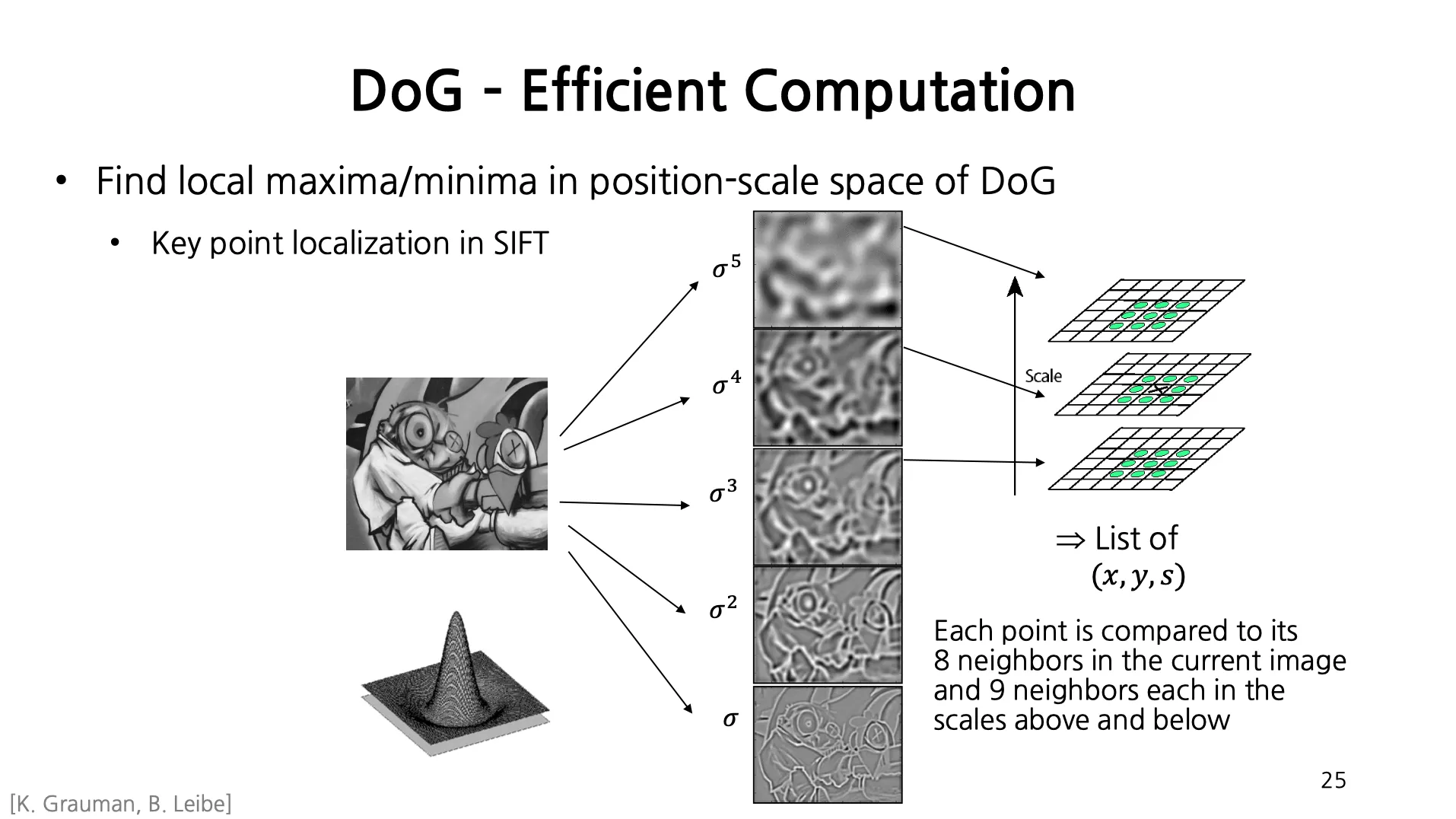
3.
특정 위치의 특정 단계의 픽셀 값이 본인 단계의 DoG 의 주변 8 픽셀과 전 및 후 단계의 DoG 의 9 픽셀들에 비해서 모두 크거나 모두 작으면 해당 scale 에서 해당 위치에서 keypoints 가 잡힌다고 볼 수 있음.
→ Keypoint 와 Scale 을 동시에 찾을 수 있음!
Rotation
•
Keypoints 영역을 정했는데, 해당 영역의 Principle Direction (Dominant Orientation) 은 어떻게 잡나?
1.
영역 안의 각 픽셀에 대해서 gradient 를 계산함.
2.
각 영역에 대해서 Angular Orientation Histogram 을 계산함.
a.
Bin 각각은 angle 의 범위를 나타내며, 각 bin 에는 해당 angle 에 속하는 gradient 를 가지는 픽셀들의 gradient magnitude 의 합이 넣어지게 됨.
b.
각 Bin 은 Histogram 의 하나의 막대를 뜻하며, 각 막대 중 가장 큰 값을 가지는 Bin 이 의미하는 angle 범위가 dominant orientation 이 됨.
Local Descriptors
•
이상적인 descriptor 들의 특징
◦
Robust: 이미지에 variation (e.g., rotation, illumniation change) 이 있다고 하더라도 동일한 keypoint 에서 잡힌 descriptor 는 동일하거나 유사해야 함.
◦
Distinctive: 다른 keypoint 에서 잡힌 descriptor 는 충분히 달라야 함.
◦
Compact: descriptor vector 의 dimension 이 작을수록 좋음.
◦
Efficient: descriptor 를 빠르게 계산할 수 있을수록 좋음.
•
많은 descriptor 들이 제안되었지만, 대부분 edge/gradient 정보에 초점을 맞추어 descriptor 를 구성함.
◦
edge/gradient 정보가 여러가지 variation 에 대해서 robust 하기 때문임.
◦
예시로 color 와 같은 정보는 조명 조건에 따라서 달라지기 때문에 robust 하지 않음.
Local Descriptors: SIFT Descriptor
•
Histogram of Oriented Gradients
◦
중요한 texture 정보를 얻어낼 수 있음.
◦
Translation 및 Affine Deformation 에도 robust 함.
Scale Invariant Feature Transform
1.
Keypoints 영역 및 scale 및 dominant orientation 을 구함.
2.
Window 를 dominant orientation 방향으로 rotate 함.
3.
Window size 를 scale 에 맞게 조정함.
4.
영역 안에 속한 픽셀에 대해서 gradient orientation 및 magnitude 를 구함.
5.
구해낸 gradient orientation 을 각 각도 영역에 대해서 angle histogram 을 만듬.
a.
총 16 개의 cell 이 생기고, 각각에 8 개의 orientation 이 있으면 128 dimensional descriptor 가 됨.
b.
각 크기는 SIFT paper 에서 empirical 하게 결정되었음.
c.
전체 keypoints 영역 () 을 세부 cell 영역 () 으로 나눈 뒤 그 영역 하나에 각각 histogram 을 만듬.
Properties of SIFT
•
의 view point change 까지는 잘 동작함.
•
Illumniation 의 큰 change 에 대해서도 잘 동작함.
•
빠르고 효율적임. (Real-Time 에서 수행할 수 있음.)
Choosing a Detector
•
어떤 Detector 를 써서 keypoints 를 찾아내야 할까?
◦
정확한 , 위치를 알고 싶다 → Harris
◦
Scale 을 정확히 뽑고 싶다 → Difference of Gaussian
◦
Flexible 하지만 uniform 한 region 을 찾고 싶다 → MSER
•
각 Detector 가 잘 동작하는 시나리오가 존재함.
◦
Harris-/Hessian-Laplace/DoG 는 Natural Categories 에 대해서 잘 동작함.
◦
MSER 은 building 이나 printed things 에 대해서 잘 동작함.
•
여러 개의 Keypoints Detector 를 사용할 수도 있음.
•
Keypoints Detector 의 성능에 대해서 비교를 한 benchmark 가 존재하여 비교해서 사용할 수 있음.
Choosing a Descriptor
•
여러개의 descriptor 를 사용해도 무방함.
•
가장 많이 사용되는 descriptor 는 SIFT, 혹은 그 variant 들임.
•
Deep Learning 은 descriptor 를 스스로 배우는 접근임.
Conclusion
•
Keypoint Detection: Repeatable and Distinctive
◦
Corner, Blobs, Stable Regions
◦
Harris, DoG
•
Descriptors: Robust and Selective
◦
Spatial Histograms of Orientation (ex. SIFT)