본 세션에서는, Deep Feed Forward Network (DFFN) 와 굉장히 유사한 형태의 네트워크인 Auto Encoder (AE)에 대해서 알아보려고 합니다.
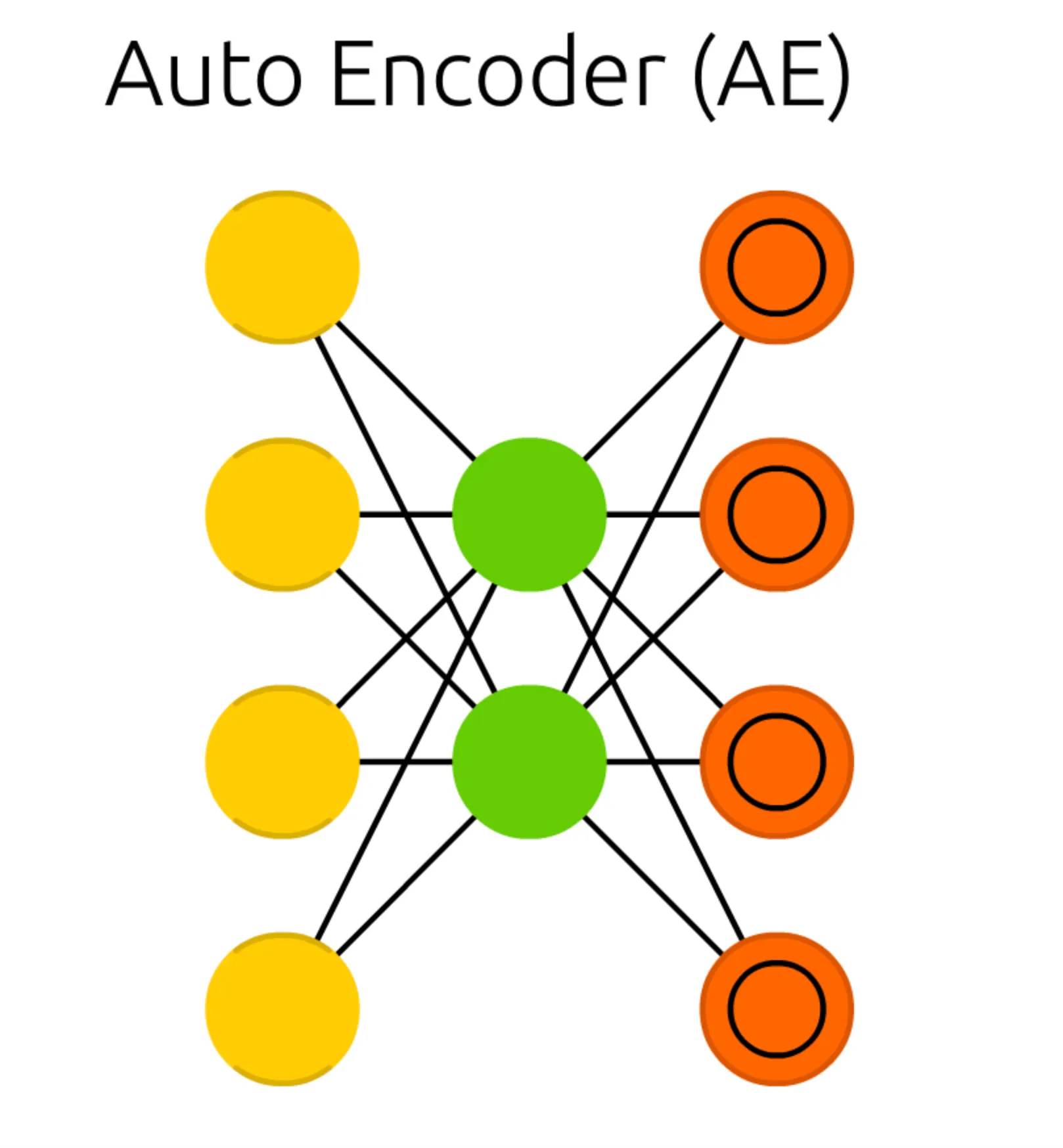
가장 먼저 보이는 구조의 특징적인 변화는 Output Cell 이 있던 위치에, 내부에 동심원이 그려진 다른 Cell 이 존재한다는 점입니다. 이러한 형태의 Cell 을 Match Input Output Cell 이라고 합니다. 더불어 이전의 RNN, LSTM, GRU 때는 지속적으로 Input Cell, Output Cell, 그리고 Memory Cell 의 개수는 구조와 관련이 없다고 말씀드렸었습니다. 하지만, Auto Encoder 에서는 이전에 설명드린 네트워크들과는 달리 Input Cell, Hidden Cell, Match Input Output Cell 간의 개수에 대한 제약 조건이 있습니다.
그렇다면, Auto Encoder 의 각 Cell 의 개수에 존재하는 제약 조건은 무엇일까요?
첫 번째 제약조건은 Match Input Output Cell 이라는 Cell 이름에서도 살펴볼 수 있습니다. Output Cell 의 vectorized form 이 Input Cell 과 매치되어야 한다는 조건입니다. 여기서 매치라 함은 dimension 이 같다고 보시면 됩니다. 위의 Auto Encoder 의 도식에서도 Cell 의 개수가 동일한 것을 볼 수 있습니다.
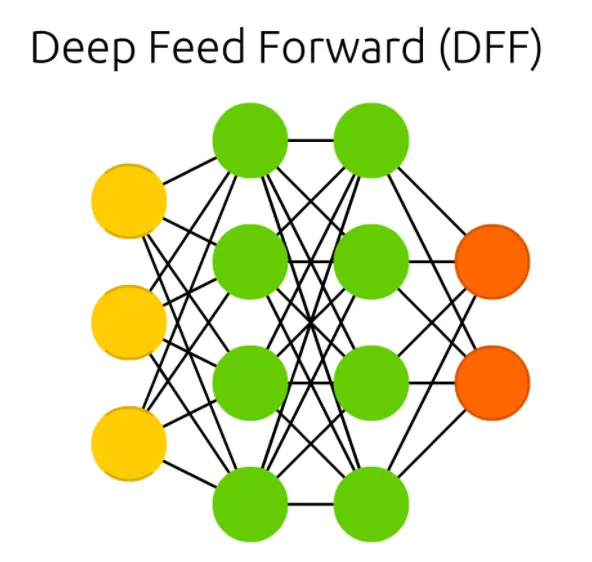
두 번째 제약조건은 Hidden Cell 의 dimension 이 Match 된 Input 및 Ouput Cell 보다 작아야 한다는 조건입니다. 기억을 상기시키기 위해 말씀드리자면 기존의 Deep Feed Forward Network (DFFN) 에서는 이와 같은 조건이 없어서 다음과 같은 형태를 지니고 있었습니다.
위 도식에서 볼 수 있는대로, Deep Feed Forward Network (DFFN) 의 경우에는 Hidden Cell 의 개수가 Input 및 Output Cell 보다 많더라도 아무런 문제가 되지 않습니다.
다만 Auto Encoder 에서는 그럴 수 없습니다.
앞서는 Auto Encoder 의 구조를 Deep Feed Forward Network 와 비교하며 설명을 드렸습니다. 간단하게 정리하자면 Auto Encoder Deep Feed Forward Network 와 구조 자체는 동일하지만, 두 가지 제약조건이 붙은 구조입니다.
그렇다면 이러한 제약 조건이 왜 필요했을까요?
이를 알기 위해서는 기존에 설명드린 네트워크들과 Auto Encoder 는 목적성이 사뭇 다른 네트워크라는 점을 아셔야 합니다.
가령, RNN 을 생각해봅시다. 이전에 RNN 을 설명드릴 때 네이버의 CLOVA 를 예시로 든 적이 있습니다.
RNN 은 CLOVA 처럼 언어모델의 구현에 사용되는 네트워크로 언어 말 뭉치를 데이터로 사용하여 해당 말 뭉치들에서 긴밀한 연결관계를 캐치해 내어 물음에 자연스러운 답을 출력할 수 있는 기능을 학습할 수 있습니다. 이처럼, 지금까지 소개드린 네트워크들은 어떤 해당 input 에 대한 conditional 한 output 을 내고 싶은데 그 관계에 대해서 명확히 "이런 관계야" 라고 말 할 수 없는 복잡한 문제를 해결하는데 사용되었습니다.
하지만, Auto Encoder 는 다릅니다. 이 친구는 input 에 대한 conditional 한 output 을 내는 것이 학습의 목적이 아닙니다. 그저 Hidden State 자체를 학습하는 것이 목적입니다.
여기까지 오시면 엥? 이건 또 무슨 소리야 하실 분들이 계실 것 같습니다. 지금까지의 Hidden State 는 그저 Input 을 Output 으로 mapping 하기 위한 수단이었을 뿐으로 이해하고 계셨기 때문입니다. Auto Encoder 에서의 Hidden State 는 단순히 Input → Output 에 대한 mapping 이 아니라, Input 을 잘 표현할 수 있는 하나의 representation (표현형) 을 만들어낼 수 있는 mapping 입니다. 조금 더 살을 덧붙이자면, Input 에 존재하는 많은 데이터들을 가공하여 핵심이 될만한 데이터 feature 들을 추출하여 Input 데이터의 표현형인, latent vector 로 나타낸다고 보시면 됩니다.
그리고, 이러한 latent vector 가 가져야 할 중요한 특성이 데이터의 복원가능성입니다. Latent vector 가 해당 데이터의 좋은 representation 이라면, 그 표현형만으로 원본 데이터를 재구성하는 작업이 가능해야 한다- 는 논리인 것입니다. Auto Encoder 에서는 이 특성을 가지는 vector 를 만들어 내기 위해 Hidden State 를 학습하는 것입니다.
지금까지, Auto Encoder 의 목적에 대해서 알아보았습니다. 제약 조건의 필요성을 언급하다가 Auto Encoder 의 목적을 이야기 드렸는데요, 눈치 빠르신 분들은 제약 조건의 필요성도 이제 어느정도 아셨을 것 같습니다.
원본 데이터의 복원 가능성을 latent vector 의 주요 feature 로 보고 해당 기능을 잘 수행할 수 있는 latent vector 를 생성하는 네트워크 구조를 만들기 위해서는 해당 기능을 얼마나 잘 수행하는가에 대한 기준이 있어야 합니다. 그리고, 이 기준은 학습에서 loss function 이 되는 것입니다.
Auto Encoder 에서는 Input 과 Output 이 얼마나 동일한가? 를 가지고 loss function 을 정의합니다. 이 때 유사도를 정의하는 기준으로 각 pixel 단위의 MSE 를 사용합니다.
여기서 N 은 전체 픽셀의 수라고 보시면 되겠습니다. RGB 형태의 이미지의 경우에는 size 의 3 배만큼의 값입니다. 결과적으로 해당 loss function 의 최소화를 목표로 gradient descent 를 적용하게 되면 Input 과 Output 의 픽셀 값이 유사하도록 학습이 진행됩니다.
이러한 설계 때문에 기본적인 Auto Encoder 는 필연적으로 Input 과 동일한 Output 이 나오기를 기대하면서 학습을 진행하고, Input Cell 과 Output Cell 의 dimension 이 같다는 제약 조건이 붙게 되는 것입니다.
그렇다면, Hidden Cell 의 dimension 이 Match 된 Input 및 Ouput Cell 보다 작아야 한다는 조건은 왜 필요한 것일까요?
간단하게 대답하자면, 반대로 생각해보면 됩니다. Hidden Cell 의 dimension 이 Match 된 Input 및 Ouput Cell 보다 크다면 네트워크가 학습하게 될 mapping 이 identity mapping 일 수도 있습니다. 즉, latent vector 가 Input Cell 과 동일한 채 zero-padding 만 추가된, 의미 없는 값일 수도 있다는 것입니다. Auto Encoder 에서 이러한 현상을 원했던 것은 당연히 아닐 것입니다.
하지만, 보다 정확한 대답은 latent vector 의 근본에 있습니다. Auto Encoder 에서 latent vector 를 생성하려고 했던 근본적인 이유는 차원의 저주라고도 불리는 The Curse of Dimensionality 문제를 해결하기 위해서입니다.
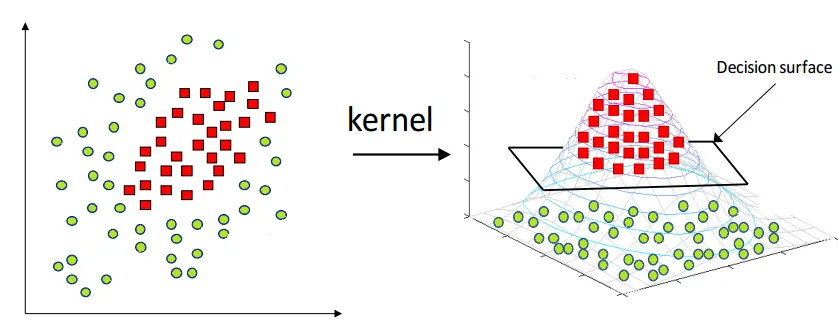
같은 수의 Input 데이터가 있다고 가정해봅시다. 그런데 한 경우는 Input 데이터의 차원이 2차원이고 한 경우는 3차원입니다. 이전에 Radial Basis Function Network 에서 설명드린 kernel 을 사용한 차원 확대 그림을 다시 가져와보겠습니다.
기존에는 데이터를 분리할 수 있는 결정 경계를 쉽게 찾을 수 있도록 고차원으로 mapping 하는 kernel function 을 적용하여 차원 확대의 이점을 살리는 예시를 보여드렸었습니다. 하지만 차원 확대가 이점만 있는 것은 아닙니다. 동일한 데이터의 수를 가진다고 가정했을 때 해당 차원의 vector space 에서 데이터가 설명가능한 영역의 범위가 줄어드는 효과를 발생시킵니다.
즉, 차원이 늘어나면 늘어날수록 해당 vector space 속에서 데이터가 가지는 의미를 캐치하기 위해서는 더 많은 수의 데이터가 필요한데 일반적으로 데이터의 수를 차원의 수에 비례해서 쉽게 늘릴 수 없기 때문에 반대로 데이터에서 그 데이터를 표현하는 주요 성분만을 뽑아내는 형태로 차원을 축소한다고 보시면 됩니다.
여담으로, 해당 차원 축소는 PCA 등의 방법도 있으니 참고하시면 좋을 것 같습니다.
정리하자면, latent vector 를 만드려는 근본적인 이유가 데이터의 표현 형태를 저차원으로 낮추어 적은 데이터에서의 학습효율을 늘린다고 보시면 됩니다. 때문에 필연적으로 latent vector 는 Input 보다 dimension 이 낮아야 합니다.
마지막으로, Auto Encoder 의 활용에 대해서 간단하게 언급하고 넘어가려고 합니다.
위의 북마크에 있는 내용에 따르면 denoising 및 anomaly detection 등을 활용할 수 있다고 합니다.
Auto Encoder 의 주목적은 앞서 언급했듯이 latent vector 의 생성입니다. 그리고 이러한 latent vector 의 생성은 Input Data 의 차원을 낮추어주는 encoder 의 역할입니다. 그렇다면 latent vector 로부터 원본 이미지를 복원하는 과정을 진행하는 decoder 는 아무런 의미가 없는 걸까요?
Auto Encoder 에서는 그렇습니다.
다만 다음에 설명드릴 Variational Auto Encoder 는 반대로, decoder 가 의미가 있고, encoder 가 의미가 없어집니다. 몇몇 분들은 예상하시겠지만, Generative Model 의 시작입니다.
이렇게 이번 세션에서는 Auto Encoder (AE) 에 대해서 알아보는 시간을 가졌습니다. Auto Encoder 의 목적이 latent vector 의 추출이고, 이러한 latent vector 의 추출은 근본적으로 The Curse of Dimesionality 를 해결하기 위함이라는 것을 알고 계시면 될 것 같습니다.