Lecture 20 | Lucas-Kanade Tracking

수강 일자

2022/11/15

Newton’s Method

•

주어진 함수 f(x)=0f(x)=0f(x)=0 을 만족하는 해를 찾는 방법론

•

가장 naive 한 approach 는 Δx\Delta xΔx 를 정의하고 해당 크기만큼 변형해가면서 함수값을 측정하는 것

◦

양에서 음, 음에서 양으로 변하는 지점에서 해가 존재함.

◦

단점

▪

Δx\Delta xΔx 가 너무 작은 경우에는 알고리즘이 오래걸림.

▪

Δx\Delta xΔx 가 너무 크면 해가 2개 있을 때 하나만 찾고 지나쳐버릴 수도 있음.

•

Newton’s Method

적절한 initial guess x0x_0x0​ 에서 시작점을 잡음.

f(x)f(x)f(x) 를 해당 initial guess point 를 기준으로 tangent line 으로 근사하여 해석함

y = f'(x_n) (x-x_n)+f(x_n)

근사한 tangent line 의 해를 다음 guess x1x_1x1​ 으로 설정함.

0=f'(x_n)(x_{n+1}-x_n) +f(x_n)\\ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

수렴할 때까지 1 ~ 3 을 반복함.

•

Optimization 문제를 풀 때 해를 구하는 것을 중요한 과정이 됨.

◦

Minimize g(x)g(x)g(x) → Find root for f(x)=g′(x)=0f(x) = g'(x)=0f(x)=g′(x)=0

General Problem of Image Registration

•

Template Image T(x)T(x)T(x) 와 Input Image I(x)I(x)I(x) 가 주어짐.

•

Image Registration 문제의 종류들은 다음과 같은 것들이 있었음.

Image Alignment: 한 이미지 I(x)I(x) I(x) 에서 다른 이미지 T(x)T(x)T(x) 로 warping 하여 가장 좋은 match 를 찾는 경우

Tracking: T(x)T(x)T(x) 는 ttt 시각에 ppp 점 근처의 (tracking 하고자 하는) 작은 영역 이고, I(x)I(x)I(x) 는 t+1t+1t+1 시각의 이미지인 경우

Optical Flow: T(x)T(x)T(x) 와 I(x)I(x)I(x) 각각이 ttt, t+1t+1t+1 시각의 이미지 영역이고 움직임을 시각정보만으로 예측하는 경우

•

카메라가 이동하면서 물체를 찍은 경우에는, 바뀐 카메라의 image plane 상으로 warping 을 한 다음에 matching 을 하는 것이 올바른 순서임.

Simple Approach (for Translation)

•

Sum of Squared Distances 를 최소화하는 uuu, vvv 를 구함.

E(u,v) = \sum_{x,y} (I(x+u,y+v)-T(x,y))^2

•

단점

◦

효율적인 알고리즘이 아님. (III 상의 모든 location 에 대해서 SSD 를 모두 구해야 하기 때문임)

◦

Sub-pixel Accuracy 를 측정할 수 없음. (픽셀 단위 이하의 정확도를 구할 수 없음)

Lucas-Kanade Tracking

•

Object Tracking

E(u,v) = \sum_{x,y} (I(x+u,y+v)-T(x,y))^2

◦

이전 frame 에 대해서 이미지 내에서 template 의 위치가 주어졌을 때, 다음 frame 에서의 template 의 위치를 구하는 문제

•

Frame 간 간격이 좁다고 가정하면 uuu, vvv 가 작다고 가정할 수 있고, Taylor Expansion 을 적용해볼 수 있음.

I(x+u,y+v) \approx I(x,y) + uI_x + vI_y

•

원래 Sum of Squared Distance 식에 위의 변형을 대입하면 다음과 같음.

\sum_{x,y} (I(x,y)-T(x,y)+uI_x +vI_y)^2

•

SSD 를 최소화하기 위해 미분하면 다음과 같음.

0 = \frac{\partial E}{\partial u} = \sum_{x,y}2I_x[I(x,y)-T(x,y)+uI_x+vI_y]\\ 0 = \frac{\partial E}{\partial v} = \sum_{x,y}2I_y[I(x,y)-T(x,y)+uI_x+vI_y]

•

위 식을 uuu, vvv 만 LHS 에 남기면 다음과 같이 변형할 수 있음.

\sum_{x,y}I_x^2 u + \sum_{x,y}I_xI_y v= \sum_{x,y}I_x(T(x,y)-I(x,y)) \\ \sum_{x,y}I_xI_y u + \sum_{x,y}I_y^2 v= \sum_{x,y}I_y(T(x,y)-I(x,y)) \\

•

최종적인 Matrix Form 으로 다음과 같이 표현할 수 있음.

\begin{bmatrix} \sum_{x,y} I_x^2 & \sum_{x,y} I_xI_y \\ \sum_{x,y} I_xI_y & \sum_{x,y} I_y^2 \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \sum_{x,y} I_x(T(x,y)-I(x,y)) \\ \sum_{x,y} I_y(T(x,y)-I(x,y)) \\ \end{bmatrix}

One Problem with Lucas-Kanade

•

Initial frame 에 대해서 Tracking 하고자 하는 object 가 template 이 되어서 연속적인 frame 에서 찾아가는 방법인데, 물체를 바라보는 viewpoint 가 바뀌면 잘 동작하지 않음. 

•

Warping 까지 고려한 일반화된 Lucas-Kanade Tracking 이 필요함.

\sum (I(x+u, y+v)-T(x,y))^2 \rarr\sum[T(x)-I(W(x;p))]^2

◦

ppp 라는 parameter 를 가지는 warping 을 이용해서 point xxx 를 변환시키고 해당 warped image plane 상에서의 위치 차이를 계산함.

◦

좋은 warping parameter 인 ppp 를 계속 찾아나가야 함. (ppp 로 정의되는 warping 은 translation 은 물론 homography 를 포함하기 때문에 uuu, vvv 를 포함하는 일반적인 개념임)

Lucas-Kanade Algorithm (Generalized ver.)

•

I(W(x;p))I(W(x;p))I(W(x;p)) 와 T(x)T(x)T(x) 의 SSD 를 최소화하하도록 align 하는 warping parameter ppp 를 찾아야 함.

E(u,v)= \sum (I(x+u, y+v)-T(x,y))^2 \\ \rarr E(p) =\sum[I(W(x;p))-T(x)]^2

◦

E(p)E(p)E(p) 를 최소화하는 ppp 를 찾아야 함

•

Examples

◦

Warping = Translation

W(x;p)=\begin{pmatrix} x +d_x\\ y+d_y \end{pmatrix}, \quad p= \begin{pmatrix} d_x\\ d_y \end{pmatrix}

◦

Warping = Affine

W(x;p)=Ax+d = \begin{pmatrix} 1+d_{xx} & d_{xy} & d_x \\ d_{yx} & 1+d_{yy} & d_y \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}

p = \begin{pmatrix} d_{xx} & d_{xy} & d_{yx} & d_{yy} & d_x & d_y \end{pmatrix}^T

•

WWW 가 ppp 에 대한 선형적인 함수로 표현이 되지 않기 때문에 Non-Linear Optimization 을 풀어야 함.

•

Tracking 같은 경우에는 많은 경우에 Affine Transform 으로 가정해도 충분함. → 6DoF

◦

처음 시작 위치에서는 Template 의 위치가 주어지기 때문에 p=0p=0p=0 으로 설정함.

◦

다음 시각 때부터는 정확한 ppp 가 아닌 Δp\Delta pΔp 에 대해서 구함.

Parametric Model

{\rm Minimize}\quad \sum_x [I(W(x;p)-T(x)]^2 \quad {\rm w.r.t.}\Delta p

•

First Order Taylor Expansion 을 적용하여 WWW 를 변경할 수 있음.

W(x;p+\Delta p)\approx W(x;p) + \frac{\partial W}{\partial p}\Delta p

•

W(x;p)W(x;p)W(x;p) 에 비해서 ∂W∂pΔp\frac{\partial W}{\partial p}\Delta p∂p∂W​Δp 항목이 충분히 작다는 가정 하에서 다시 한 번 First Order Taylor Expansion 을 사용할 수 있음.

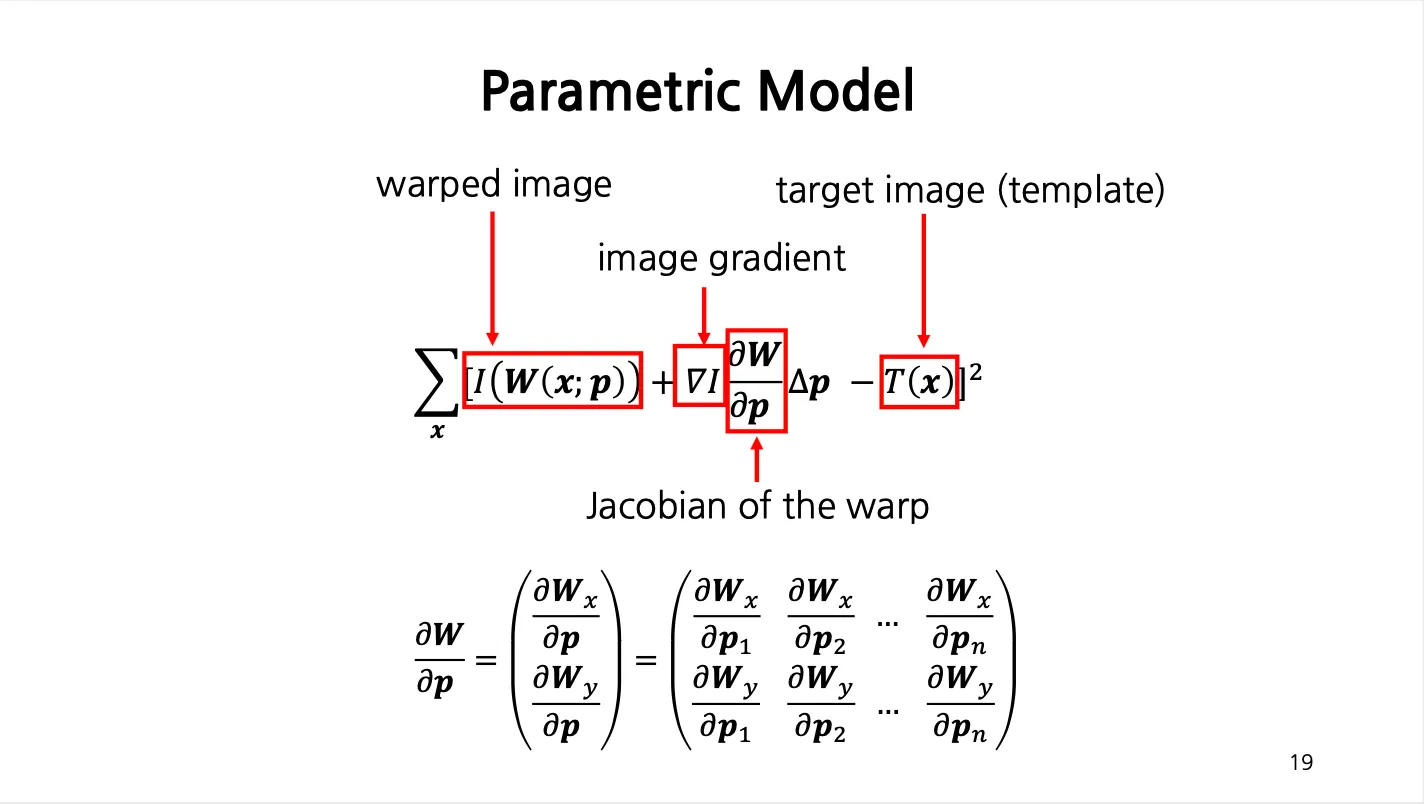
I(W(x;p+\Delta p)) \approx I(W(x;p)+\frac{\partial W}{\partial p}\Delta p) \approx I(W(x;p))+\frac{\partial I}{\partial x}\frac{\partial W}{\partial p}\Delta p

•

최종적인 목표는 다음과 같이 변형됨.

{\rm Minimize}\quad \sum_x [I(W(x;p) + \nabla I\frac{\partial W}{\partial p}\Delta p -T(x)]^2

Jacobian Matrix

•

f:R→Rf:{\mathbb R} \rarr {\mathbb R}f:R→R 에 대한 미분은 derivative

•

f:Rn→Rf:{\mathbb R}^n \rarr {\mathbb R}f:Rn→R 에 대한 미분은 gradient

•

f:Rn→Rmf:{\mathbb R}^n \rarr {\mathbb R}^mf:Rn→Rm 에 대한 미분은 jacobian

J_F(x_1, x_2,\dots, x_n) = \begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \dots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \dots & \frac{\partial f_m}{\partial x_n} \end{pmatrix}

F(x+\Delta x) \approx F(x) + J_F(x) \Delta x

Jacobian of the Warp

\frac{\partial W}{\partial p} = \begin{pmatrix} \frac{\partial W_x}{\partial p} \\ \frac{\partial W_y}{\partial p} \end{pmatrix} = \begin{pmatrix} \frac{\partial W_x}{\partial p_1} & \frac{\partial W_x}{\partial p_2} & \dots & \frac{\partial W_x}{\partial p_n} \\ \frac{\partial W_y}{\partial p_1} & \frac{\partial W_y}{\partial p_2} & \dots & \frac{\partial W_y}{\partial p_n} \end{pmatrix}

•

Example - Affine Transform

W(x;p)= \begin{pmatrix} 1+d_{xx} & d_{xy} & d_x \\ d_{yx} & 1+d_{yy} & d_y \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} (1+d_{xx})x + d_{yy}y+d_x \\ d_{yx}x + (1+d_{yy})y + d_y \end{pmatrix}

p = \begin{pmatrix} d_{xx} & d_{xy} & d_{yx} & d_{yy} & d_x & d_y \end{pmatrix}^T

\frac{\partial W}{\partial p} = \begin{pmatrix} x & 0 & y & 0 & 1 & 0 \\ 0 & x & 0 & y & 0 & 1 \end{pmatrix}

Parametric Model

{\rm Minimize}\quad \sum_x [I(W(x;p) + \nabla I\frac{\partial W}{\partial p}\Delta p -T(x)]^2 \\ \rarr 0 = \sum_x [\nabla I \frac{\partial W}{\partial p}]^T[I(W(x;p))+ \nabla I\frac{\partial W}{\partial p}\Delta p -T(x)]\\ \rarr \Delta p = H^{-1}\sum_x [\nabla I \frac{\partial W}{\partial p}]^T [T(x)-I(W(x;p))] \\

•

Δp\Delta pΔp 에 대한 편미분을 통해 minimum 을 찾음.

•

Δp\Delta pΔp 만 LHS 에 남기고 식을 정리하면 위와 같이 나타남.

H = \sum_x [\nabla I \frac{\partial W}{\partial p}]^T[\nabla I \frac{\partial W}{\partial p}]

•

각각의 step 마다 Δp\Delta pΔp 를 위와 같은 식으로 구해냄.

Lucas-Kanade Algorithm

Warp III with W(x;p)W(x;p)W(x;p) to I(W(x;p))I(W(x;p))I(W(x;p))

Compute error image T(x)−I(W(x;p))T(x) -I(W(x;p))T(x)−I(W(x;p))

Warp gradient of III to compute ∇I\nabla I∇I

Evaluate Jacobian ∂W∂p\frac{\partial W}{\partial p}∂p∂W​

Compute Hessian H=∑x[∇I∂W∂p]T[∇I∂W∂p]H=\sum_x [\nabla I \frac{\partial W}{\partial p}]^T[\nabla I \frac{\partial W}{\partial p}]H=∑x​[∇I∂p∂W​]T[∇I∂p∂W​]

Compute Δp\Delta pΔp, Δp=H−1∑x[∇I∂W∂p]T[T(x)−I(W(x;p))]\Delta p = H^{-1}\sum_x [\nabla I \frac{\partial W}{\partial p}]^T [T(x)-I(W(x;p))]Δp=H−1∑x​[∇I∂p∂W​]T[T(x)−I(W(x;p))]

Update parameters p←p+Δpp \larr p + \Delta pp←p+Δp

Tracking Facial Mesh Models

•

Active Appearance Model 로, Face Tracking 에 많이 씀.

얼굴에 많은 landmark point 및 mesh 를 가정함

Deformation 을 허용하되, 많이는 허용하지 않는 채로 움직임을 tracking 함.

Errors in Lukas-Kanade

•

가정이 위반될 때 오류가 발생함.

Brightness Consistency 가 지켜지지 않을 경우 (corresponding point 가 다음 frame 에서 다르게 보이는 경우)

Taylor Expansion 이 적용되지 않는 경우 - The motion is not small

Occlusion 이 있는 경우 