Radial Basis Network (RBF)

태그
Basic Perceptron
포스팅 날짜
2021/05/23
본 세션에서는, Feed Forward(FF) 와 같이 XOR 문제를 풀 수 없었던 현상을 타개하기 위해 고안된 네트워크인 Radial Basis Network(RBFN) 에 대해서 알아보려고 합니다.
가장 먼저 보이는 구조의 변화는.... 무려 없습니다. Radial Basis Network(RBFN) 는 Feed Forward(FF) 와 완벽히 동일한 구조를 가지고 있습니다. Input Cell, Output Cell, 그리고 그 사이의 Hidden Cell 구조를 동일하게 가지고 있습니다.
그렇다면, Radial Basis Network 는 무슨 이유로 탄생하게 되었을까요?
좁게 보자면, Feed Forward 가 탄생한 배경과 같이 XOR 문제를 해결할 수 없었던 것이 이유이고, 넓게 보자면 낮은 차원에서 기존의 Perceptron 을 비롯한 neural network 의 dot product 연산이 가지는 linearity 만으로 해결할 수 없는 문제들을 해결하기 위해서입니다.
이에 대해서 구체적으로 살펴보기 위해서 kernel 에 대한 개념을 알 필요가 있습니다.
어떤 vector space XX 와 VV 에 대해 XX 의 임의의 두 vector x,x′\mathrm{x},\mathrm{x'} 에 대해서 feature map φ:X→V\varphi:X\rarr{V} 가 존재하여 K(x,x′)K(\mathrm{x},\mathrm{x'}) 가 VV 에 속한 두 vector φ(x),φ(x′)\varphi{(x)}, \varphi{(x')} 의 inner product 로 나타내질 수 있는 함수 KK 를 kernel 이라고 합니다. 즉, kernel function 은 다음과 같은 관계로 정의됩니다.
K(x,x′)=⟨φ(x),φ(x′)⟩VK(x,x')=\left\langle \varphi{(x)},\varphi{(x')}\right\rangle_V
간단한 예시를 들어보겠습니다.
XX 를 2-dimension euclidean vector space 로, VV 를 3-dimension euclidean vector space 로 두고, feature map φ\varphi 를 φ(x)=φ(x1,x2)=(x12,2x1x2,x22)\varphi(x)=\varphi(x_1,x_2)=(x_1^2,\sqrt{2}x_1x_2,x_2^2) 으로 정의합시다. 이 조건에서 kernel 은 다음과 같이 표현할 수 있습니다.
K(x,x′)=⟨φ(x),φ(x′)⟩V=φ(x)⋅φ(x′)=φ(x1,x2)⋅φ(x1′,x2′)=(x12x1′2,2x1x2x1′x2′,x22x2′2)K(x,x')=\left\langle \varphi{(x)},\varphi{(x')}\right\rangle_V=\varphi{(x)}\cdot\varphi{(x')}\\=\varphi{(x_1,x_2)}\cdot\varphi{(x_1',x_2')}=(x_1^2x_1'^2,2x_1x_2x_1'x_2',x_2^2x_2'^2)
이렇게 식으로 보면 이해가 잘 되지 않을 수 있습니다. 그리고 어찌보면 위 식은 당연한 결과를 풀이한 것이 아닌가? 라는 생각이 드실 수 있습니다.
이런 의문을 풀어드리기 위해 덧붙이자면, 보통의 경우에는 kernel function 에 대한 가설을 먼저 세우고 이것이 실제로 kernel function 임을 보이기 위해서 feature map φ\varphi 를 찾는 방식으로 많이 사용을 합니다. 그리고 반대로, 특정한 함수가 kernel function 이라는 것은 vector space XX 에서 VV 로의 mapping 관계 φ\varphi 가 존재하여 변환 후 space 인 VV 에서의 inner product 를 변환 전 space XX 로 부터 연산할 수 있게하는 관계를 나타낼 수 있다는 것을 의미합니다.
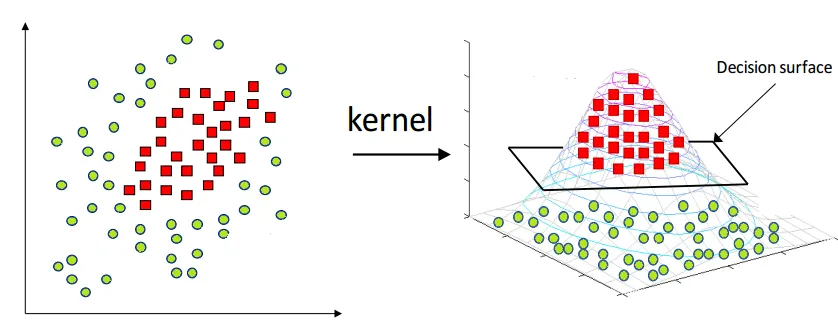
간단한 예시로 아래와 같은 그림을 들 수 있습니다. 보통의 경우 kernel 을 차원의 확대 용도로 사용해 아래와 같이 decision surface 를 원활하게 설정할 수 있도록 하기 위해 사용합니다. 이 처럼 저차원의 데이터를 고차원으로 변환하여 이를 구분하는 선형 초평면을 찾아내는 방법론을 kernel trick 이라고 합니다.
위에서 설명드린 내용 중 inner product 에 주목해야 합니다. 앞서 살펴본 Perceptron, Feed Forward 에 거쳐서 forward propagation 을 진행할 때 sum of product 를 계산했었습니다. 이 때 진행한 product 가 inner product 였습니다. 결국, neural network 관점에서 kernel 은 다른 vector space 를 만들어 그 space 에서의 inner product 를 정의하는 함수인 것입니다. 그리고, 일반적인 neural network 에서 사용하는 inner product 를 사용하는 반면에 지금 설명드릴 Radial Basis Function Network 는 특별한 kernel 인 radial basis function kernel 을 사용합니다.
Radial Basis Function Kernel 은 Gaussian Kernel 이라고도 불리는데, 이는 저희가 흔히 아는 gaussian distribution 의 지수항과 닮아 있기 때문입니다.
KRBF(x,x′)=e−γ∥x−x′∥2K_{RBF}(x,x')=e^{-\gamma\lVert x-x' \rVert^2}
보시는 것 처럼 기존의 gaussian distribution 의 지수항에서 분산 부분이 상수인 γ\gamma 로 빠지게 되고, 평균 부분이 다른 vector 로 치환된 것을 보실 수 있습니다. 이 Radial Basis Function Kernel 이 앞서 inner product 의 형태가 된다고 말씀드렸습니다. 실제로, 이 kernel 은 Radial Basis Function Network 에서 제일 첫 Layer 에 해당하는 부분의 inner product 연산 대신에 들어가게 됩니다.
즉, 기존에 weight 로 주어졌던 학습 parameter 가 Radial Basis Function Network 에서는 x′x' 으로 정의된 어떤 vector 가 되는 것입니다. 그리고 그 벡터와 input vector 와의 Radial Basis Function Kernel 연산으로 Hidden Cell 의 값을 계산하게 되는 것입니다.
먼저, 이러한 설계가 가지는 정성적인 의미부터 들여다 볼 수 있습니다. 눈치채실 분들은 이미 아시겠지만, 각 Cell 이 가지는 값은 Input Cell 의 값이 저희가 설정한 vector 와 얼마나 떨어져 있는지에 대한 척도입니다. 가까울수록 값이 크고, 멀수록 값이 작아집니다. 이러한 설계를 통해서 저희는 거리의 기준이 될 vector 를 유동적으로 조절해가며 각 input 을 그 위치에 따라 선택적으로 가중화할 수 있게 됩니다.
선택적 가중화를 하는 예시로, 처음에 이야기를 꺼냈던 XOR 문제를 꺼낼 수 있습니다. 앞서 Radial Basis Function Network 도 Feed Forward 와 같이 XOR 문제를 Perceptron 으로 풀 수 없었던 현상을 해결하기 위해서 나타난 것이라고 설명드렸습니다. 지금부터는 input 의 위치에 따른 선택적 가중화를 통해 어떻게 Radial Basis Function Network 가 XOR 문제를 풀 수 있었는지에 대해 설명드리려고 합니다.
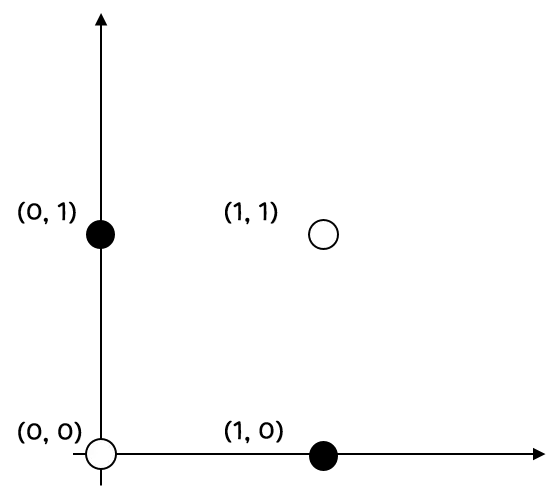
XOR 문제는 위와 같은 그래프의 점들을 색깔별로 나누는 문제였습니다. (1, 0) 과 (0, 1) 은 1 이라는 결과를 산출해야하고, (0, 0) 과 (1, 1) 은 0 이라는 결과를 산출해야만 합니다. 이를 단순히 Perceptron 으로 나누기에는 직선으로 이 둘의 경계를 정확히 구분 지을 수 없었습니다.
하지만, Radial Basis Function Kernel + Perceptron 인 Radial Baiss Function Network 의 경우는 가능합니다. Kernel 계산의 기준이 되는 vector 각각을 (0, 1) 과 (1, 0) 으로 설정해봅시다. 그렇다면, 두 Hidden Cell 의 값, 즉 Radial Basis Function Kernel 를 거친 값을 φ1,φ2\varphi_1, \varphi_2 라고 해보면, 각 지점마다의 φ1,φ2\varphi_1, \varphi_2 값은 다음과 같습니다.
(0, 0) - φ1=1e∼0.3679, φ2=1e∼0.3679,\varphi_1= \frac{1}{e} \sim 0.3679, \space \varphi_2= \frac{1}{e} \sim 0.3679,
(0, 1) - φ1=1, φ2=1e2∼0.1353,\varphi_1= 1 , \space \varphi_2= \frac{1}{e^2} \sim 0.1353,
(1, 0) - φ1=1e∼0.3679, φ2=1e∼0.3679,\varphi_1= \frac{1}{e} \sim 0.3679, \space \varphi_2= \frac{1}{e} \sim 0.3679,
(1, 1) - φ1=1e2∼0.1353, φ2=1\varphi_1= \frac{1}{e^2} \sim 0.1353, \space \varphi_2= 1
이 때 기존의 Perceptron 의 input 이 Input Cell 의 x(i)x^{(i)} 였다면, 지금의 경우에는 φ(x(i))\varphi(x^{(i)}) 입니다. 즉, 위 식의 φ1,φ2\varphi_1, \varphi_2 가 각각 Perceptron 입장에서의 Input Cell 역할을 하는 것입니다.
이 때, Percpetron 에서 저희는 sigmoid 와 BCE loss 를 사용하여 Wx(i)+bWx^{(i)}+b 가 0보다 크면 1을, 작으면 0을 산출하도록 하는 예제를 작성한 적이 있습니다. 이 때와 같은 조건을 적용하여 적절한 WW 를 구할 수 있을지를 살펴볼까요?
놀랍게도, w1=e2, w2=e2, ,b=−e2w_1=e^2,\space w_2=e^2,\space, b=-e^2 으로 설정하면 (0, 1) 과 (1, 0) 에 대해서는 Wx(i)+bWx^{(i)}+b 계산 값이 11 로 0 보다 크며, (0, 0) 과 (1, 1) 에 대해서는 Wx(i)+bWx^{(i)}+b 계산 값이 2e−e2=e(2−e)2e-e^2=e(2-e) 으로 0 보다 작습니다. (e가 2보다 크기 때문입니다) 결국 위와 같은 kernel 을 적용한 이후에는 뒤에 Perceptron 을 사용하더라도 적절한 w1w_1 과 w2w_2 가 존재하여 해가 존재하는 문제로 변한다는 것입니다. Radial Basis Function Network 에서는 이러한 형태로 XOR 문제에 대한 해답을 찾아내게 됩니다.
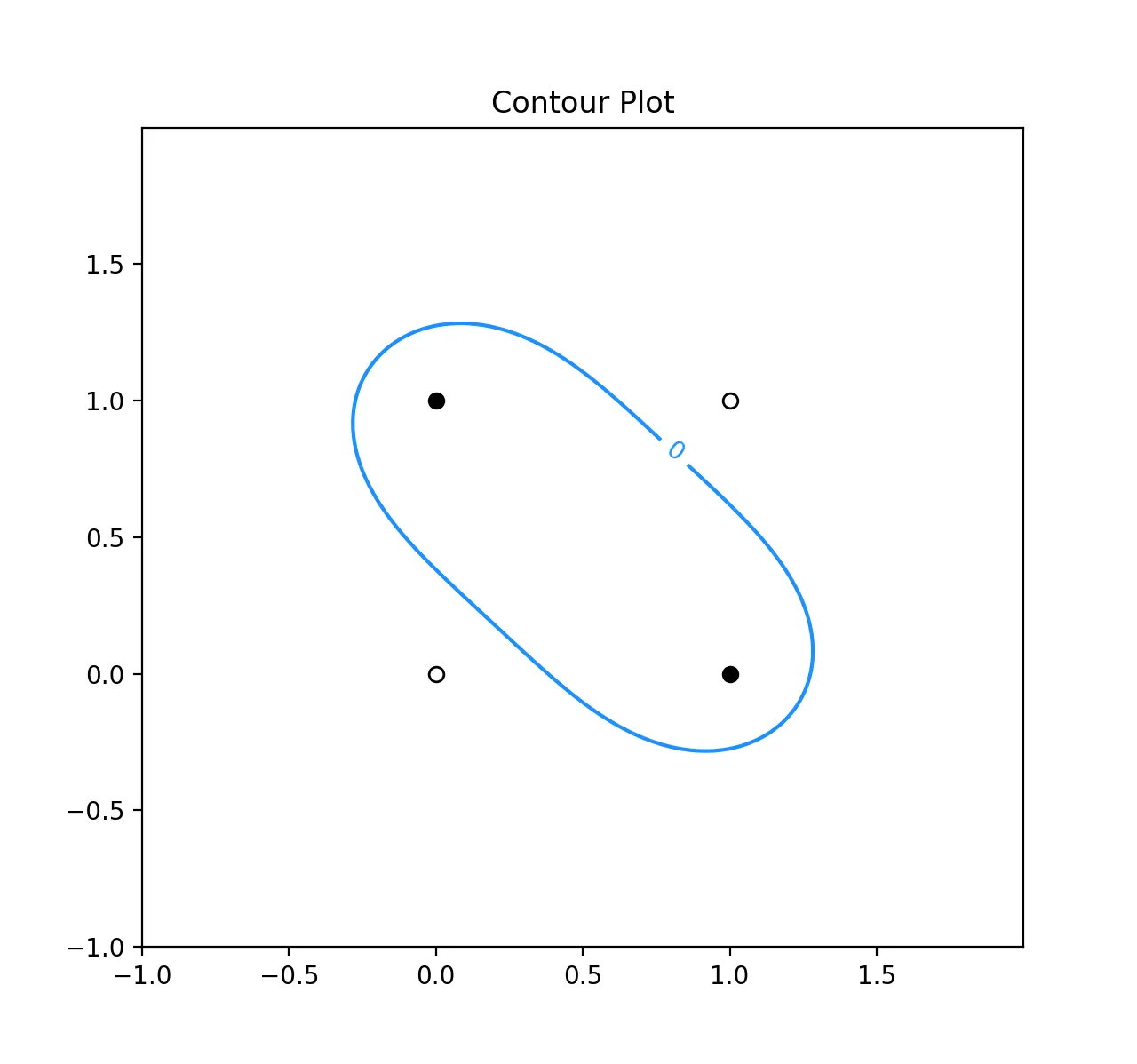
위와 같은 세팅으로 실제 Wx(i)+bWx^{(i)}+b = 0 을 기준으로 나누어 보면 다음과 같은 plot 이 나타납니다.
보시는 바와 같이, Wx(i)+bWx^{(i)}+b = 0 을 기준으로 안 쪽 범위가 0 보다 큰 범위로, 바깥 쪽 범위가 0 보다 작은 범위로 분리가 됩니다. 이 때 (0, 1), (1, 0) 은 contour 의 내부에 존재하여 1 값을, (0, 0), (1, 1) 은 contour 의 외부에 존재하여 0 값을 가지는 것을 실제로 확인할 수 있습니다.
여기까지 오시면, Radial Basis Function Network 가 무엇인지와 XOR 문제를 어떻게 해결하는지에 대해서 아실 것이라고 믿습니다. 이 시점에서 이런 의문들이 들 수 있습니다.
왜 수 많은 kernel 중에 Radial Basis Function Kernel 을 사용해야 하는 거지...? Kernel 의 피연산자가 될 vector 는 어떠한 기준으로 정해야 하는 거지...?
이 질문들에 대한 대답을 지금부터 해드리려고 합니다.
먼저, Radial Basis Function Kernel 을 사용하는 특별한 이유에 대해서 간단히 언급드리려고 합니다. 일반적인 kernel 같은 경우에는 mapping 하는 vector space 의 dimension 이 유한한데 비해, Radial Basis Function Kernel 은 mapping 하는 vector space 의 dimension 이 무한합니다. 이는 아래와 같이 간단하게 증명할 수 있습니다.
K(x,x′)=e−γ∥x−x′∥2=∏i=1dim(X)e−γ(xi−xi′)2=∏i=1dim(X)(e−xi2e−xi′2e2xixi′)γ=∏i=1dim(X)(e−xi2e−xi′2∑k=0∞2kxkx′kk!)γ=∏i=1dim(X)(e−xi2e−xi′2∑k=0∞2kxikxi′kk!)γ=∏i=1dim(X)(e−xi2e−xi′2(1,11!xi,12!xi2,13!xi3,...)⋅(1,11!xi′,12!xi′2,13!xi′3,...))γK(x,x')=e^{-\gamma\lVert x-x'\rVert^2}=\prod_{i=1}^{dim(X)}e^{-\gamma (x_i-x_i')^2}=\prod_{i=1}^{dim(X)}(e^{-x_i^2}e^{-x_i'^2}e^{2x_ix_i'})^{\gamma}\\ =\prod_{i=1}^{dim(X)}(e^{-x_i^2}e^{-x_i'^2}\sum_{k=0}^{\infin}\frac{2^kx^kx'^k}{k!})^{\gamma}=\prod_{i=1}^{dim(X)}(e^{-x_i^2}e^{-x_i'^2}\sum_{k=0}^{\infin}\frac{2^kx_i^kx_i'^k}{k!})^{\gamma}\\ =\prod_{i=1}^{dim(X)}(e^{-x_i^2}e^{-x_i'^2}(1, \sqrt{\frac{1}{1!}}x_i,\sqrt{\frac{1}{2!}}x_i^2,\sqrt{\frac{1}{3!}}x_i^3, ...)\cdot(1,\sqrt{\frac{1}{1!}}x_i',\sqrt{\frac{1}{2!}}x_i'^2,\sqrt{\frac{1}{3!}}x_i'^3, ...))^{\gamma}
위 식과 같이 product term 내부를 infinite dimension 의 inner product 형태로 만들 수 있고, product 할 때마다 각각의 항에 xix_i 관련 항목과 xi′x_i' 관련 항목을 나누어 곱하게 되면 product 를 풀더라도 결과적으로 inner product 형태로 나타낼 수 있음을 알 수 있습니다.
앞서 kernel 을 kernel trick 을 위해서 사용한다고 말씀드렸던 적이 있습니다. 이는 저차원의 데이터를 고차원으로 매핑시킨 뒤에 선형의 초평면으로 구별하기 위한 방법론이었습니다. 이 때 차원이 높을수록, 그 차원에서 선형적으로 표현할 수 있는 초평면의 범위가 넓어지게 되고, 복잡한 데이터도 구별할 수 있게 됩니다. 이러한 측면에서 무한 차원을 가진다는 점은 kernel trick 을 사용하는데에 굉장한 이점이 되는 것입니다.
다음으로 kernel 의 피연산자가 될 vector 를 설정하는 방법에 대해서 간단히 설명드리려고 합니다.
여기서 한 가지 짚고 넘어갈 점은, 실은 Radial Basis Function Network 에서 예시로 설명은 드렸지만 학습을 하지 않더라도 weight 를 정확하게 구해낼 수 있다는 점입니다. Radial Basis Function Network 의 경우에는 kernel 을 적용한 뒤에 ground-truth vector yy 와 mapping 을 거치고 산출된 vector φ(x)\varphi(x) 를 알고 있기 때문에 ΦW=y\varPhi W=y 식에서 Φ−1\varPhi^{-1} 을 양변의 앞에 곱해줌으로써 WW 를 직접적으로 구해낼 수 있습니다. 하지만, 이렇게 직접적으로 weight 를 구할 수 있음에도 Radial Basis Function Network 는 학습을 필요로 하는 네트워크입니다. Kernel 의 피연산자가 될 vector 값을 어느정도 유의미하게 산출할 때 학습이 필요한 것입니다. 앞에서는 reference vector 를 고정시키고 설명을 했지만, 실제로는 이 친구가 학습이 되는 parameter 이고, 이를 어느정도 학습을 통해 해를 구할 수 있을 정도로 찾아내면 이후에 이를 가지고 해를 직접적으로 구해낸다고 합니다. 물론, 이후에 vector 를 고정시키고 다시 학습하는 방법도 가능합니다.
이제 위의 궁금증들이 해결되었으리라 믿습니다.
이렇게 이번 세션에서는 Feed Forward(FF) 에 이어서 XOR 문제와 같은 복잡한 목적을 가지는 네트워크를 구현할 수 없었던 문제를 해결한 또 다른 네트워크인 Radial Basis Function Network 의 구조와 예시에 대해서 알아보는 시간을 가졌습니다. 이번 세션을 통해서 kernel 이 어떤 역할을 하는지, 그리고 Radial Basis Kernel 이 가지는 의미가 무엇인지에 대해서 알아두시면 좋을 것 같습니다.