Duplicate

Lecture 2 | Projective Geometry I

수강 일자
2023/02/21

Overview: Camera Projections

•
광원의 빛이 물체에 반사되어 카메라의 렌즈를 통과하여 CCD 센서에 도달하여 디지털 신호로 변환됨.
•
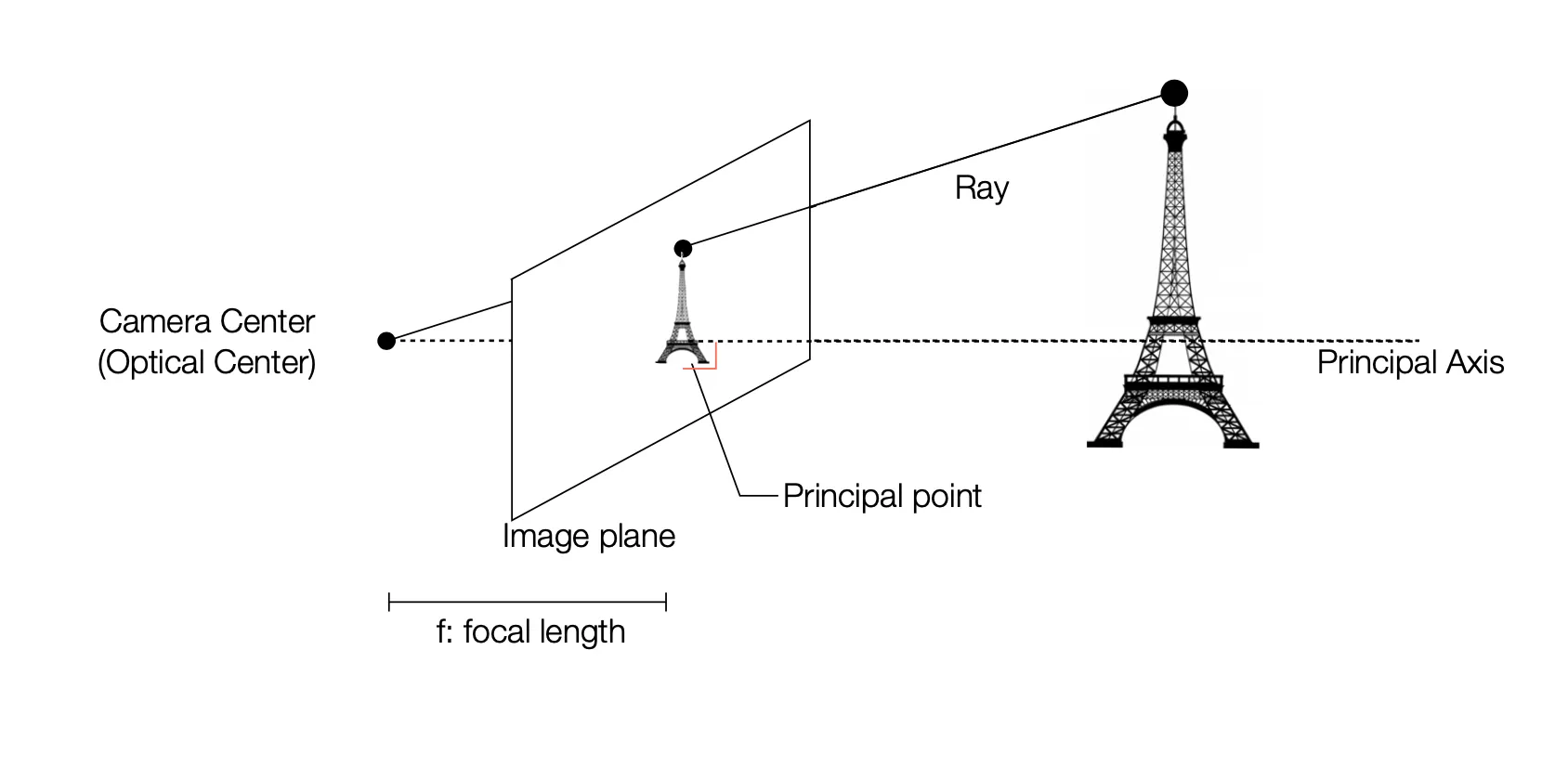
Camera System: Scene + Pinhole (Camera Center) + 2D Plane (Screen)
•
3D Projection (Capturing Scene) 은 3D Scene 을 2D Image 로 projection 하는 과정임.

What is Projective Transformations?

•
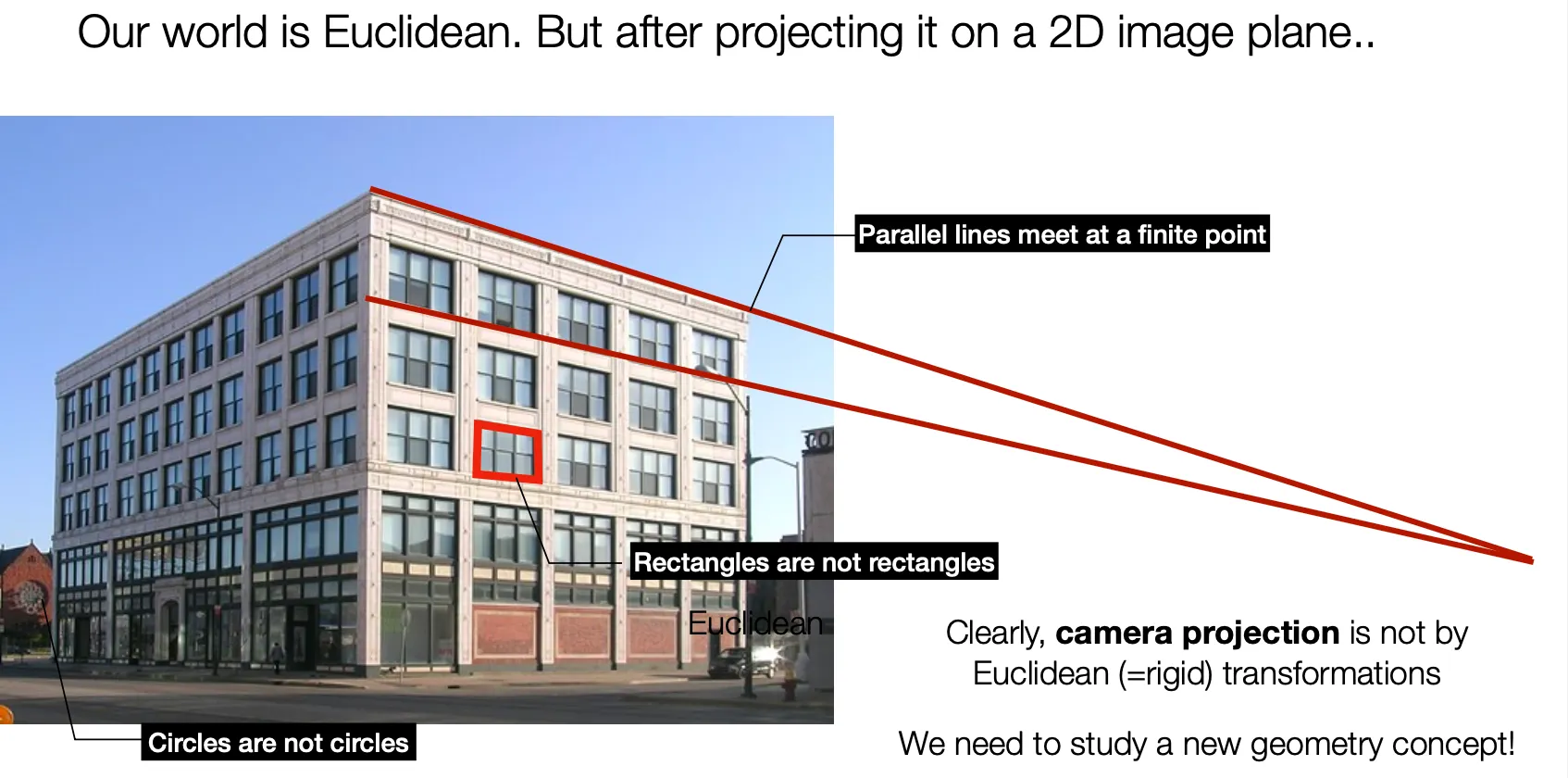
위 그림은 일반적인 이미지이지만, 다음과 같은 특이점이 있음.
◦
실제로는 평행한 선이 이미지 상에서는 평행하지 않고, 유한한 점에서 만남.
◦
실제로는 직사각형인 창문이 이미지 상에서는 평행사변형임.
◦
실제로는 원인 시계가 이미지 상에서는 타원임.

Euclidean Geometry ?! (RN)(\mathbb{R}^N)

•
3D Real World Space
•
세부적인 특징들 ?
◦
두 점 사이의 가장 가까운 거리는 직선임.
◦
삼각형의 내각의 크기의 합은 180°180\degree임.
◦
수직인 직선은 90°90\degree를 이룸.
◦
평행한 직선은 만나지 않음.
•
Euclidean Geometry 에서는 “Infinity” 가 정의될 수 없는 큰 단점이 있음!
◦
e.g. 평행한 두 선의 교점을 일반적인 방법과 동일하게 표현할 수 없음…

Projective Geometry !! (PN)(\mathbb{P}^N)

•
Euclidean + Infinity Points
•
세부적인 특징들 ?
◦
평행한 선이 유한한 점에서 만남. → Homogeneous Coordinate 로 확인할 수 있음.
◦
원이 타원으로 나타날 수 있음.
◦
직사각형이 평행사변형으로 나타날 수 있음.
◦
각, 길이, 길이의 비율이 유지되지 않음.

Representing A 2D Point in 2D Euclidean Space

•
Inhomogeneous Coordinate
x=(x1,x2)T=[x1x2]∈R2{\rm{x}} = (x_1,x_2)^T = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \in \mathbb{R}^2
•
Homogenenous Coordinate
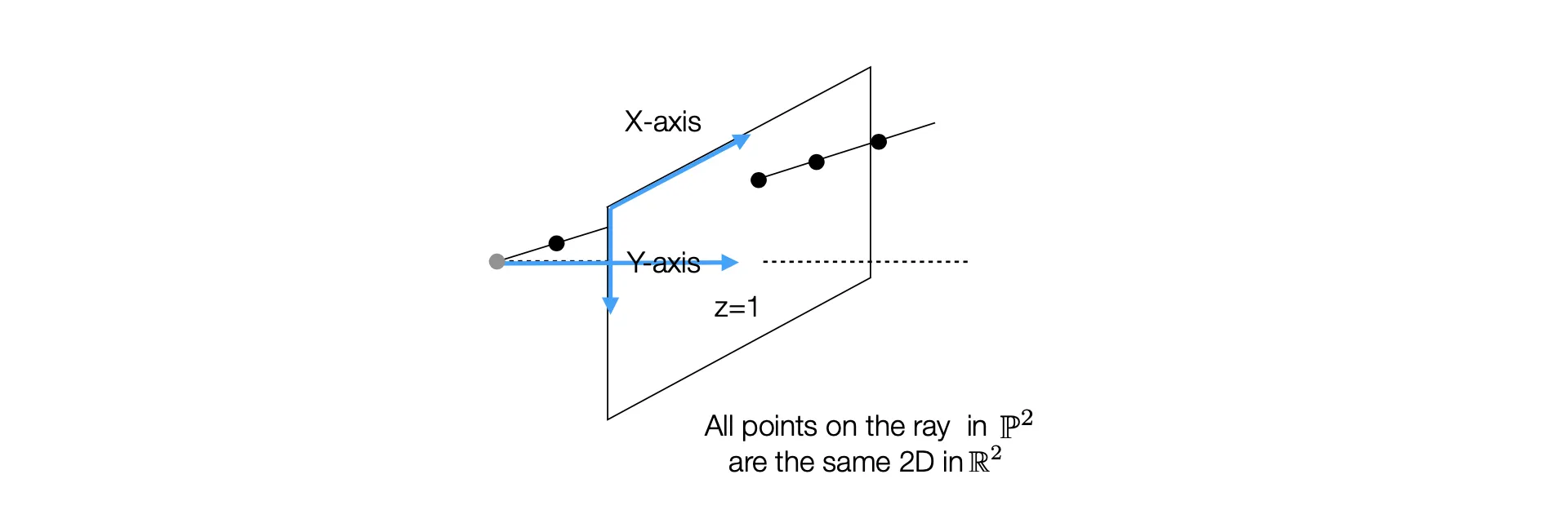
x=(x1,x2,1)T=[x1x21]=[kx1kx2k]∈P2{\rm{x}} = (x_1,x_2, 1)^T = \begin{bmatrix} x_1 \\ x_2 \\ 1 \end{bmatrix} = \begin{bmatrix} kx_1 \\ kx_2 \\ k \end{bmatrix} \in \mathbb{P}^2
◦
2D Euclidean Space 의 2D Point 를 3-dimensional vector 로 표현함.
◦
각 항목에 kk 가 곱해져도 같은 점을 의미함. (Up-To-Scale)
▪
마지막 차원의 1 은 z=1z=1 인 Image Plane 과 ray 와의 교점을 나머지 두 차원 (x1,x2)(x_1,x_2) 로 표현한 방식이기 때문에 주어짐.
▪
각 항목에 kk 가 곱해지는 것은 3차원 좌표 상에서는 Camera Center 로 이어지는 ray 상의 모든 점을 의미하지만, Homogeneous Coordinate 에서는 모두 같은 점 (Projected 2D Point) 을 의미함. → Homogeneous Coordinate 가 Projective Geometry 를 표현하는 이유임.
◦
(0,0,0)(0,0,0) 은 정의되지 않음.
P2=R3−{(0,0,0)}{\mathbb{P}^2} = {\mathbb{R}^3} - \{ (0,0,0)\}
◦
Inhomogeneous Coordinate 에서 표현할 수 없는 Infinity 는 하나의 차원이 추가된 “redundancy” 로 인해 Homogeneous Coordinate 에서 다음과 같이 표현할 수 있음. (Ideal Points)
[x1x20]\begin{bmatrix} x_1 \\ x_2 \\ 0 \end{bmatrix}
▪
Ideal Point 를 Inhomogeneous Coordinate 로 변환하기 위해서는 zero-division 을 거쳐야 하고, 의도했던 대로 Infinity 를 나타냄을 알 수 있음.

Representing A 2D Lines in Homogenous Coordinates

•
Inhomogeneous Coordinate 에서는 선은 다음과 같이 표현할 수 있음.
{(x1,x2)∣ax1+bx2+c=0}→[x1,x2,1][abc]=0\{(x_1,x_2)| ax_1+bx_2+c=0\} \to [x_1, x_2,1] \begin{bmatrix} a \\ b \\ c \end{bmatrix} = 0
•
Homogeneous Coordinate 에서 선은 다음과 같이 표현할 수 있음.
l=(a,b,c)T{\rm{l}} = (a,b,c)^T
◦
점과 동일하게 3차원으로 표현하지만, 선이라는 명시를 통해 선으로 해석할 수 있음.
◦
특정 선 l=(a,b,c)T{\rm{l}}=(a,b,c)^T 위의 점 xx 들은 다음과 같이 표현할 수 있음.
{x∣xTl=0}\{x | x^T\rm{l} =0\}
▪
재미있게도, xx 의 각 항에 kk 를 곱해도 식을 만족하며 (선 위에 있으며), 이는 Homogeneous Coordinate 에서도 비슷하게 보았던 특징임. 당연하게도, 3차원 상의 직선 위의 점들은 2차원 Plane 에 project 시켰을 때 동일한 점으로 간다는 사실을 수식으로도 확인할 수 있는 부분임.
◦
특정 선 l=(a,b,c)T{\rm l}=(a,b,c)^T 에 대해 normal vector n{\rm n} 은 다음 관계가 성립함.
l=(a,b,c)T=(nx,ny,d)T=(n,d)T∥n∥2=1{\rm l}=(a,b,c)^T = (n_x, n_y, d)^T =({\rm n}, d)^T \quad {\|n\|}_2=1
▪
기존 Euclidean Space 에서의 normal (a,b,c)(a,b,c) 를 zz 에 대해 projection 시키면 (a,b)(a,b) 가 normal vector 의 방향임을 알 수 있고, normalize 시키면 됨.

Degree of Freedom (DoF)

•
Independent Variable 의 수
•
일반적으로 3D 벡터는 3DoF 를 가지지만, Homogenous Coordinate 에서는 2DoF 를 가짐.
◦
세 항의 비율이 같은 벡터는 동일한 벡터이기 때문임. (Up-To-Scale)

Cross Product and Skew-Symmetric Matrix

•
일반적인 Cross Product 는 다음과 같음.
a×b=(a2b3−a3b2a3b1−a1b3a1b2−a2b1)a\times b = \begin{pmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{pmatrix}
•
위 Cross Product 를 Matrix Multiplication 형태로 표현할 수 있음.
a×b=[a]×b=[0−a3a2a30−a1−a2a10](b1b2b3)=(a2b3−a3b2a3b1−a1b3a1b2−a2b1)a\times b = [a]_{\times}b = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} =\begin{pmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{pmatrix}
◦
Matrix Multiplication 을 사용하면 다른 Matrix 연산과 합치기도 용이하고, 병렬처리 등이 간편함.
•
Skew Symmetrix Matrix 는 AT=−AA^T = -A 를 만족하는 matrix 임. → 앞선 [a]×[a]_{\times} 가 Skew Symmetric !

The Line Joining Two Points

•
Homogeneous Coordinate 에서 두 점을 지나는 직선은 다음과 같이 나타낼 수 있음.
l=x×x′=[x]×x′{\rm l} = {\rm x}\times {\rm x'} = [{\rm x}]_{\times} x'
◦
l⋅x=lTx=(x×x′)Tx=0{\rm l} \cdot {\rm x} = {\rm l}^T{\rm x} = ({\rm x} \times {\rm x'})^T {\rm x} = 0 이고, l⋅x′=lTx′=(x×x′)Tx′=0{\rm l} \cdot {\rm x'} = {\rm l}^T{\rm x'} = ({\rm x} \times {\rm x'})^T {\rm x'} = 0 이기 때문에 x,x′{\rm x}, {\rm x'} 는 모두 l{\rm l} 이 실제 3차원 공간에서 표현하는 선 위에 있음을 보일 수 있음.

Intersection of Lines

•
Homogeneous Coordinate 에서 두 선의 교점은 다음과 같이 나타낼 수 있음.
x=l×l′=[l]×l′{\rm x} = {\rm l} \times {\rm l}' = [\rm l]_{\times} {\rm l}'
◦
l⋅x=lTx=lT(l×l′)=0{\rm l}\cdot {\rm x} = {\rm l}^T {\rm x} = {\rm l}^T({\rm l} \times {\rm l'}) = 0 이고, l′⋅x=l′Tx=l′T(l×l′)=0{\rm l'}\cdot {\rm x} = {\rm l'}^T {\rm x} = {\rm l'}^T({\rm l} \times {\rm l'}) = 0 이기 때문에 x{\rm x} 는 l{\rm l} 과 l′{\rm l'} 에 동시에 위에 있음을 보일 수 있음.

Intersection of Two Parallel Lines

l=(−1,0,1)Tl′=(−1,0,2)T{\rm l } = (-1, 0, 1)^T \\ {\rm l' } = (-1, 0, 2)^T \\
•
두 직선의 교점은 앞선 설명과 같이 l×l′{\rm l} \times {\rm l}' 로 계산할 수 있음.
l×l′=(0,1,0)T{\rm l} \times {\rm l'} = (0, 1, 0)^T
◦
교점이 Ideal Point (Infinity) 에 있음을 확인할 수 있음. (Last element is zero !)
•
신기한 점은, yy 축에 평행한 직선 (−1,0,c)T(-1, 0, c)^T 는 모두 동일한 점 (0,1,0)T(0,1,0)^T 에서 만난다는 점임.
◦
(−1,0,c)T(0,1,0)=0(-1,0,c)^T(0,1,0) = 0 이기 때문에 해당 점이 해당 선 위에 있음.
◦
마찬가지로, xx 축에 평행한 직선은 모두 동일한 점 (1,0,0)T(1, 0, 0)^T 에서 만남.