Duplicate

Lecture 16 | Unsupervised Learning

형태
Machine Learning
수강 일자
2022/10/26

Recap: Eigenvalues and Eigenvectors

•
Square Matrix AA 의 eigenvector 는 다음을 만족하는 nonzero vector vv 로 정의함.
Av=λvAv=\lambda v
•
이 때 λ\lambda 가 해당 eigenvector 에 대응되는 eigenvalue
•
vv 가 eignvector 이면 rescaled vector svsv 도 eigenvector 가 되기 때문에 eigenvector 의 크기를 1 로 정의함. (∥v∥2=1\| v \|_2 =1)

Recap: Singular Value Decomposition (SVD)

•
m×nm\times n matrix AA 에 대해서 SVD 는 다음과 같이 factorization 됨.
A=UΣVTA=U\Sigma V^T
◦
UU 는 m×mm\times m orthonormal matrix (column 이 eigenvector)
◦
VTV^T는 n×nn\times n orthonormal matrix (row 가 eigenvector)
◦
Σ\Sigma 는 m×nm\times n diagonal matrix (σ1≥σ2≥σ3...\sigma_1 \ge \sigma_2 \ge \sigma_3 ...)

Relation between SVD and Eigenvalue Decomposition

•
A=UΣVTA=U\Sigma V^T 라고 할 때, ATAA^TA 는 다음과 같음.
ATA=(UΣVT)T(UΣVT)=VΣTUTUΣVT=VΣTΣVT=VΣ2VT\begin{align*} A^TA &= (U\Sigma V^T)^T(U\Sigma V^T) \\ &=V\Sigma^TU^TU\Sigma V^T \\ &=V\Sigma^T\Sigma V^T \\ &= V\Sigma^2 V^T \end{align*}
◦
Σ2\Sigma^2 는 n×nn\times n vector 로, nn 개까지의 eigenvalue 의 제곱이 각 대각성분에 있는 matrix 임. (나머지는 0 으로 채워짐)
◦
마찬가지로, AAT=UΣ2UTAA^T=U\Sigma^2 U^T 이고, 여기서의 Σ2\Sigma^2 는 m×mm\times m 임.
◦
즉, UU 와 VV 는 각각 AATAA^T, ATAA^TA 의 eigenvector 로 구성된 matrix 임.
◦
AATAA^T, ATAA^TA 의 eigenvalue 는 singularvalue 의 제곱임. (Σ2\Sigma^2 가 eigenvalue decomposition 의 diagnoal matrix 가 되기 때문!)

Variance

•
var[f]=E((f(x)−E[f(x)])2]{\rm var}[f] = {\mathbb{E}}((f(x)-{\mathbb{E}}[f(x)])^2]
•
var[f]=E[f(x)2]−E[f(x)]2{\rm var}[f] = {\mathbb{E}}[f(x)^2]-{\mathbb{E}}[f(x)]^2
•
var[x]=E[x2]−E[x]2{\rm var}[x] = {\mathbb{E}}[x^2]-{\mathbb{E}}[x]^2
•
제곱의 평균 - 평균의 제곱

Covariances

•
cov[x,y]=Ex,y[{x−E[x]}{y−E[y]}]=Ex,y[xy]−E[x]E[y] {\rm cov}[x,y] = {\mathbb{E}}_{x,y}[\{x-\mathbb{E}[x]\}\{y-\mathbb{E}[y] \}] = {\mathbb{E}}_{x,y}[xy]-{\mathbb{E}}[x]{\mathbb{E}}[y]
•
cov[x,y]=Ex,y[{x−E[x]}{yT−E[yT]}]=Ex,y[xyT]−E[x]E[yT] {\rm cov}[\rm x,y] = {\mathbb{E}}_{x,y}[\{x-\mathbb{E}[x]\}\{y^T-\mathbb{E}[y^T] \}] = {\mathbb{E}}_{x,y}[xy^T]-{\mathbb{E}}[x]{\mathbb{E}}[y^T]
◦
Covariance Matrix 과 다름!
◦
x∈Rmx\in R^m, y∈Rny\in R^n → cov[x,y]∈Rm×n{\rm cov[x,y]} \in R^{m\times n}
•
Covariance Matrix 는 Symmetric 하고 Positive Semidefinite
M=E[(x−E[x])(x−E[x])T]uTMu=uTE[(x−E[x])(x−E[x])T]u=E[uT(x−E[x])(x−E[x])Tu]=E[uT(x−E[x])((x−E[x])uT)T]≥0M ={\mathbb{E}}[(x-{\mathbb{E}}[x])(x-{\mathbb{E}}[x])^T]\\ \begin{align*} u^TMu &= u^T{\mathbb{E}}[(x-{\mathbb{E}}[x])(x-{\mathbb{E}}[x])^T]u\\ &= {\mathbb{E}}[u^T(x-{\mathbb{E}}[x])(x-{\mathbb{E}}[x])^Tu]\\ &= {\mathbb{E}}[u^T(x-{\mathbb{E}}[x])((x-{\mathbb{E}}[x])u^T)^T]\\ &\ge 0 \end{align*}

Principal Component Analysis (PCA)

•
높은 차원의 데이터를 유의미한 것만 남기고 차원을 줄일 수 있는 방법론
•
가장 정보를 많이 잃지 않으면서 차원을 낮추는 방법 → Variation 이 가장 큰 방향으로의 Projection
•
uu 방향으로의 projection 을 가정했을 때 projection 후의 variance? (∥u∥2=1\| u \|_2 = 1)
1n∑i(xiTu)2=1n∑iuTxixiTu=uT(1n∑ixixiT)uC=1n∑ixixiT→variance of n dimensional  zeromean vectors\begin{align*} \frac{1}{n}\sum_i (x_i^Tu)^2 &= \frac{1}{n}\sum_i u^Tx_ix_i^Tu \\ &= u^T(\frac{1}{n}\sum_i x_ix_i^T)u \end{align*}\\ C=\frac{1}{n}\sum_i x_ix_i^T \rarr {\rm variance\ of\ n\ dimensional\ \ zeromean\ vectors}
•
해당 variance 를 크게 하는 uu 는 eigenvector of largest eigenvalue of CC
maximize    uTCu       subject to  ∥u∥2=1↔maximize    L(u,λ)=uTCu+λ(1−uTu) (Lagrange Multiplier)2Cu−λ′u=0→Cu=λuuTCu=uT(Cu)=uTλu=λuTu=λ\begin{align*} &{\rm maximize}\thickspace\thickspace u^TCu\ \thickspace\thickspace\thickspace {\rm subject\ to} \thickspace \| u \|_2 = 1 \lrarr \\ &{\rm maximize}\thickspace\thickspace L(u,\lambda) = u^TCu + \lambda(1-u^Tu)\ ({\rm Lagrange\ Multiplier})\\ & 2Cu-\lambda'u =0\rarr Cu=\lambda u \\ &u^TCu = u^T(Cu) = u^T\lambda u=\lambda u^Tu = \lambda \end{align*}
◦
최대값을 만드는 uu 의 후보군은 CC 의 eigenvector
◦
eigenvector uu 에 대해 uTCuu^TCu 는 eigenvalue λ\lambda 를 가지고, 최댓값은 최대 eigenvalue
◦
variance 를 가장 크게 만드는 uu 는 가장 큰 eigenvalue 를 가지는 eigenvector
◦
C=XXTC=XX^T 형태이므로 X=UΣVTX=U\Sigma V^T 로 SVD 를 적용한 뒤에 UU 의 largest singular vector 를 찾는 것과 같음…!
•
PCA 를 통해서 variance 를 기준으로 변경된 차원들의 축은 각 eigenvector 이며, N 개의 차원을 줄이고 싶다면 가장 작은 eigenvalue 를 가지는 N 개의 eigenvector 를 제거하면 됨! (축 제거)

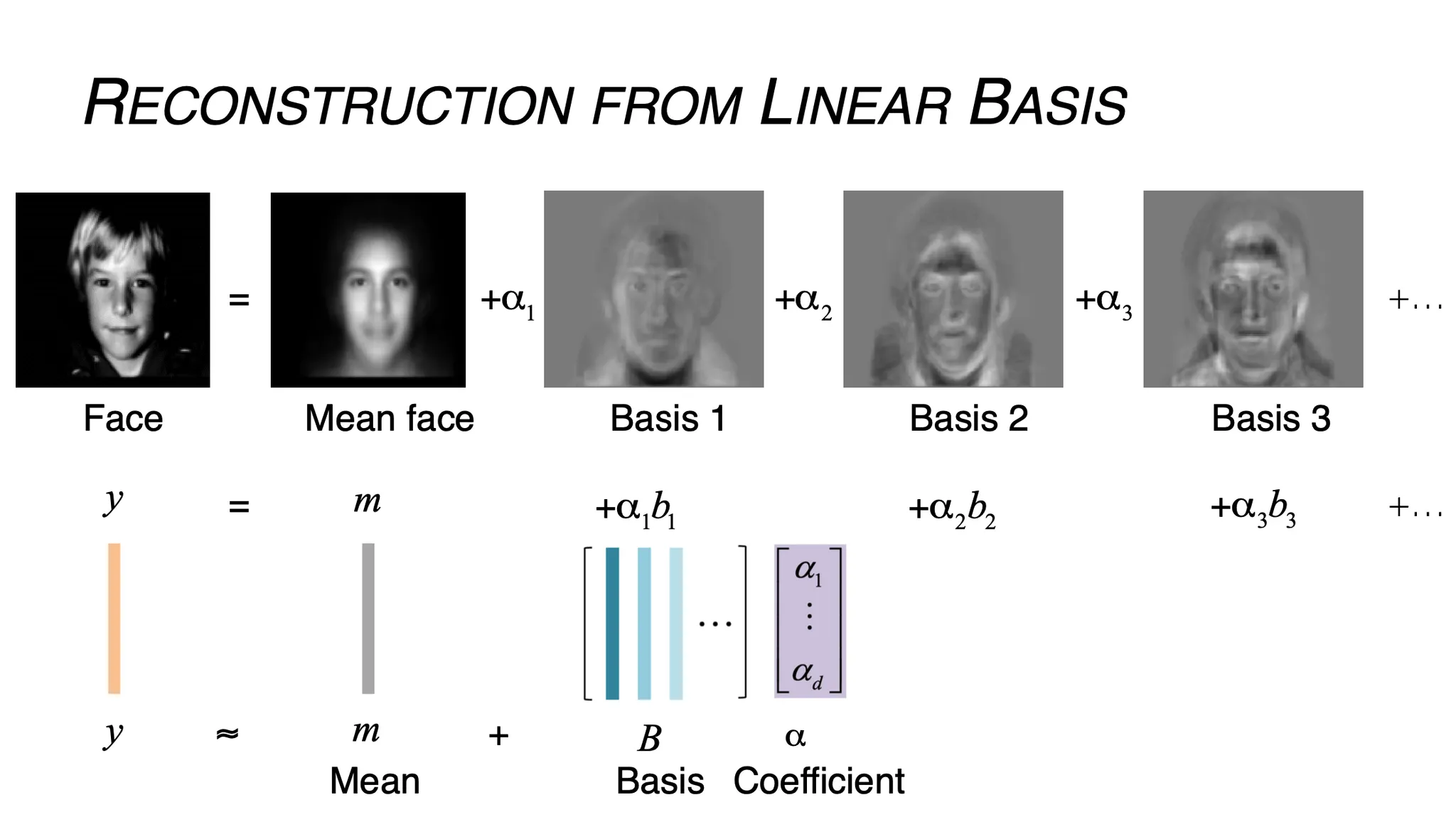
Additional: EigenFaces

•
256×256256\times 256 의 얼굴 이미지는 각 픽셀마다 차원을 가지기 때문에 차원이 굉장히 높음.
•
이 차원을 낮추면 mean 과 적은 수의 basis 로 얼굴을 재구성할 수 있음!
•
3D Face, Body 또한 마찬가지로 Low Dimension 으로 표현할 수 있음! (Mean Shape + Shape + Motion, Mean Shape + Shape Variation + Body Pose)

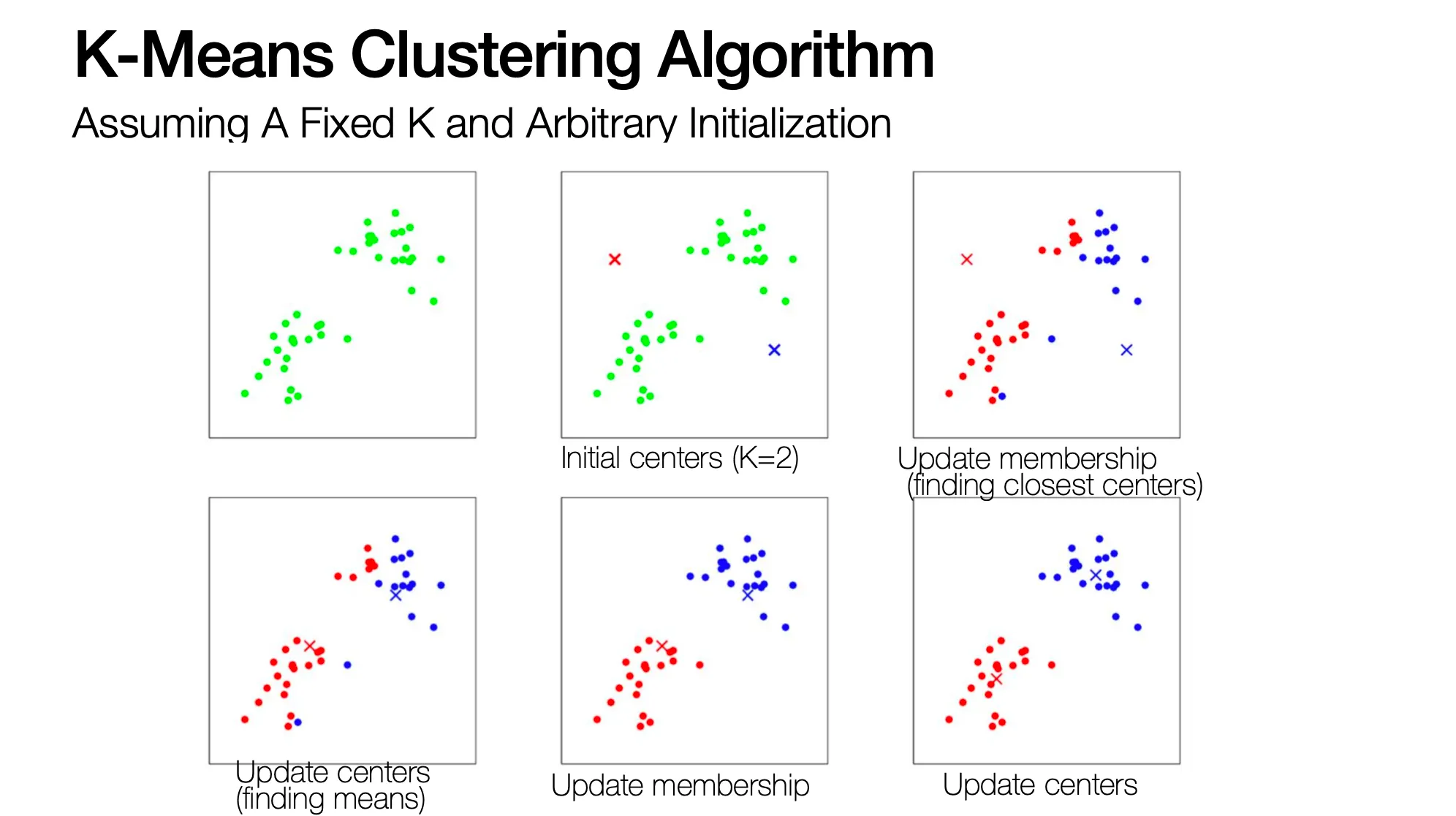
K-means Clustering

•
Clustering 의 목표는 각 그룹의 center 를 찾는 것
•
특정 데이터마다 속한 그룹 (membership) 이 정해지면, 가장 좋은 cluster center 는 각 그룹에 속한 데이터와 그 그룹의 center 와의 거리가 최소인 clustering 임.
SSD=∑iK∑x∈Ci(x−ci)2{\rm SSD} = \sum_i^K\sum_{x\in C_i}(x-c_i)^2
◦
위 식은 Sum of Squared Distance 로 거리를 설정한 것
•
Membership 까지 변수로 고려한 최종적인 clustering 의 목적 함수는 다음과 같음!
c∗,δ∗=arg min⁡c,δ∑jN∑iKδij(xj−ci)2c^*, \delta^* = \argmin_{c,\delta}\sum_j^N\sum_i^K \delta_{ij}(x_j-c_i)^2
◦
δij\delta_{ij} 는 cluster ii 에 데이터 xjx_j 가 속하는지의 여부를 나타냄. 속하면 1, 아니면 0.
•
K-Means Clustering 은 초기에 cluster center (μ1,μ2,...μk∈Rd\mu_1,\mu_2,...\mu_k \in {\mathbb R}^d)를 임의로 둔 후,
1.
각 데이터들 각각에 대해서 가장 가까운 center 로 membership 을 설정함.
ci:arg min⁡j∥xi−μj∥2c_i:\argmin_j \|x_i-\mu_j\|^2
2.
동일한 membership 들을 가지는 데이터의 중심으로 해당 membership 의 center 를 옮김
μj:=∑i=1n1{ci=j}xi∑i=1n1{ci=j}\mu_j:=\frac{\sum_{i=1}^n 1\{c_i=j\}x_i}{\sum_{i=1}^n 1\{c_i=j\}}
◦
위의 1~2 를 convergence 까지 반복함! (반복해도 데이터의 membership 이 바뀌지 않을 때까지-)
•
픽셀들의 color 데이터로 clustering 을 할 수도 있음..! (동일한 색상이 동일한 cluster)
•
“K 를 어떻게 설정해야 하는가” 가 K-Means Clustering 의 가장 큰 한계점
•
“Initial centroid 를 어떻게 설정해야 하는가” 도 다른 문제점임 → 최대한 다양한 시작점을 둠!
•
Distance measure 또한 SSD 가 아니라 다르게 할 수 있음!

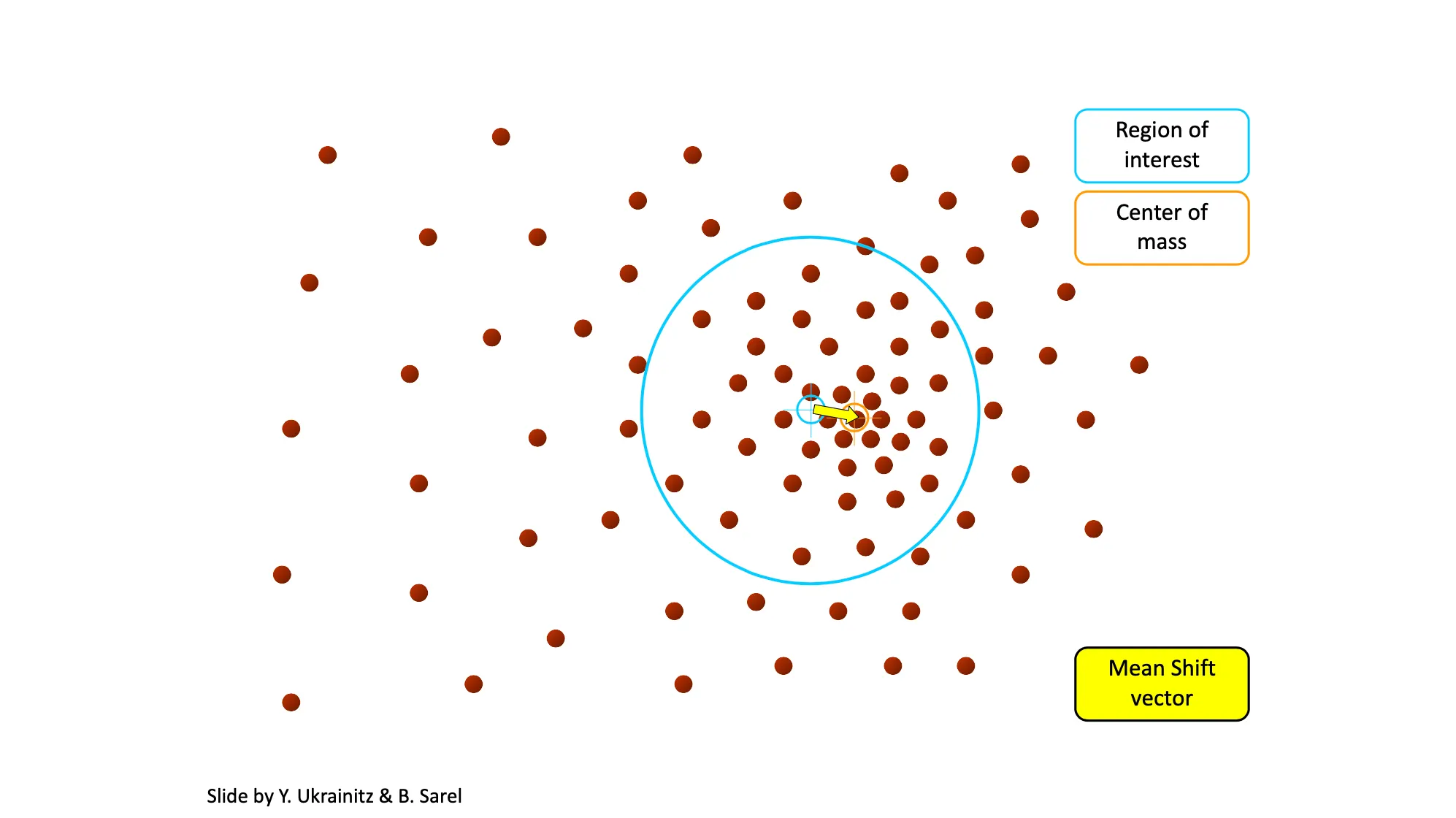
Mean-Shift

•
K-Means Clustering 은 초기 시작점에 대한 정보 없이 랜덤하게 설정해야 하는 문제점이 있음.
•
Mean-Shift 는 다음과 같은 알고리즘으로 진행됨.
1.
임의의 시작 위치와 window size 를 설정
2.
해당 Window Size 에 속한 데이터들의 중심으로 window 의 중심을 옮김
3.
2번을 반복함!
•
Cluster 는 동일한 데이터 지점으로 모일 수 있는 시작점들의 영역 (Attraction Basin) 내에 속한 데이터들을 묶으면 됨.
•
K 값을 정할 필요가 없지만, window size 를 정할 필요가 있음.