Duplicate

Lecture 12 | Two View Geometry II

수강 일자
2023/03/01

Projective Ambiguity of Cameras Given F{\rm F}

•
Camera Projection Matrix P,P′P, P' 가 주어지면 F{\rm F} 를 유일하게 결정할 수 있음.
◦
하지만 반대로, F{\rm F} 가 주어졌을 때 P,P′P, P' 을 유일하게 결정할 수 없음. 이는 각 Camera Projection Matrix 에 4×44\times 4 Projective Transformation H{\rm H} 를 곱해도 동일한 F{\rm F} 를 얻을 수 있기 때문임.
F=[e′]×P′P+P,P′→FPH,P′H→F{\rm F} = [e']_{\times}P'P^+ \\ \quad \\ P, P' \to {\rm F} \\ PH, P'H \to {\rm F}
◦
정성적으로는 PP 에는 World Coordinate → Camera Coordinate 로 변경하는 과정이 포함되어 있고, World Coordinate 를 어떻게 택하느냐에 따라서 같은 F{\rm F} 를 가지는 Epipolar Geometry System 이라도 다양한 P,P′P, P' 의 조합이 나올 수 있음.

Canonical Forms of Camera Metrices

•
일반성을 잃지 않고 두 Camera Projection Matrix 를 다음과 같이 표현할 수 있음.
P=[I∣0]P′=[M∣m]P=[I|0] \quad P'=[M| m]
•
Fundamental Matrix F{\rm F} 는 다음과 같이 표현됨.
F=[m]×M{\rm F} =[m]_{\times}M
◦
이는 다음과 같이 유도할 수 있음.
e′=P′C=[M∣m][0,0,0,1]T=mF=[e′]×P′P+=[m]×[M∣m][I3×303×1]=[m]×M e'=P'C=[M|m][0,0,0,1]^T = m \\ F =[e']_{\times}P'P^+ = [m]_{\times}[M|m] \begin{bmatrix} I_{3\times 3} \\ 0_{3\times 1} \end{bmatrix} =[m]_{\times}M

Skew Symmetric Matrix

A=−ATA=-A^T
•
3D Cross Product 는 다음과 같은 Skew Symmetric Matrix 의 Left Multiplication 으로 변형 가능함.
[e]×=[0−ϵ3ϵ2ϵ30−ϵ1−ϵ2ϵ10][e]_{\times} = \begin{bmatrix} 0 & -\epsilon_3 & \epsilon_2 \\ \epsilon_3 & 0 & -\epsilon_1 \\ -\epsilon_2 & \epsilon_1 & 0 \\ \end{bmatrix}
•
Skew Symmetric Matrix 는 다음과 같이 Block Diagonal Form 으로 표현할 수 있음.
A=UDUTwhere D=[0−λ0λ00000]A = UDU^T \\ {\rm where}\ D = \begin{bmatrix} 0 & -\lambda & 0 \\ \lambda & 0& 0 \\ 0 & 0 & 0 \\ \end{bmatrix}
•
Skew Symmetric 은 다음과 같은 특성도 가지고 있음.
xTAx=0,∀x↔A is skew-symmetricx^TAx = 0, \forall x \lrarr A\ {\rm is\ skew{\text -} symmetric}
1.
If AA is skew-symmetric
A=−ATxTAx=(xTAx)T=xTATx=−xTAx→xTAx=0,∀xA = -A^T \\ x^TAx = (x^TAx)^T =x^TA^Tx = -x^TAx \to x^TAx=0, \forall x
2.
If xTAx=0,∀xx^TAx = 0, \forall x
eiTAei=0→Aii=0(ei+ej)TA(ei+ej)=0→Aij+Aji=0→A=−ATe_i^TAe_i = 0 \to A_{ii}=0 \\ (e_i+e_j)^TA(e_i+e_j) = 0 \to A_{ij} + A_{ji} = 0 \\ \quad \\ \to A=-A^T
•
e1=[1,0,0]T,e2=[0,1,0]T,…e_1 = [1, 0,0]^T, e_2 =[0, 1, 0]^T , \dots

Canonical Cameras Given F{\rm F}: When F{\rm F} be a Fundamental Matrix?

F is the Fundamental Matrix with P,P′↔P′TFP is skew-symmetric{\rm F\ is\ the\ Fundamental\ Matrix\ with\ } P, P' \lrarr P'^T{\rm F}P \ {\rm is\ skew{\text -}symmetric}
•
P,P′P, P' 에 대해 정의된 F{\rm F} 가 Fundamental Matrix 임은 P′TFPP'^T{\rm F}P 가 Skew Symmetric 인 것과 동치임.
P′TFP is skew-symmetric↔XT(P′TFP)X=0,∀X↔(XTP′T)F(PX)=0,∀X↔x′TFx=0,∀X↔F is the Fundamental Matrix\begin{align*} P'^T{\rm F}P \ {\rm is\ skew{\text -}symmetric} &\lrarr X^T(P'^T{\rm F}P)X=0, \forall X \\ &\lrarr (X^TP'^T){\rm F}(PX)=0, \forall X \\ &\lrarr x'^T{\rm F}x=0, \forall X \\ &\lrarr {\rm F\ is\ the\ Fundamental\ Matrix} \end{align*}

Canonical Cameras Given F{\rm F}: Decomposing F{\rm F} into a Camera Pair

P=[I∣0]P′=[SF∣e′]P=[I|0] \quad P'=[S{\rm F}|e']
•
F{\rm F} 가 주어졌을 때 두 Camera Projection Matrix P,P′P, P' 을 위와 같이 decomposition 할 수 있음.
◦
SS 는 임의의 Rank 3 의 Skew Symmetric Matrix 임. → 유효한 P′P' 을 위한 조건임.
◦
e′e' 은 e′F=0e'{\rm F}=0 을 만족하는 Epipole 임.
•
P′TFPP'^T{\rm F}P 가 Skew Symmetric 임을 통해 F{\rm F} 가 Fundamental Matrix 임을 보일 수 있음.
[SF∣e′]TF[I∣0]=[FTSTF0e′F0]=[FTSTF000][S{\rm F}|e']^TF[I|0] = \begin{bmatrix} {\rm F}^TS^T{\rm F} & 0 \\ e'{\rm F} & 0 \end{bmatrix} = \begin{bmatrix} {\rm F}^TS^T{\rm F} & 0 \\ 0 & 0 \end{bmatrix}
◦
SS 가 Skew Symmetric 이었기 때문에 위 식도 Skew Symmetric 이고 증명할 수 있음.
•
SS 에 대한 안전한 해는 S=[e′]×S=[e']_{\times} 임. 이는 이러한 세팅이 P′P' 의 Rank 3 가 보장되기 때문임.
P=[I∣0]P′=[[e′]×F∣e′]P=[I|0] \quad P' = [[e']_{\times}{\rm F}|e']

Essential Matrix EE

•
KK 를 알고 있는 Calibrated Case 에서는 특별하게 Coordinate 를 바꿔서 생각해볼 수 있음.
x=K[R∣t]X→K−1x=[R∣t]Xx^=K−1xx = K[R| {\rm t}]X \to K^{-1}x = [R| {\rm t}]X \\ \hat{x} = K^{-1}x
◦
x^{\hat x} 를 Normalized Coordinate 라고 함.
•
Normalized Coordinate 에서는 P,P′P,P' 을 KK 없이 간단하게 다음과 같이 나타낼 수 있음.
P=[I∣0]P′=[R∣t]P=[I|0]\quad P'=[R|{\rm t}]
•
기존의 Fundamental Matrix 의 constraint 식은 다음과 같이 변형될 수 있음.
F=K′−T[t]×RK−1x′TFx=0x′TK′−T[t]×RK−1x=0→x′^T[t]×Rx^=0→x′^TEx^=0where E=[t]×R{\rm F} = K'^{-T}[{\rm t}]_{\times}RK^{-1}\quad x'^T{\rm F}x =0 \quad \\ x'^TK'^{-T}[{\rm t}]_{\times}RK^{-1}x = 0 \to \hat{x'}^T[{\rm t}]_{\times}R\hat{x} = 0 \\ \to \hat{x'}^TE\hat{x} = 0 \quad {\rm where}\ E =[{\rm t}]_{\times}R
◦
새로운 EE 를 위와 같이 정의할 수 있고, Fundamental Matrix 와 E=K′TFKE = K'^T{\rm F}K 의 관계를 가짐.
◦
[t][\rm t] 가 Rank 2 이고, RR 이 Full Rank 이기 때문에 EE 는 Rank 2 임.
◦
EE 는 [t][\rm t] 가 3DoF, RR 이 3DoF 인데 Up-to-Scale 이어서 5DoF 를 가짐.

Properties of Essential Matrix

•
Essential Matrix 를 SVD 하면, 다음과 같은 형태가 됨.
E=U[λ000λ0000]VTE=U \begin{bmatrix} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0& 0 & 0\\ \end{bmatrix}V^T
◦
이 강의에서 증명은 하지 않음.

Extracting Cameras from Essential Matrix

•
앞선 SVD 의 특징들을 이용하여 EE 로부터 R,tR, {\rm t} 를 추출할 수 있음.
E=[t]×R=U[λ000λ0000]VTE=[{\rm t}]_{\times}R =U\begin{bmatrix} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0& 0 & 0\\ \end{bmatrix}V^T
◦
위 식에서 가운데 항을 다음과 같이 Up-to-Scale 을 고려해 decomposition 할 수 있음.
[λ000λ0000]=ZXZ=[010−100000]W=[0−10100001]X=W or WT\begin{bmatrix} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0& 0 & 0\\ \end{bmatrix} = ZX \\ Z = \begin{bmatrix} 0 & 1 & 0 \\ -1 & 0& 0 \\ 0& 0 & 0\\ \end{bmatrix} \quad W= \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0& 0 \\ 0& 0 & 1\\ \end{bmatrix} \quad X = W \ {\rm or}\ W^T
◦
E=U(ZX)VT=(UZUT)(UXVT)E = U(ZX)V^T = (UZU^T)(UXV^T) 로 변형이 가능함.
[t]×=UZUTR=UXVT[{\rm t}]_{\times} = UZU^T \\ R = UXV^T
▪
UZUTUZU^T 가 Skew Symmetric Matrix 의 Block Diagnoal Form 형태임을 통해 [t]×[{\rm t}]_{\times} 로 지정할 수 있음.
▪
XX 가 orthogonality 에 영향을 주지 않음을 통해 전체 UXVTUXV^T 가 orthogonal 하고 detdet 가 1임을 통해 UXVTUXV^T 를 RR 로 지정할 수 있음.
•
특별한 점은 F{\rm F} 에서 Camera Parameters 를 얻어내는 경우와는 달리 EE 에서 얻어내는 것은 4 개의 possible solution 이 있어 상대적으로 ambiguity 가 적음.
t=±u3R=UWVT or UWTVT{\rm t} = \pm {\rm u}_3 \\ R = UWV^T\ {\rm or}\ UW^TV^T
◦
구해낸 R,tR, {\rm t} 로부터 다시 P,P′P,P' 을 복원할 수 있음.
P=[I∣0]P′=[UWVT∣u3] or [UWVT∣−u3] or [UWTVT∣u3] or [UWTVT∣−u3]P =[I|0] \\ P' = [UWV^T | {\rm u}_3]\ {\rm or}\ [UWV^T | -{\rm u}_3]\ {\rm or}\ [UW^TV^T | {\rm u}_3]\ {\rm or}\ [UW^TV^T | -{\rm u}_3]
◦
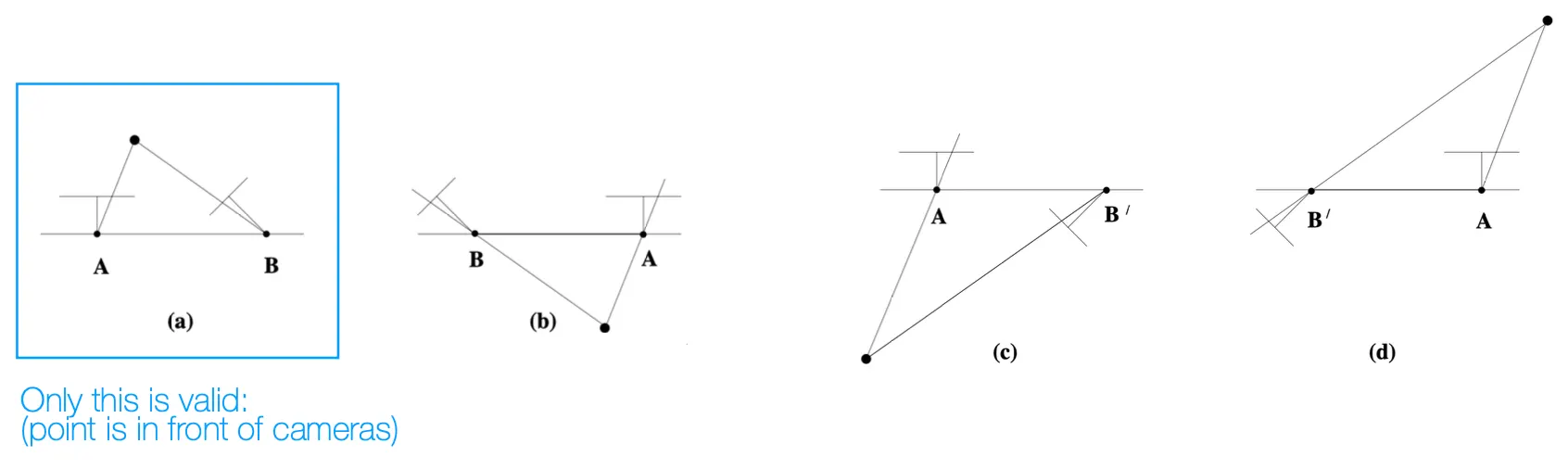
위 네 가지의 solution 중 아래의 (a)(a) 가 가장 적합한 경우임.

Estimating Fundamental Matrix F{\rm F}: 8 Points Algorithm

•
x′TFx=0x'^T{\rm F}x = 0 을 만족하는 대응점 쌍 x=(x,y,1)T,x′=(x′,y′,1)Tx = (x,y,1)^T, x'=(x',y',1)^T 를 이용해서 F{\rm F} 를 역으로 계산해낼 수 있음.
x′xf11+x′yf12+x′f13+y′xf21+y′yf22+y′f23+xf31+yf32+f33=0→(x′x,x′y,x′,y′x,y′y,y′,x,y,1)f=0→Af=0x'xf_{11} + x'yf_{12}+x'f_{13}+y'xf_{21}+y'yf_{22} + y'f_{23} + xf_{31} + yf_{32}+f_{33} = 0 \\ \to (x'x, x'y, x', y'x, y'y,y',x, y,1){\rm f} = 0 \\ \to Af = 0
•
f{\rm f} 는 9 개의 variable 을 가지고 있고 Up-to-Scale 이기 때문에 8 개의 Corresponding Points 를 가지고 있으면 f{\rm f} 를 specify 할 수 있음. (8 Points Algorithm)
◦
하지만 이렇게 구하면 실제로는 7DoF 인 F{\rm F} 가 추가적인 constraint 가 없기 때문에 Rank 2 가 아닐 수도 있음.
•
이 문제를 해결하기 위해 Singularity Constraint 를 추가하여 다음과 같은 처리를 할 수 있음.
F=UDVT→F′=UD′VTF=UDV^T \to F'=UD'V^T
◦
D′D' 은 DD 의 가장 작은 singular value 를 0 으로 만든 diagonal matrix 임.
◦
이렇게 계산된 F′F' 은 det(F′)=0det(F') = 0 조건을 만족하면서 FF 와의 Frobenius Norm 을 최소화하는 값이기도 함.
•
Practical 한 case 에 실제 Corresponding Points 의 좌표가 너무 크거나 분포가 어려우면, noise 가 극대화될 수도 있기에 center origin + RMS distance 2\sqrt2 등의 방법으로 normalization 을 거친 후에 DLT 로 F^\hat{\rm F} 를 먼저 계산하고 나중에 denormalize 를 함.

Estimating Fundamental Matrix F{\rm F}: 7 Points Algorithm

•
8 Points 로 시작하여 Singularity Constraint 를 추가하지 말고, 애초부터 7 Points 만으로 F{\rm F} 를 계산할 수 있는 방법론 (7DoF 인 F{\rm F} 를 예측하기 위해 필요한 최소의 Corresponding Points 만을 이용)
•
7 Points 만을 이용해서 Af=0A{\rm f} = 0 의 문제를 해결하면 dimension 이 2 인 Null Space 를 구할 수 있고, 최종적인 해는 다음과 같은 형태로 나타나게 됨.
F=(1−λ)F1+λF2{\rm F} = (1-\lambda){\rm F}_1 + \lambda{\rm F}_2
◦
Null Space 의 basis 가 f1,f2f_1, f_2 이고 이것이 나타내는 Fundamental Matrix 가 각각 F1,F2F_1, F_2 임.
•
위에서 구한 일반해에 det(F)=0det({\rm F}) =0 의 constraint 를 사용할 수 있음. (Rank 2 이기 때문임)
◦
λ\lambda 에 대한 3차식의 해로 λ\lambda 를 구해낼 수 있기 때문에 1개, 혹은 3개의 가능한 해를 얻어낼 수 있음.

Estimating Essential Matrix EE: 5 Points Algorithm

•
5DoF 인 EE 를 구하기 위해서 5 개의 Corresponding Points 가 필요함.
•
구체적으로는 다루지 않음.