Duplicate

Lecture 19 | Stereo

수강 일자
2023/03/07

Local Feature Matching

•
Intereset Point Extractor
◦
서로 다른 두 이미지에서 동일하게 나타나는 (Repeatable) 한 point 를 찾음.
•
Descriptor
◦
찾은 Interest Point 가 matching 되는지 아닌지 확인하기 위한 feature 를 추출하는 과정
◦
Scale, Rotation, Illumination 과 같은 효과를 제거한, 순수 feature 만을 뽑는 것이 중요함.
◦
두 점의 descriptor 가 비슷하면 대응되는 점으로 봄. 다만, RANSAC 등으로 인해서 많은 Sparse 한 Interesting Point 만이 존재하기 때문에 대응점들의 수가 적은 편임 → SfM 의 결과가 sparse 한 주요한 이유임…!

Dense 3D Reconstruction

•
SfM 의 sparsity 를 해결하기 위해서 Dense 3D Reconstruction 을 고려해볼 수 있음.
•
이를 위해 1차적으로 depth estimation 을 진행할 수 있음.
◦
depth 가 작으면 (거리가 가까우면) disparity (이미지 상 거리 변화) 가 큼. → disparity 기반으로 depth 를 예측할 수 있음.

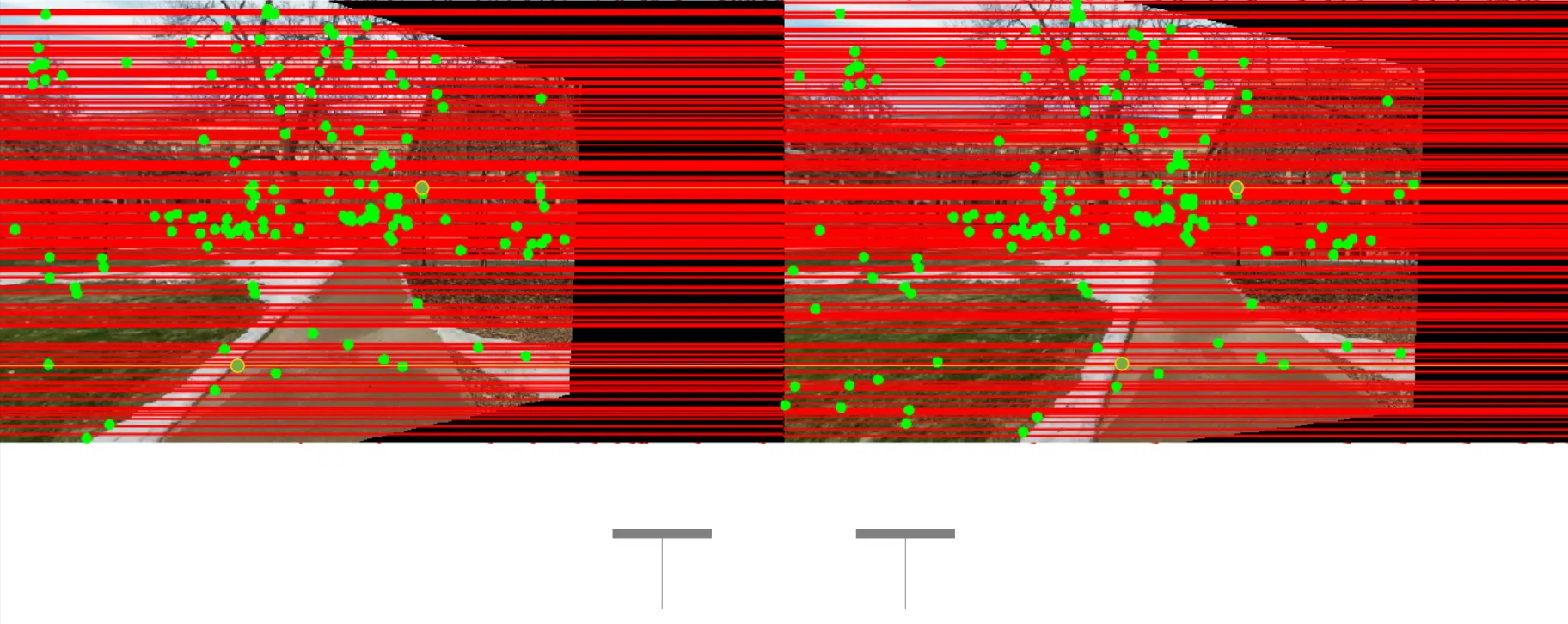
Rectifying Images for Easier Stereo Matching

•
Pure Rotation 을 적용하여 camera 를 평행하게 바꾸어 rectify 를 진행하고 epipolar line 을 horizontal 하게 변경할 수 있음.
◦
두 이미지 상이 평행하기 때문에 R=IR=I
◦
두 이미지 상이 평행하므로 baseline 이 서로의 이미지를 지나지 않으며 epipole e′e' 은 point at infinity 인 (1,0,0)T(1,0,0)^T 로 나타낼 수 있음.
F=[e′]×K′RK−1=[e′]×KK−1=[e′]×=[00000−1010]x′Fx=0→y=y′F=[e']_{\times}K'RK^{-1} = [e']_{\times}KK^{-1} = [e']_{\times} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix} \\ {\rm x}'F{\rm x} = 0 \to y=y'
◦
이렇게 만들기 위해서 Pure Rotation 을 적용하되, epipole 을 (1,0,0)T(1,0,0)^T 로 보내는 Homography 를 구하면 됨. (Pure Rotation 으로 충분한 이유…? → 동일한 KK 가정에 t{\rm t} 는 FF 계산에 필요가 없기 때문인듯 함…)
•
이렇게 변경하면, horizontal line 에서 corresponding point 를 찾으면 되고, disparity 를 찾기 쉬워짐

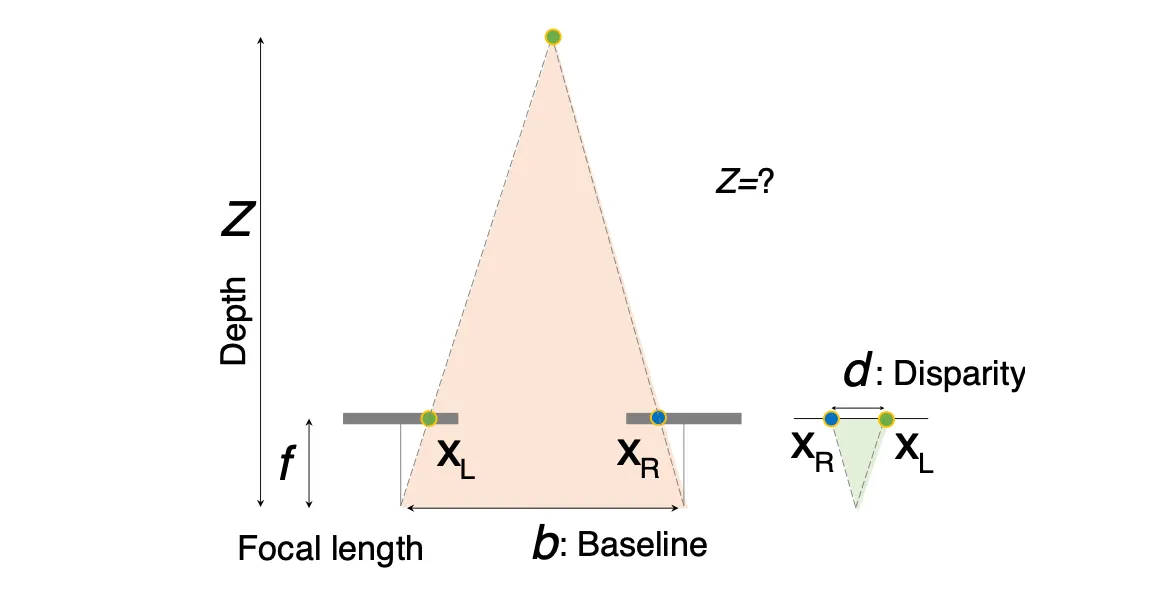
Disparity vs. Depth

Zb=fd→Z=bfd\frac{Z}{b} = \frac{f}{d} \to Z = b\frac{f}{d}
•
Depth 는 Dispartiy 에 반비례함.
•
Depth 가 주어지면, Disparity 는 Baseline 길이에 비례함.
◦
Depth 를 잘 알기 위해서는 Baseline 이 크면 좋음. (disparity 차이가 극명하게 나기 때문임)
◦
근데 또, Baseline 이 크면 point matching 이 어려움…

Stereo Matching

•
동일한 horizontal line 위에서 matching 지점을 찾아 그 pixel 차이를 disparity 로 지정함.
•
다만 matching 을 찾는 방법에 여러가지 방법이 있음.
1.
SAD (Sum of Absolute Differences
SAD(k,l)=∑(i,j)∈T∣El(i,j)−Er(i+k,j+l)∣SAD(k,l) = \sum_{(i,j) \in T}|E_l(i,j)-E_r(i+k,j+l)|
•
특정 지점의 patch ElE_l 를 이용하여 k,lk,l 만큼 이동시킨 위치에 같은 크기만큼의 patch 와의 L1 norm 을 구하는 방식
2.
SSD (Sum of Squared Differences)
SSD(k,l)=∑(i,j)∈T∣El(i,j)−Er(i+k,j+l)∣2SSD(k,l) = \sum_{(i,j) \in T}|E_l(i,j)-E_r(i+k,j+l)|^2
•
SAD 의 L2 norm 버전
3.
NCC (Normalized Cross-Correlation)
NCC(k,l)=∑(i,j)∈TEl(i,j)Er(i+k,j+l)∑(i,j)∈TEl(i,j)2∑(i,j)∈TEr(i+k,j+l)2NCC(k,l) = \frac{\sum_{(i,j)\in T}E_l(i,j)E_r(i+k,j+l)}{\sqrt{\sum_{(i,j) \in T}E_l(i,j)^2\sum_{(i,j)\in T}E_r(i+k,j+l)^2}}
Template Matching
•
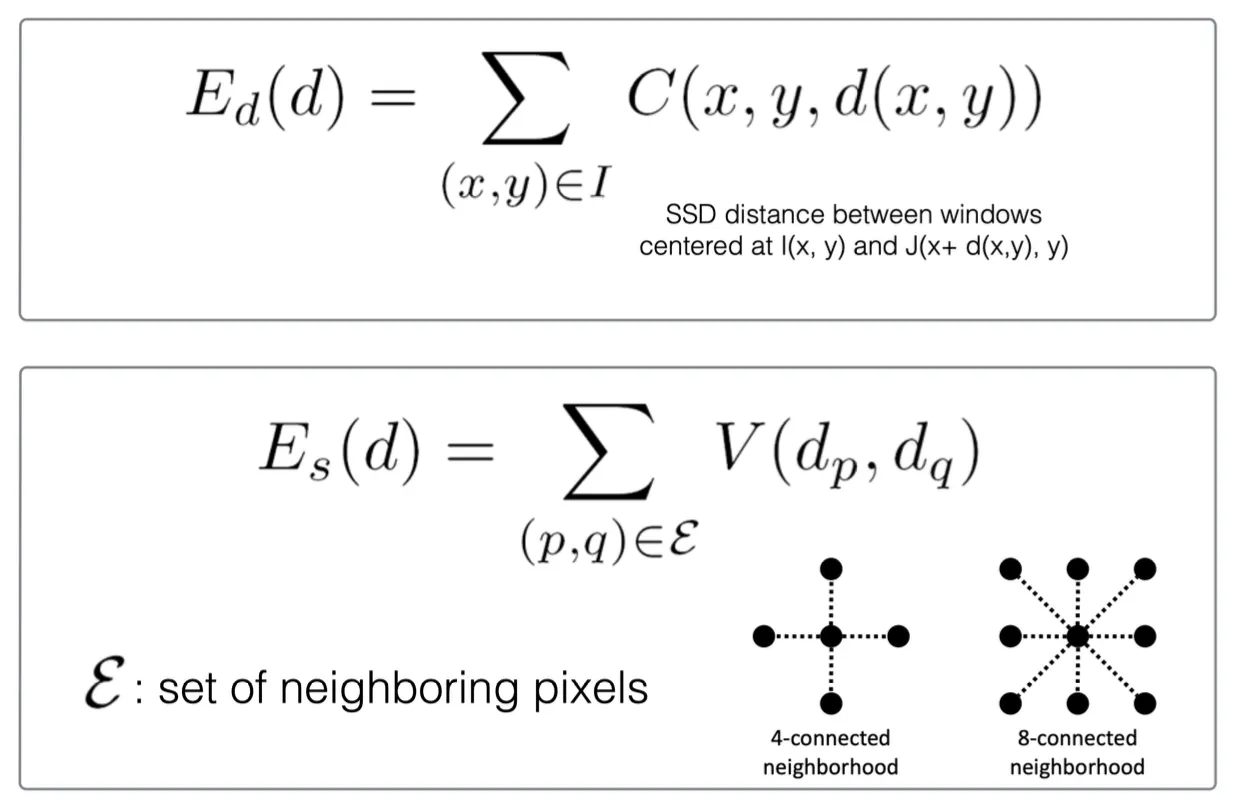
SSD 의 식은 다음과 같음.
E[i,j]=∑m∑n(f[m,n]−t[m−i,n−j])2→E[i,j]=∑m∑n(f2[m,n]+t2[m−i,n−j]−2f[m,n]t[m−i,n−j])E[i,j] =\sum_m\sum_n (f[m,n]-t[m-i,n-j])^2 \\ \to E[i,j] =\sum_m\sum_n (f^2[m,n] + t^2[m-i,n-j]-2f[m,n]t[m-i,n-j])
•
위의 식을 최소화하는 것은 제일 마지막 term 을 최대화하는 것과 어느정도는 일맥상통함. (Template 은 고정되어 있지만, (i,j)(i,j) 의 변화에 따라 t[m−i,n−j]t[m-i,n-j] 가 변하기 때문임…)
•
이 항목을 Cross-Correlation 이라고 부름
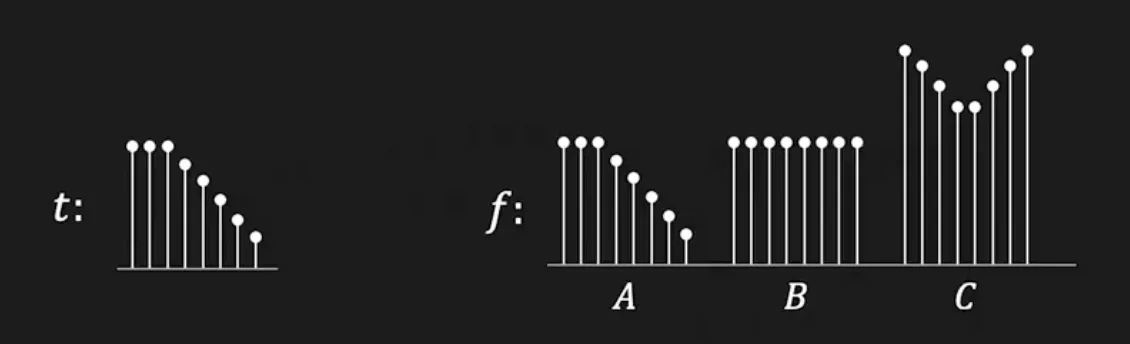
Rtf[i,j]=∑m∑nf[m,n]t[m−i,n−j]R_{tf}[i,j] = \sum_m\sum_n f[m,n]t[m-i,n-j]
•
다만 위 항목은 그냥 무조건 곱해지는 값이 크면 클수록 분포나 패턴와 관계없이 커지는 이상한 값임.
◦
아래 그림에서 Rtf(C)>Rtf(B)>Rtf(A)R_{tf}(C) > R_{tf}(B) > R_{tf}(A)
•
때문에 비교 전 각 값들을 normalize 하여 사용할 수 있으며, Normalized Cross Correlation 이라고 함.
Ntf(i,j)=∑m∑nf[m,n]t[m−i,n−j]∑m∑nf2[m,n]∑m∑nt[m−i,n−j]N_{tf}(i,j) = \frac{\sum_{m}\sum_n f[m,n]t[m-i,n-j]}{\sqrt{\sum_{m}\sum_nf^2[m,n]}\sqrt{\sum_{m}\sum_n t^[m-i,n-j]}}
◦
이 값은 Illumination 에도 robust 하게 동작하기 때문에 template matching 의 좋은 baseline 임.

Template Matching: Window Size Matters

•
Window size 가 작으면 디테일을 챙길 수 있지만, 노이즈가 있을 수 있음.
•
반대로, window size 가 크면 노이즈는 제거할 수 있지만, 디테일을 챙길 수 없었음.

When Will Stereo Block Matching Fail?

•
Textureless Regions → Matching 이 잘 안됨.
•
Repeated Patterns → Matching 이 햇갈려할 수 있음.
•
Specularities → 유리나 거울같은 재질에서 다르게 보이는 경우… Matching 이 잘 안됨.
•
이런 것들을 해결하기 위해 Smoothness Constraints 를 도입함.
◦
Neighboring 픽셀은 disparity 가 비슷해야 한다는 constraints 를 추가함.

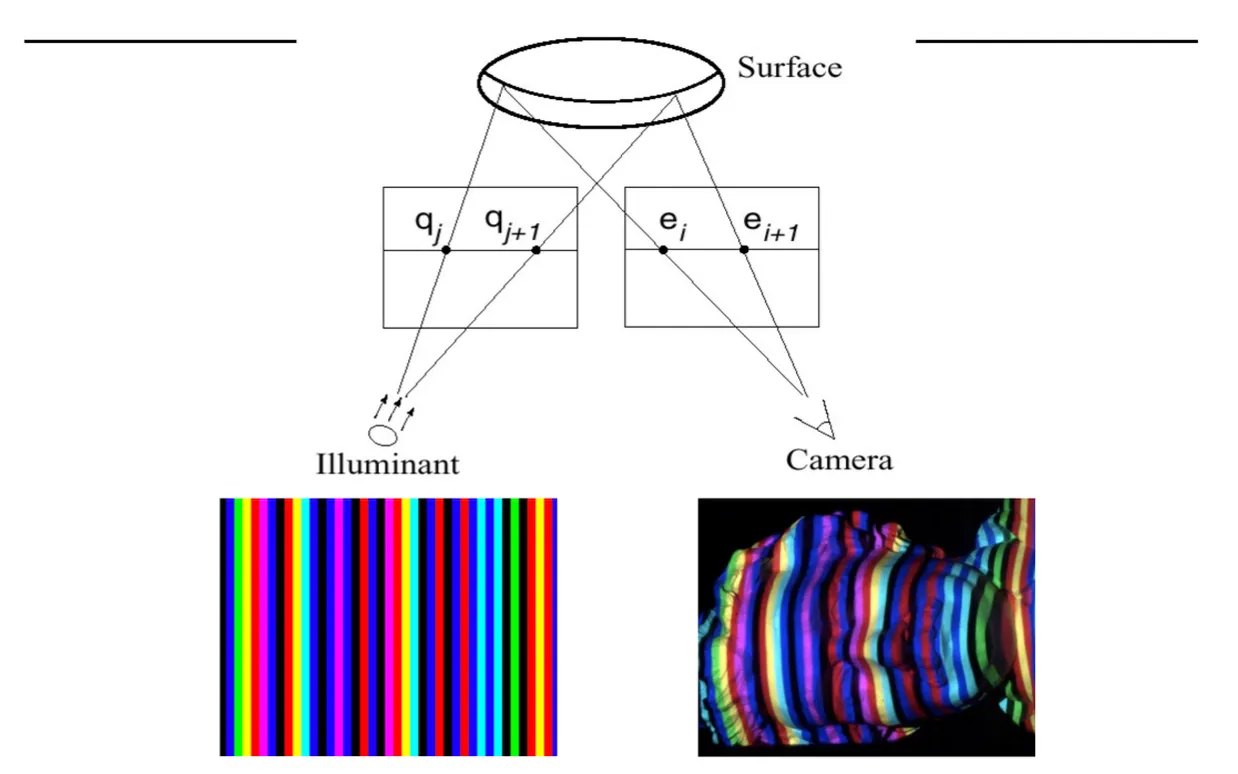
Active Stereo with Structured Light

•
두 카메라가 아닌 하나는 Structured Pattern 이 존재하는 빛을 쏘는 projector 로 대체함.
◦
두 카메라랑 완전히 동일한 세팅인데, 한 가지 장점은 projector 는 control 이 가능하다는 점임.
◦
이는 textureless 와 같은 단점을 극복할 수 있음.
•
재밌는 점은 이게 상용화가 됨… (Kinect)
◦
IR ray 를 쏘는 projector 와 IR camera 가 달린 기계로 Active Stereo 를 구성함.
◦
이 방법의 장점은 실시간 disparity 를 구할 수 있다는 것임.
◦
근데 또 IR ray 다 보니 태양이 있는 환경에서는 동작하지 않음. → Kinect 2 는 time of flight 개념을 사용함.